La corrente elettrica è una grandezza fisica scalare che rende conto di un flusso di carica elettrica all’interno di un materiale.
Se in un intervallo di tempo di durata $ \Delta t $ si registra il passaggio di una carica elettrica $ \Delta q $, definiamo l’intensità di corrente elettrica come $$ i = \frac{ \Delta q }{ \Delta t } $$L’unità di misura della corrente elettrica può essere dedotta dalla sua definizione: nel sistema internazionale, siccome la carica elettrica viene misurata in Coulomb $\text{C}$ e il tempo viene misurato in secondi $\text{s}$, l’unità di misura della corrente elettrica è $\frac{1 \text{ C} }{1 \text{ s}}$, e prende il nome di Ampere, in simboli $\text{A}$; per una corrente di $1 \text{ A}$, si registra il passaggio di una carica di $1 \text{ C}$ in un intervallo di tempo della durata di $1 \text{ s}$.
La corrente elettrica tuttavia necessita di un presupposto fondamentale: il movimento di carica elettrica.
Come sappiamo, le cariche elettriche interagiscono tra loro secondo la legge di Coulomb, e cariche soggette a un campo elettrico $\vec{E}$ sono soggette a una forza $\vec{F} = q \vec{E}$. Ma esistono cariche elettriche libere di muoversi, e dunque di generare corrente elettrica? Una classe di materiali è definita proprio da questa proprietà: si tratta dei materiali conduttori.
In un materiale conduttore sono presenti degli elettroni detti, appunto, di conduzione, liberi di muoversi tra gli orbitali più esterni degli atomi che compongono il materiale. In un regime di equilibrio elettrostatico, cioè in assenza di una differenza di potenziale elettrico, il moto di questi elettroni è mediamente nullo (in realtà, si muovono di moto caotico: tuttavia la loro velocità media è nulla, il che significa che, complessivamente, essi non si muovono lungo una direzione preferita, ma uniformemente lungo ogni direzione). Applicando una differenza di potenziale $\Delta V$, gli elettroni vengono accelerati dal conseguente campo elettrico: se la differenza di potenziale è applicata a due punti distanti $d$, gli elettroni saranno soggetti ad una forza pari a $$ \vec{F} = - q \frac{\Delta V}{d} $$

La carica $q$ è quella di un elettrone, ed è pari a $ -e = - 1.602 \cdot 10^{-19} \text{ C} $; il segno “$-$” è una conseguenza della convenzione sui segni delle cariche, e per questo motivo gli elettroni si spostano da zone in cui il potenziale elettrico è minore verso regioni a potenziale più alto; il verso è opposto a quello della corrente elettrica, come tra l’altro si può evincere dalla definizione stessa di corrente: infatti, in presenza di una carica negativa, si ha una corrente negativa.
Un tratto di materiale conduttore che formi un percorso chiuso si dice circuito elettrico.
Si presti attenzione, tuttavia, che la corrente elettrica, dovuta al moto dei singoli elettroni, non è il moto degli elettroni di conduzione. Per un cavo conduttore della sezione di $1 \text{ mm}^2$ attraversato da una corrente di $1 \text{ A}$, supponendo una densità di elettroni di conduzione di circa $10^{28}$ elettroni al metro cubo, si ottiene una velocità media di $10^{-3}\ \ \frac{\text{m}}{\text{s}}$, ma sperimentalmente si verifica che la corrente elettrica si manifesta quasi istantaneamente in tutti i punti del conduttore; questo è dovuto al fatto che, mentre gli elettroni di conduzione sono “lenti”, il campo elettrico, responsabile del loro moto e, in ultima analisi, della corrente elettrica, si propaga nel conduttore con una velocità comparabile a quella della luce.
Ad ogni modo, elettroni messi moto da una differenza di potenziale $\Delta V$ generano una corrente elettrica di intensità $i$. Ma qual è la relazione che sussite tra queste due grandezze fisiche? Agli inizi del 1800, lo scienziato tedesco Georg Simon Ohm, eseguì numerosi esperimenti a riguardo e arrivò ad affermare la sua famosa legge. Spesso detta anche prima legge di Ohm, essa afferma che, in regime stazionario (condizione che si ottiene imponendo che, complessivamente, la carica elettrica non cambi, ossia che la corrente elettrica sia mantenuta costante), il rapporto tra differenza di potenziale $\Delta V$ e intensità di corrente $i$ è di proporzionalità diretta. La costante di proporzionalità diretta si chiama resistenza, identificata dal simbolo $R$, ed esprimibile secondo la formula $$ \Delta V = R \ i $$
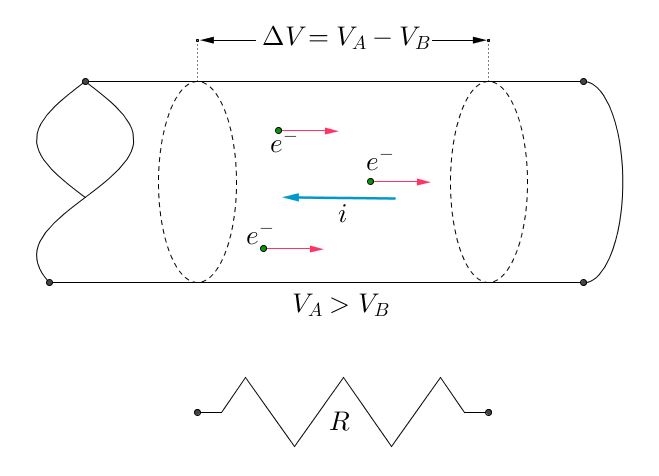
L’unità di misura della resistenza, in onore di colui che ha enunciato per primo questa legge, è l’Ohm, indicato dal simbolo $\Omega$, e una resistenza di un Ohm vale $1 \ \Omega = \frac{1 \text{ V}}{1 \text{ A}}$
Per un tratto di materiale conduttore filiforme, di lunghezza $l$ e sezione $S$, si verifica sperimentalmente che la resistenza $R$ di tale tratto è direttamente proporzionale alla lunghezza $l$ del tratto stesso e inversamente proporzionale alla sezione $S$: vale infatti la relazione $$ R = \rho \frac{l}{S} $$ove il simbolo $\rho$ (la rho dell’alfabeto greco) indica una grandezza nota come reisistività, ossia la resistenza per metro di lunghezza al metro quadro di area della sezione. Questa relazione va spesso sotto il nome di seconda legge di Ohm. La resistività dipende dal materiale attraverso cui scorre la corrente (in realtà dipende anche da altri parametri, primo tra tutti la temperatura), e si misura, nel sistema internazionale, in Ohm al metro $\Omega \text{ m}$. Di seguito indichiamo i valori per la resistività di alcuni materiali
| Materiali conduttori | Resistività in $\Omega \text{ m}$ (a $20^° \text{ C}$) |
Materiali isolanti | Resistività in $\Omega \text{ m}$ (a $20^° \text{ C}$) |
|
Alluminio |
$2.82 \cdot 10^{-8}$ | Acqua (distillata) | $0.5 \cdot 10^{6}$ |
| Argento | $1.62 \cdot 10^{-8}$ | Alcool Etilico | $0.26 \cdot 10^{5}$ |
| Costantana | $44 \cdot 10^{-8}$ | Galatite | $2 \cdot 10^{14}$ |
| Ferro | $10 \cdot 10^{-8}$ | Mica | $9 \cdot 10^{13}$ |
| Mercurio | $95.78 \cdot 10^{-8}$ | Olio per trasformatori | $5 \cdot 10^{11}$ |
| Nichel | $7.8 \cdot 10^{-8}$ | Porcellana | $3 \cdot 10^{12}$ |
| Piombo | $22 \cdot 10^{-8}$ | Quarzo | $2 \cdot 10^{16}$ |
| Platino | $10 \cdot 10^{-8}$ | Vetro | $1 \cdot 10^{11}$ |
| Rame | $1.72 \cdot 10^{-8}$ | Zolfo | $1 \cdot 10^{15}$ |
Va notato che l’intensità di corrente, la differenza di potenziale e la resistenza di un materiale si possono misurare l’una indipendentemente dall’altra. La prima legge di Ohm prescrive che sussista tra queste grandezze una relazione ben precisa, ma le situazioni reali sembrano contraddire questa affermazione: la prima legge di Ohm, anche se applicata in regime stazionario, indica un limite ideale del comportamento di un conduttore, e rappresenta quindi un estremo verso cui le varie realizzazioni di una resistenza tendono. A titolo di esempio, possiamo rimandare all’effetto Joule: dipendendo la resistività di un materiale dalla sua temperatura, se, per effetto del passaggio di corrente elettrica il tratto di conduttore modifica la propria temperatura, cambierà anche la sua resistenza, facendo cadere così la prima legge di Ohm.