L'IS-LM è uno dei modelli più utilizzati nell'insegnamento della macroeconomia. Il modello venne sviluppato nel 1937 dall'economista britannico John Hicks come strumento per sintetizzare la teoria di John Maynard Keynes. Nonostante lo stesso Hicks, nel 1981, abbia criticato l'IS-LM per la sua scarsa attinenza ai dati macroeconomici, esso rimane uno dei migliori punti di partenza per l'insegnamento della disciplina.
Il suo punto di forza è la capacità di evidenziare relazioni macroeconomiche fondamentali, rimanendo allo stesso tempo semplice da comprendere.
È necessario tenere presente che questo modello si riferisce al breve periodo, cioè ad un periodo sufficientemente breve da non permettere variazioni significative della popolazione attiva e del livello dei prezzi. Per lo studio di queste variazioni è necessario fare riferimento a modelli di medio o lungo periodo, che non verranno affrontati in questa lezione.
Il modello, come facilmente intuibile dal nome, è composto da due curve: la curva IS e la curva LM.
La curva IS
La curva Investment-Saving (Investimento-Risparmio), in breve IS, rappresenta l'insieme dei punti nei quali il mercato dei beni è in equilibrio, ossia la produzione di beni è uguale alla domanda: possiamo scrivere l’equazione$$ (IS) \qquad Y = C + I (r) + G $$dove $Y$ rappresenta la produzione dell'economia, $C$ il consumo, $I$ l'investimento e $G$ la spesa del governo; $r$ è il tasso d’interesse. Una delle assunzioni su cui si basa questo modello, infatti, è che tutto il risparmio, pubblico e privato, sia investito: in altre parole, il risparmio è uguale all'investimento.
Rappresentiamo la curva IS in un piano, in cui poniamo in ascissa la produzione $Y$ e in ordinata il tasso $r$ d’interesse. Fondamentale per rappresentare la curva IS è chiarire la relazione fra investimento e produzione. L'investimento $I$ dipende in maniera inversamente proporzionale dal tasso di interesse $r$: maggiore è il costo di prendere in prestito il denaro, minore sarà l'investimento effettuato e quindi minore sarà la produzione. Difatti, $r$ rappresenta il costo del denaro.
Siccome lungo questa curva il mercato dei beni è in equilibrio, la sua equazione deve sempre essere soddisfatta.
Per fare un esempio, ad un aumento della spesa pubblica, $G' > G$, dovrà corrispondere un aumento della produzione, ovvero $Y' = C + I (r) + G' > Y$, e quindi uno spostamento della curva IS verso destra, come mostrato in figura:

Nel caso di produzione in eccesso, ossia $Y > C + I (r) + G$, il mercato dei beni non sarebbe in equilibrio, in quanto la produzione supererebbe la domanda.
Nella figura seguente, immaginiamo di essere in equilibrio sul mercato dei beni nel punto $E$:

Un aumento del tasso di interesse da $r$ a $r' > r$ farà sì che prendere denaro in prestito, ad esempio per finanziare un'iniziativa imprenditoriale, diventi più costoso: questo provocherà l'abbandono di alcuni di questi progetti, riducendo la produzione da $Y$ a $Y' < Y$ e riportando i mercati dei beni al nuovo punto di equilibrio $E'$, come illustrato nella figura.
La curva LM
Passiamo ora alla seconda metà del modello, la curva Liquidity-Money (ovvero Liquidità-Moneta), abbreviata in LM. Così come la curva IS rappresenta tutti i punti di equilibrio sul mercato dei beni, la curva LM rappresenta tutti i punti di equilibrio sul mercato finanziario, ovvero i punti in cui la domanda di moneta è uguale all'offerta di moneta:$$(LM) \qquad M = L (r, Y) $$dove $M$ rappresenta l'offerta di moneta e $L$ una funzione che descrive la domanda di liquidità, in funzione del tasso di interesse $r$ e della produzione $Y$.
L'idea alla base della curva LM è che la domanda di moneta sia direttamente proporzionale alla produzione (ad esempio, se si è più ricchi e si vuole fare più acquisti è necessario avere più contante per pagare). Il tasso d'interesse, come già detto in precedenza, rappresenta il costo della moneta.
L'offerta di moneta $M$ è mantenuta ad un certo livello dalla Banca Centrale. Dato che $M$ è costante, è facile derivare la curva LM: disegnandola nel piano già usato per la curva IS otteniamo un profilo come quello in figura.

Con riferimento alla figura precedente, immaginiamo di essere in equilibrio nel punto $E$. Un aumento della produzione da $Y$ a $Y’ > Y$ provocherà un aumento della domanda di moneta. Se l'offerta è costante e la domanda aumenta, il prezzo del denaro ovvero il tasso di interesse $r$ salirà a $r' > r$, riportando il mercato finanziario in equilibrio al punto $E'$: questo nuovo equilibrio sarà quindi caratterizzato da un tasso di interesse maggiore.
Analogamente a quanto detto per la curva IS, un aumento dell'offerta di moneta porterà la curva LM a spostarsi verso destra (viceversa, una riduzione dell'offerta di moneta sposterà la curva verso sinistra).
L'intersezione fra la curva IS e la curva LM rappresenta il punto di equilibrio dell'economia nel suo insieme, essendo in equilibrio sia i mercati dei beni che i mercati finanziari.
Il modello IS-LM ci permette di mostrare facilmente le conseguenze nel breve periodo di alcune politiche economiche.
Facciamo un esempio. Come mostrato precedentemente, un aumento della spesa pubblica, ovvero $G$, sposta la curva da IS a IS', più a destra:
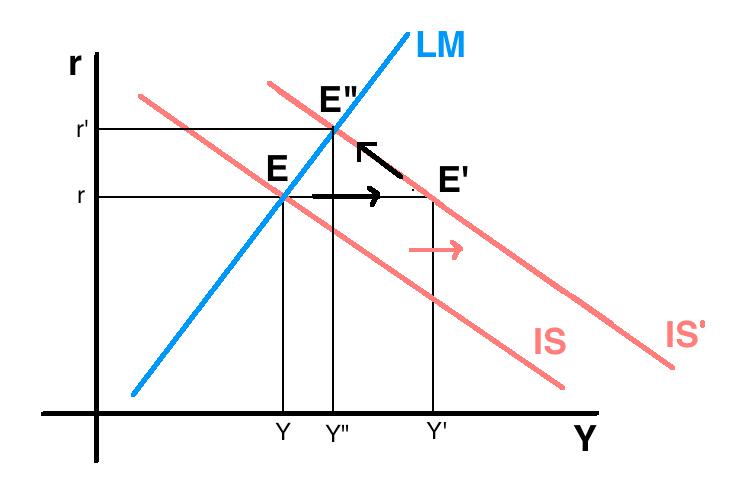
Nella figura, lo spostamento della curva IS muove l'equilibrio dal punto $E$ al punto $E'$.
Nel punto $E'$ il mercato dei beni è in equilibrio (ricorda: ogni punto della curva IS è equilibrio sul mercato dei beni!); il problema è che, non essendo $E'$ un punto della curva LM, il mercato finanziario non sarà in equilibrio. Quale sarà quindi la reazione dell'economia nel suo complesso?
L'aumento della produzione da $Y$ a $Y' > Y$, dovuto alla maggiore spesa pubblica, provocherà un aumento della domanda di moneta, il quale a sua volta si rifletterà in un aumento del tasso di interesse da $r$ a $r' > r$. Questo porterà alcuni investimenti ad essere abbandonati, riducendo parzialmente la produzione da $Y'$ a $Y'' < Y’$. L'economia raggiungerà quindi il punto $E''$ dove il mercato dei beni e il mercato finanziario sono in equilibrio. Questo equilibrio $E''$ sarà caratterizzato da una maggiore produzione e da un tasso di interesse maggiore rispetto all'equilibrio iniziale $E$.