In Geometria Euclidea si parla della retta come un ente primitivo: è cioè qualcosa che non si può definire utilizzando altri oggetti matematici, ma che può essere solo immaginato e “intuito” secondo il senso comune. Se lavoriamo nello spazio euclideo possiamo introdurre un altro ente primitivo: il piano. Possiamo pensare a un piano come all’equivalente di un foglio di carta perfettamente “piatto”, che però si estende indefinitamente in tutte le direzioni.
Nello spazio ci sono infinite rette e anche infiniti piani. Possiamo chiederci: che relazioni ci sono tra due piani nello spazio?
Definizione
Due piani nello spazio euclideo si dicono:
- incidenti se hanno un punto in comune;
- coincidenti se hanno tutti i punti in comune;
- paralleli se non hanno alcun punto in comune.
È possibile dimostrare (e anche intuire, a dire il vero) che se due piani sono incidenti hanno ben più di un punto in comune: anzi, hanno addirittura un’intera retta in comune, che passa proprio da quel punto.

Ciascuno di due piani incidenti viene diviso in due parti dalla retta che ha in comune con l’altro piano. Ciascuna di queste porzioni di piano viene detta semipiano, e la retta che la determina è detta origine del semipiano.
Come si può notare, le relazioni che ci sono tra due piani nello spazio sono esattamente le stesse relazioni che ci sono tra due rette nel piano; anche la terminologia è praticamente identica. Ma cosa succede invece a due rette nello spazio?
Definizione
Due rette nello spazio euclideo si dicono:
- incidenti se hanno un punto in comune;
- coincidenti se hanno tutti i punti in comune.
Se le rette invece non hanno punti in comune, distinguiamo due casi:
- se è possibile trovare un piano che contiene interamente entrambe le rette (cioè se le due rette sono complanari) allora le rette si dicono parallele;
- se invece tale piano non esiste, allora le due rette si dicono sghembe.
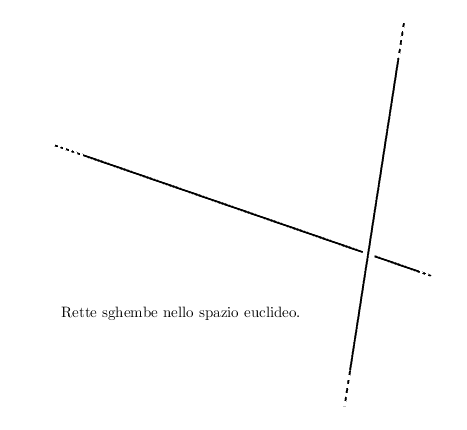
Vediamo dunque che nello spazio la situazione si complica rispetto a quanto accade nel piano: due rette che non hanno punti in comune possono essere sghembe, oltre che parallele. Intuitivamente, la ragione per cui questo accade è che quando ci sono tre dimensioni in gioco (anzichè due) le rette hanno una “direzione in più” grazie alla quale possono muoversi più liberamente nell’ambiente in cui sono definite.
È importante sottolineare inoltre che due rette incidenti sono necessariamente complanari. Questa affermazione trova fondamento analizzando alcuni postulati della Geometria euclidea, (come per esempio il fatto che per tre punti passa uno e un solo piano).
A questo punto rimane da capire quali sono le relazioni che ci possono essere tra una retta e un piano nello spazio.
Definizione
Una retta e un piano nello spazio euclideo si dicono:
- incidenti se hanno un solo punto in comune;
- paralleli se non hanno alcun punto in comune.
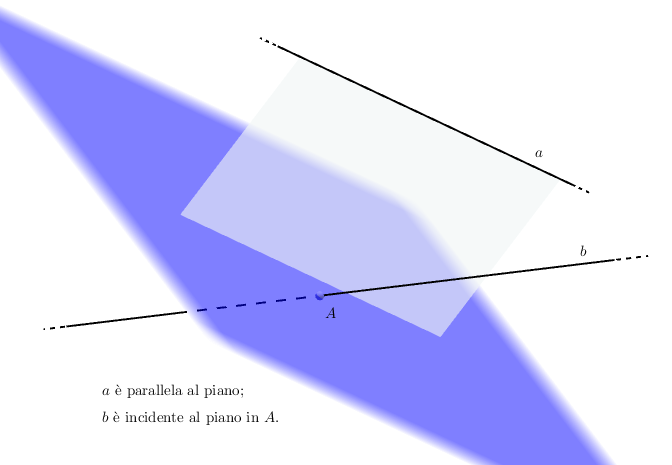
La definizione che abbiamo dato non è esaustiva, dato che una retta può anche essere interamente contenuta nel piano che stiamo considerando. In ogni caso non c’è una terminologia specifica per descrivere questa situazione.
Perpendicolarità nello spazio
Abbiamo visto poco fa che le relazioni tra due rette nello spazio sono un po’ più complesse rispetto a quelle che ci sono tra due rette nel piano. È legittimo quindi chiederci se la definizione di perpendicolarità tra rette nello spazio sia diversa rispetto a quella definita nel piano.
In realtà, la definizione è esattamente la stessa: due rette sono perpendicolari se sono incidenti, e se le quattro semirette che hanno origine il punto di incidenza formano quattro angoli retti. Da questo quindi deduciamo che:
- non ha senso parlare di perpendicolarità tra rette sghembe;
- due rette perpendicolari sono per forza incidenti, e quindi complanari.
È possibile definire il concetto di perpendicolarità tra retta e piano.
Definizione
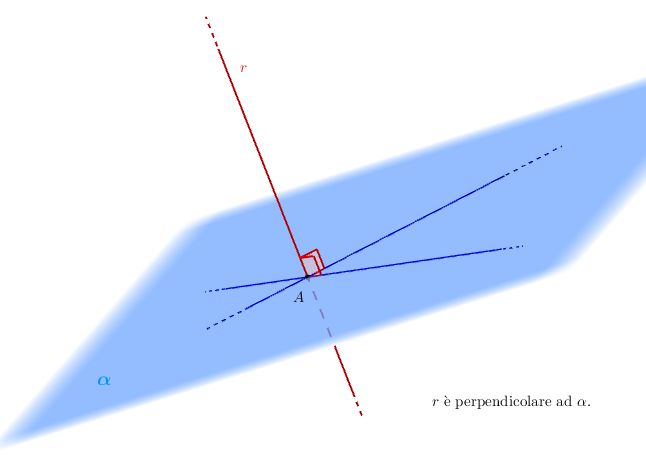
Una retta è perpendicolare a un piano se essa è incidente con il piano ed è perpendicolare a ciascuna retta contenuta nel piano stesso.
Chiaramente non possiamo pensare di poter verificare la perpendicolarità tra retta e piano controllando tutte le rette contenute nel piano, dato che esse sono infinite! Fortunatamente è possibile dimostrare - e quindi utilizzare - il seguente criterio di perpendicolarità:
Una retta è perpendicolare a un piano se e solo se è possibile individuare due rette del piano perpendicolari a essa.
Inoltre, una retta che è perpendicolare ad altre due rette distinte è perpendicolare al piano su cui giacciono queste due rette.
Enunciamo adesso un teorema molto importante della Geometria dello spazio, che non dimostriamo, che fa uso di molte delle definizioni che abbiamo appena mostrato.
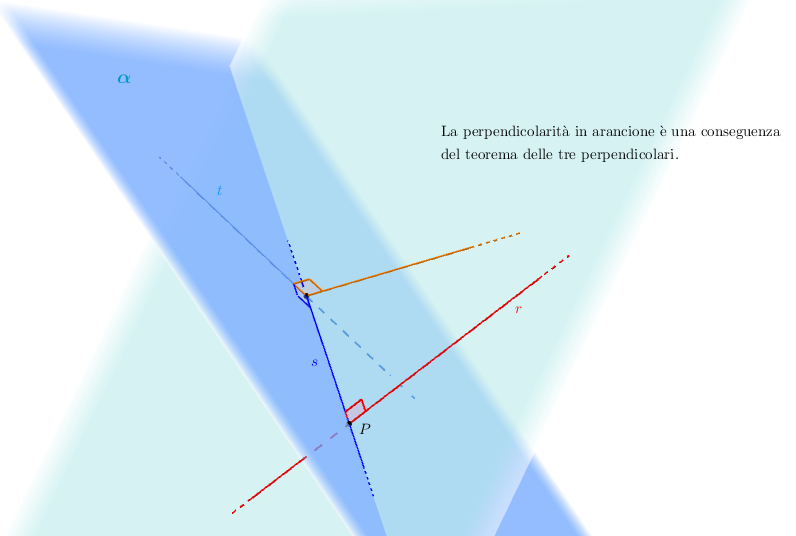
Teorema (delle tre perpendicolari): Consideriamo una retta $r$ perpendicolare a un piano $\alpha$ in un punto $P$ e conduciamo una qualsiasi retta $s$ contenuta in $\alpha$, passante per $P$; prendiamo anche una terza retta, che chiamiamo $t$, perpendicolare a $s$ e contenuta in $\alpha$. Allora $t$ è perpendicolare al piano su cui giacciono $r$ e $s$.
Definizione
Consideriamo due piani incidenti e i quattro semipiani che si vengono a creare. Una delle quattro regioni di spazio delimitate da due semipiani, compresi i semipiani stessi, è detta diedro o anche angolo diedro. L’origine dei semipiani è detta spigolo del diedro.
Due piani incidenti si dicono perpendicolari se si vengono a formare quattro diedri congruenti.

Il diedro è una sorta di estensione in tre dimensioni del concetto di angolo. Inoltre, in perfetta analogia con la definizione di angolo retto, ciascuno dei quattro diedri individuati da due piani perpendicolari è detto diedro retto. In effetti - come si vede in figura - ciascun piano perpendicolare allo spigolo di un diedro retto determina un angolo retto all’interno del diedro (i cui lati sono le semirette che si ottengono intersecando questo piano con i semipiani che delimitano il diedro).
È inoltre possibile mostrare che:
- se una retta è perpendicolare a un piano, qualsiasi piano contenente la retta è automaticamente perpendicolare al piano dato;
- se una retta è incidente ma non perpendicolare a un piano, esiste uno e un solo piano contenente la retta che sia anche perpendicolare al piano dato.