Uno degli enti primitivi della geometria euclidea è la retta. Siccome si tratta di un ente fondamentale, non proveremo a darne una definizione, ma una semplice descrizione. Una retta è innanzitutto una linea cioè un insieme di punti che, nella realtà, corrisponde a un tratto di matita disegnato su di un foglio con l’aiuto di una riga. Aggiungiamo inoltre che tale linea si estende senza limiti da una parte e dall’altra.
Spesso, sebbene in generale sia possibile considerarla come un oggetto dello spazio, la retta viene immaginata come un oggetto contenuto in un piano. La motivazione sta nel fatto che una linea retta, nella maggior parte dei casi, viene disegnata su un foglio: che è proprio il riferimento reale di quello che in geometria è stato idealizzato con il concetto di “piano” (anch’esso ente primitivo, così come “lo spazio”).

Notazione: una retta viene generalmente indicata con una lettera minuscola dell’alfabeto latino ($a, b, c \ldots$), un suo punto qualsiasi con una lettera maiuscola dell’alfabeto latino ($A, B, C \ldots$), mentre un piano viene indicato con una lettera minuscola dell’alfabeto greco ($\alpha, \beta, \gamma \ldots$).
Postulato: Si può stabilire una relazione d’ordine tra i punti di una retta, spesso chiamata verso della retta, in modo da dare un senso al concetto “il punto $A$ viene prima del punto $B$ sulla retta $r$”.

Definizione
Presa una retta dotata di un verso e un suo punto qualsiasi $O$, chiamiamo semiretta di origine $O$ l’insieme costituito dal punto $O$ stesso e dai punti di $r$ che precedono (o, in alternativa, che seguono) $O$ secondo il verso fornito.
Le due semirette generate naturalmente dalla scelta di un punto $O$ su di una retta vengono dette semirette opposte.

Relazioni tra rette: definizioni
Elenchiamo qui di seguito alcune delle principali definizioni riguardanti le rette, di fondamentale importanza per lo sviluppo della geometria euclidea.
Definizione
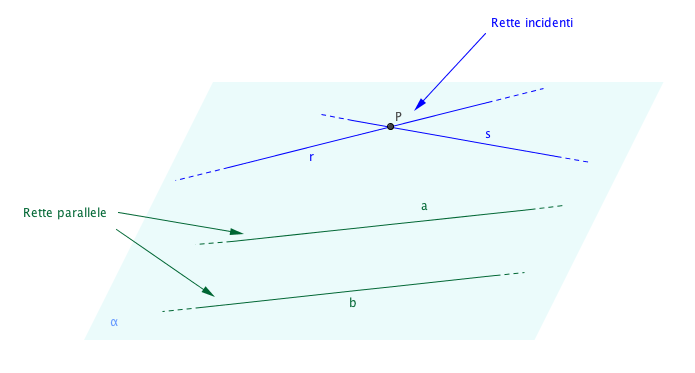
Consideriamo due rette $a$ e $b$ giacenti su un piano $\alpha$.
Se le rette non hanno alcun punto in comune, $a$ e $b$ si dicono parallele.
Se le rette hanno un punto in comune, $a$ e $b$ si dicono incidenti.
Come mai non consideriamo altri casi, come per esempio rette con due, tre o più punti in comune? La risposta sta nel seguente
Postulato: per due punti passa una e una sola retta.
Da questo segue che due rette che hanno più di un punto in comune sono coincidenti, cioè sono di fatto la stessa retta.
Definizione
L’insieme di tutte le rette di un piano che passano per un punto $C$ si dice fascio proprio di rette. $C$ viene detto centro del fascio.
L’insieme di tutte le rette di un piano parallele a una retta data (retta compresa) si dice fascio improprio.

Definizione
Due rette incidenti si dicono perpendicolari se le quattro semirette che hanno come origine il punto di incidenza sono lati di quattro angoli retti.

Definizione
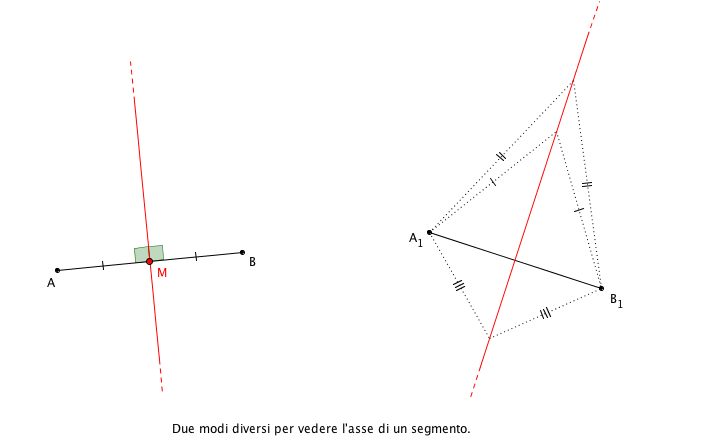
La retta perpendicolare a un segmento e giacente nel suo stesso piano, passante per il suo punto medio, viene detta asse del segmento. (N.B. la parola “asse” è maschile in questo contesto).
Alternativamente, l’asse di un segmento è l’insieme di tutti i punti equidistanti dagli estremi del segmento in questione e complanari a esso.