La circonferenza è un oggetto geometrico molto particolare: ci sono infatti molte sorprendenti proprietà che la caratterizzano. In questa lezione definiremo cosa sono gli angoli al centro e degli angoli alla circonferenza, e vedremo che relazione hanno con le corde e gli archi che essi sottendono.
Definizione
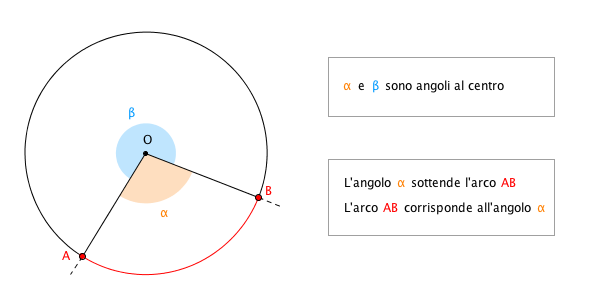
Un angolo al centro di una circonferenza è un angolo che ha il vertice nel centro della circonferenza considerata.
I lati dell’angolo intersecano la circonferenza in due punti $A$ e $B$; consideriamo l’arco $\overset{\frown}{AB}$ che ha tutti i punti compresi nell’angolo al centro. Diremo che questo arco corrisponde all’angolo al centro, e che l’angolo al centro sottende l’arco considerato.
Valgono le seguenti proprietà:
- la bisettrice di un angolo al centro divide a metà l’arco corrispondente;
- nella stessa circonferenza, due angoli al centro sono congruenti se e solo se gli archi corrispondenti sono congruenti; inoltre se un arco è maggiore di un altro arco, allora l’angolo che sottende il primo arco è maggiore dell’angolo che sottende il secondo (e viceversa).

Oltre a considerare angoli al centro e archi corrispondenti, possiamo considerare anche le corde sottese dagli archi in questione. Elenchiamo alcuni risultati utili che mostrano il legame tra questi oggetti geometrici.
- Una retta che passa per il centro di una circonferenza è perpendicolare a una corda se e solo se divide a metà la corda stessa, l’angolo al centro e l’arco corrispondente.

- L’asse di una corda di una circonferenza passa per il centro della circonferenza stessa.
- Nella stessa circonferenza, corde congruenti sono ugualmente distanti dal centro; inoltre se una corda è maggiore di un’altra corda, la distanza dal centro della prima corda sarà minore della distanza della seconda.

TEOREMA (delle corde): Se due corde di una circonferenza si intersecano, i segmenti che si formano su una di esse sono i medi e i segmenti sull’altra sono gli estremi di una stessa proporzione.

Angoli al centro e angoli alla circonferenza
Definizione
Un angolo alla circonferenza è un angolo convesso che ha vertice sulla circonferenza considerata, e tale per cui i suoi lati sono entrambi secanti la circonferenza, oppure uno secante e l’altro tangente.
Diremo che un angolo alla circonferenza insiste sull’arco che ha per estremi i punti di intersezione tra i lati dell’angolo e la circonferenza, ed è contenuto nell’angolo.
Dato un angolo alla circonferenza, si dice angolo al centro corrispondente l’angolo che ha il vertice nel centro della circonferenza e che sottende l’arco su cui insiste l’angolo alla circonferenza.

TEOREMA: un angolo alla circonferenza è la metà del suo angolo al centro corrispondente.

Da questo teorema discendono immediatamente due proprietà molto interessanti:
- ogni angolo che insiste su una semicirconferenza è retto (dato che il suo corrispondente angolo al centro è piatto);
- gli angoli alla circonferenza che insistono sullo stesso arco sono tutti congruenti: infatti, ciascuno di questi angoli ha il medesimo angolo al centro corrispondente, e pertanto sono tutti congruenti a metà dello stesso angolo.

Revisione scientifica a cura di Marco Guglielmino