Consideriamo due punti $A$ e $B$ nel piano cartesiano, di coordinate $(x_A, y_A)$ e $(x_B, y_B)$ rispettivamente. Se colleghiamo questi due punti otteniamo un segmento di estremi $A$ e $B$: su questo segmento possiamo determinare il suo punto medio $M$.
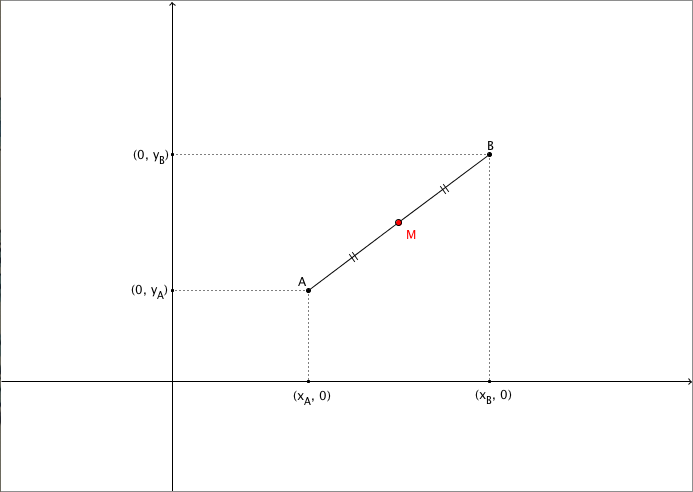
È possibile determinare le coordinate di $(x_M, y_M)$ di $M$ a partire dalle coordinate di $A$ e $B$, utilizzando il seguente risultato.
TEOREMA: Prendiamo due punti $A \equiv (x_A, y_A)$ e $B \equiv (x_B, y_B)$. L’ascissa $x_M$ e l’ordinata $y_M$ del punto medio $M$ del segmento di estremi $A$ e $B$ sono date dalle seguenti formule:$$x_M = \frac{x_A + x_B}{2} \qquad y_M = \frac{y_A + y_B}{2}$$Dimostrazione. Dividiamo l’analisi in due casi.
- Supponiamo che i punti $A$ e $B$ abbiano la stessa ordinata ($y_A = y_B$) e che $x_B > x_A$. In questo caso la formula per l’ordinata di $M$ è valida in automatico, dato che: $$y_M = y_A = \frac{y_A + y_A}{2} = \frac{y_A + y_B}{2}.$$Per determinare $x_M$, dobbiamo scoprire la lunghezza $\overline{AM}$, dato che $x_M = x_A + \overline{AM}$. Siccome $\overline{AB} = x_B - x_A$, allora per definizione di punto medio otteniamo: $$\overline{AM} = \frac{\overline{AB}}{2} = \frac{ x_B - x_A}{2}$$ e dunque: $$x_M = x_A + \frac{ x_B - x_A}{2} = \frac{2x_A + x_B - x_A}{2} = \frac{ x_A + x_B}{2}$$Abbiamo quindi dimostrato il teorema per due punti $A$, $B$ con ordinata uguale; un ragionamento analogo può essere fatto quando essi hanno la stessa ascissa.
- Supponiamo stavolta che $A$ e $B$ abbiano ascisse e ordinate differenti. Proiettiamo il segmento $AB$ su entrambi gli assi cartesiani: otteniamo due segmenti $CD$ e $EF$, con $C$ e $D$ appartenenti all’asse $x$ ed $E$, $F$ appartenenti all’asse $y$. Proiettiamo anche il punto $M$ su entrambi gli assi, ottenendo $M_1$ sull’asse $x$ e $M_2$ sull’asse $y$.
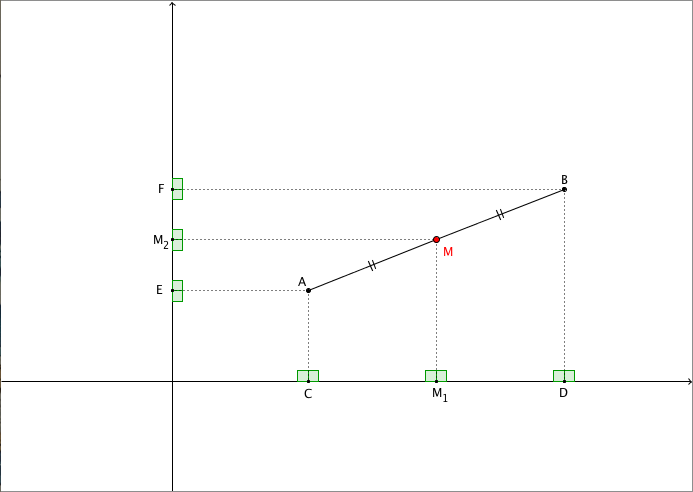
Dato che $CA$, $M_1M$ e $DB$ sono perpendicolari all’asse $x$ per costruzione, allora questi segmenti devono essere necessariamente paralleli fra loro. Ci troviamo quindi di fronte ad un fascio di rette parallele ($CA$, $M_1M$, $DB$) tagliato da due trasversali: l’asse $x$ e il segmento $AB$. Possiamo quindi applicare il teorema di Talete, ottenendo in particolare la relazione: $$CM_1 : M_1D = AM : MB$$A questo punto è sufficiente ricordare che $AM \cong MB$: questo significa allora che anche $CM_1 \cong M_1D$. Quindi $M_1$ è il punto medio di $CD$ e per quanto abbiamo visto al punto 1 la sua ascissa è data da: $$x_{M_1} = \frac{ x_C + x_D}{2}$$Per costruzione, abbiamo che:
##KATEX##\begin{aligned}x_{M_1} & = x_M \\x_C & = x_A \\x_D & = x_B\end{aligned}##KATEX## e quindi la nostra formula diventa: $$x_{M} = \frac{ x_A + x_B}{2}$$In questo modo abbiamo determinato l’ascissa del punto medio $M$.
Con un ragionamento del tutto analogo, osservando i segmenti $EA$, $M_2M$ e $FB$, è possibile mostrare che: $$y_M = \frac{ y_A + y_B}{2};$$quindi il teorema è dimostrato.
Vediamo qualche esercizio in cui possiamo applicare le formule che abbiamo appena determinato.
- Determinare il punto medio del segmento di estremi $A \equiv (3, 5)$ e $B \equiv (-1, -1)$.
Applichiamo direttamente le formule per trovare le coordinate di $M$:
##KATEX##\begin{aligned}x_M & = \frac{3 - 1}{2} = 1 \\y_M & = \frac{5 - 1}{2} = 2\end{aligned}##KATEX##
Quindi il punto medio di $AB$ ha coordinate $M \equiv (1, 2)$. - Dato il punto $A \equiv (-2, 3)$, trovare il punto $B$ tale per cui il segmento $AB$ abbia come punto medio $M \equiv (5, -2)$.
In questo caso dobbiamo applicare le formule del punto medio “all’inverso”:
##KATEX##\begin{aligned}x_M = \frac{x_A + x_B}{2} & \quad \Rightarrow & 5 = \frac{-2 + x_B}{2} & \quad \Rightarrow & x_B = 12; \\y_M = \frac{y_A + y_B}{2} & \quad \Rightarrow & -2 = \frac{3 + y_B}{2} & \quad \Rightarrow & y_B = -7.\end{aligned}##KATEX##
In conclusione il punto che cerchiamo ha coordinate $B \equiv (12, -7)$.