Consideriamo una retta e una circonferenza nel piano. Che rapporti possono avere tra di loro? In questa lezione daremo le definizioni di retta tangente e retta secante a una circonferenza, e enunceremo tre teoremi fondamentali (e molto utili per svolgere gli esercizi relativi a questo argomento).
Definizione
Consideriamo una retta $r$ e una circonferenza $C$ nel piano. Diremo che:
- $r$ è esterna a $C$ se $C \cap r = \emptyset$, cioè se la retta e la circonferenza non hanno punti in comune;
- $r$ è tangente a $C$ se $C \cap r = P$, cioè se la retta e la circonferenza hanno solo un punto in comune, che viene chiamato punto di tangenza;
- $r$ è secante di $C$ se $C \cap r = \{ P, Q \}$, cioè se la retta e la circonferenza hanno due punti in comune.

Lo studio delle rette tangenti a una circonferenza (e a una curva generica, in realtà) ha particolare rilevanza. Elenchiamo alcune proprietà delle rette tangenti a una circonferenza.
- Presa una tangente a una circonferenza, il raggio che ha come estremo il punto di tangenza è perpendicolare alla tangente considerata.
- Preso un punto esterno a una circonferenza $C$, esistono sempre due rette tangenti a $C$ che passano per il punto considerato. Se il punto è interno, da esso non passa alcuna tangente a $C$; se il punto appartiene alla circonferenza, invece, esiste un’unica tangente.

TEOREMA (delle tangenti): Consideriamo un punto $P$ esterno a una circonferenza $C$ di centro $O$, e da $P$ conduciamo le tangenti a $C$. Chiamiamo $A$ e $B$ i punti di tangenza. Allora:
- $PA \cong PB$;
- Il segmento $PO$ divide a metà l’angolo $\widehat{APB}$ e anche l’angolo $\widehat{AOB}$.

Dato che l’angolo $\widehat{APB}$ è diviso a metà da $PO$, abbiamo in automatico che la corda $AB$ è perpendicolare a $OP$ e anche che $AH \cong HB$.
TEOREMA (delle secanti): Consideriamo una circonferenza $C$ e due rette secanti $r$, $s$ che hanno in comune un punto $P$ esterno alla circonferenza. Detti $A$ e $B$ i punti di intersezione di $r$ e $C$ (con $PA < PB$), e detti $D$ e $E$ i punti di intersezione di $s$ con $C$ (con $PD < PE$) abbiamo la seguente proporzione: $PA : PD = PE : PB$.

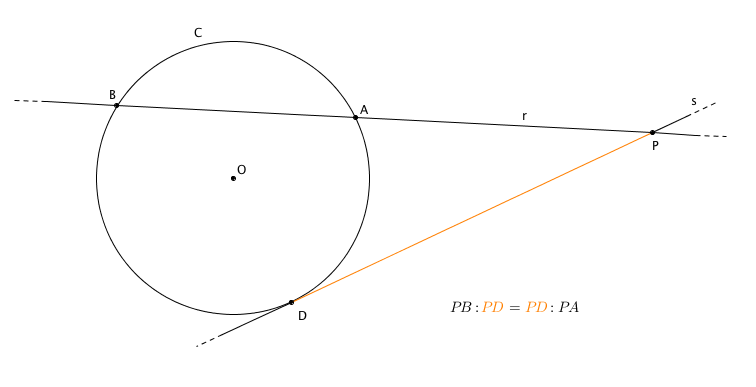
TEOREMA (della secante e della tangente): Consideriamo una circonferenza $C$, una retta secante $r$ e una retta tangente $s$ che hanno in comune un punto $P$ esterno alla circonferenza. Detti $A$ e $B$ i punti di intersezione di $r$ e $C$ (con $PA < PB$), e detto $D$ il punto di tangenza di $s$ rispetto a $C$, abbiamo la seguente proporzione: $PB : PD = PD : PA$.
Revisione scientifica a cura di Marco Guglielmino