La forza è quella grandezza fisica responsabile della modifica di uno stato di quiete o moto rettilineo uniforme, come per il principio di inerzia: si tratta di una grandezza vettoriale, applicata a un punto, in cui è concentrata una certa quantità di massa.
Ma che cosa succede se la massa non è concentrata in un solo punto, ma distribuita, con una certa densità, in un corpo esteso? In altre parole, come dobbiamo trattare il caso in cui la forza è applicata non a un punto, ma a qualcosa che possiede un’estensione?
Definizione
Supponiamo che una certa forza $\vec{F}$ venga applicata ad una superficie $\mathcal{S}$, e chiamiamo $S$ la misura dell’area di questa superficie. Allora la pressione $p$ esercitata dalla forza $\vec{F}$ sulla superficie $\mathcal{S}$ è il rapporto tra la forza in direzione normale alla superficie e l’area cui è applicata; in formule, $$ {p} = \frac{{F}_\perp}{S} $$ .

L’unità di misura della pressione, nel Sistema Internazionale, è ottenuta dall’unità di misura della forza (il newton $\text{N}$) e quella dell’area (il metro quadro $\text{m}^2$), ed è il pascal $\text{Pa}$: un pascal è la pressione che una forza di un newton esercita su una superficie di un metro quadrato, ossia $$1 \text{ Pa} = \frac{1 \text{ N}}{1 \text{ m}^2}$$ Ricordando che $1 \text{ N} = 1 \text{ kg m}\text{ s}^{-2}$, otteniamo $1 \text{ Pa} = 1 \text{ kg } \text{m}^{-1}\text{s}^{-2}$.
Storicamente, la pressione ha acquisito varie unità di misura. Esse sono, principalmente: il bar $\text{bar}$ e il suoi sottomultipli millibar $\text{mbar}$ e microbar $\mu\text{bar}$, l’atmosfera $\text{atm}$, e il millimetro di mercurio o torr $\text{mmHg} = \text{ torr}$.
Il bar, in simboli $\text{bar}$, è l’unità di misura della pressione nel sistema CGS (centimetro-grammo-secondo), ed equivale alla pressione esercitata dalla forza di un milione di dyne su un’area di un centimetro quadrato. Ricordiamo che il dyne è l'unità di misura della forza del sistema CGS, e vale $1 \text{ dyne} = 1\text{ g} \text{ cm} \text{ s}^{-2}$. Convertendo le unità di misura, si ottiene che $1 \text{ bar} = 10^5 \text{ Pa}$. In metereologia, è molto usato il millibar, $1 \text{ mbar} = 10^2 \text{ Pa}$; in acustica, si usa il microbar, $1 \mu\text{bar} = 10^{-1} \text{ Pa}$.
L’atmosfera è la pressione esercitata mediamente, al livello del mare, a $0^\circ$ di temperatura e a $45^\circ$ di latitudine, da una colonna d’aria alta quanto l’atmosfera terrestre su un’area di $ 1 \text{ cm}^2 $, cioè quella che comunemente si definisce pressione atmosferica. Empiricamente, vale $1 \text{ atm} = 101325 \text{ Pa} \equiv 1,01 \cdot 10^5 \text{ Pa}$. L’atmosfera si usa comunemente per misurare la pressione negli pneumatici o in altri dispositivi atti a contenere gas compressi.
Lo scienziato Evangelista Torricelli (1608 - 1647) introdusse l'unità di misura del torr, in simboli $\text{torr}$: mediante i suoi esperimenti, si arriva all’equivalenza $1 \text{ atm} = 760 \text{ torr}$, ossia $1 \text{ torr} = \frac{1}{760} \text{ atm}$. Vale inoltre l’equivalenza $1 \text{ torr} = 133,3 \text{ Pa}$.
Il millimetro di mercurio $\text{ mmHg}$ invece è la pressione esercitata dal peso di una colonna di mercurio alta $1 \text{ mm}$ su una base $1 \text{ cm}^2$, a $0^\circ$ di temperatura, al livello del mare e a $45^\circ$ di latitudine sulla superficie terrestre. È praticamente equivalente al $\text{ torr}$. Il millimetro di mercurio è usato per lo più in medicina.
A parità di forza, la pressione è inversamente proporzionale all’area cui è applicata: per esempio, se l’area a disposizione viene dimezzata, la pressione raddoppia. Al contrario, a parità di superficie disponibile, la pressione è direttamente proporzionale alla forza. Dalla definizione di pressione ricaviamo anche $ \vec{F}_{\perp} = \vec{p} S $.
Nella definizione di pressione, abbiamo introdotto la forza in direzione normale. Questo significa che abbiamo scomposto la forza, che può avere una direzione arbitraria, nelle sue componenti vettoriali nelle direzioni normale alla superficie e tangente alla superficie, di modo che $ \vec{F} = \vec{F}_\perp + \vec{F}_\parallel $: $\vec{F}_{\perp}$ è la componente normale della forza, $\vec{F}_{\parallel}$ è la componente della forza tangente alla superficie.
Se la direzione della forza è quella normale alla superficie, la forza coincide con la sua componente normale, e dunque la pressione esercitata sull’area $S$ è $ p = \frac{F}{S} $.

Se la direzione della forza non è quella normale alla superficie, consideriamo l’angolo $\vartheta$ che formano queste due direzioni: la componente normale della forza è data dalla proiezione del vettore $F$ sulla direzione perpendicolare, $F_{\perp} = F \cos(\vartheta)$, e dunque la pressione, più in generale, è $$ p = \frac{F \cos(\vartheta)}{S} $$
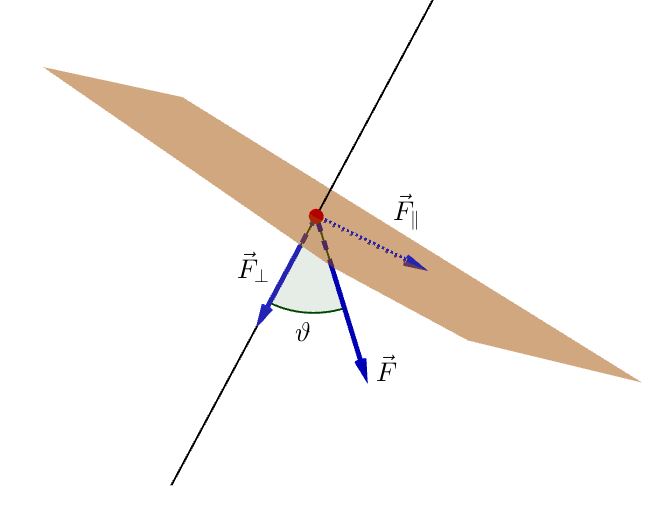
Si noti che la direzione normale alla superficie e la direzione della forza sono la stessa se $\vartheta = 0$, e siccome $\cos(0) = 1$ dalla formula appena esposta ricaviamo la precedente.