Ogni narrazione ha i suoi protagonisti che intraprendono azioni e interagiscono tra di loro all’interno di un scenario definito. Anche la scienza, come tutte le narrazioni, obbedisce a questo schema.
Ma se lo scenario che essa stessa si è scelta è il mondo materiale di cui noi esseri umani abbiamo esperienza, quali sono i suoi protagonisti?
Definizione
Una possibile risposta è quella di identificare questi ultimi con le grandezze fisiche: tutti quegli aspetti della realtà che possono essere misurati. Per identificare una grandezza è necessario fornirne una definizione operativa: bisogna, cioè, descrivere la procedura da seguire per ottenere una stima quantitativa, ovvero un numero, che descriva uno specifico aspetto di un particolare evento o oggetto. Una delle occupazioni principali degli scienziati è infatti scoprire e verificare leggi matematiche che mettano in relazione le misure di grandezze diverse.
Ridotta all’osso, una misura consiste nello stabilire un confronto tra il fenomeno che stiamo osservando e un qualche campione che faccia da riferimento: l’unità di misura.
Esempio
Per rendere un po’ più concreto il discorso facciamo un esempio: la lunghezza. Innanzitutto è necessario stabilire l’unità di misura. Nel nostro caso può essere una qualsiasi asticella rigida e diritta che, nel nostro esempio, chiameremo rod. A questo punto per misurare la lunghezza di un tavolo è sufficiente contare quante asticelle identiche lunghe un rod sarebbe necessario allineare, una in fila all’altra, per coprire il lato che vogliamo quantificare, partendo da uno spigolo per arrivare fino a quello opposto. Il numero che otteniamo è la lunghezza del tavolo in rod.
La scelta che abbiamo fatto nel nostro esempio in realtà non è molto felice: una buona unità di misura, per essere utile, deve essere la stessa per il maggior numero di persone ovvero quanto più possibile universale; in caso contrario il risultato non è lo stesso per tutti ed è facile che si creino fraintendimenti. Se parliamo di lunghezza ovviamente non c’è una sola unità di misura al mondo, tuttavia quella che ha la più ampia diffusione internazionale è il metro.
Detto questo c’è ancora un aspetto da tenere presente. Scelta una qualsiasi unità di misura (come per esempio il metro) saranno davvero pochissime le volte in cui la lunghezza di un oggetto corrisponderà esattamente a un numero intero di metri. Per questo motivo si ricorre ai sottomultipli dell’unità in modo da fornire un’approssimazione sempre migliore della grandezza misurata.
Ciononostante è impossibile raggiungere una precisione assoluta: tutte le misure sono caratterizzate da una specifica incertezza che deve essere a sua volta quantificata per poter stabilire l’affidabilità della misura.
L’incertezza dipende soprattutto dallo strumento che viene usato per effettuare la misura. In particolare è legata alla sensibilità dello strumento stesso, ovvero la più piccola quantità della grandezza considerata che lo strumento stesso riesce a misurare.
Definizione
Le grandezze fisiche hanno caratteri differenti, i quali ci permettono di distinguerle e classificarle in grandezze fondamentali e grandezze derivate.
Le grandezze fondamentali sono quelle per le quali l’unità di misura è scelta indipendentemente da altre unità, ed è possibile definire questa unità il più universalmente possibile, di modo che il maggior numero di persone possano concordare sulla sua misura.
Per riprendere il nostro esempio, inizialmente, nel 1791, il metro venne definito come la decimilionesima parte del meridiano che corre tra il polo Nord e l’equatore terrestre. Questo ovviamente pone il problema di mettersi tutti d’accordo su quanto misuri effettivamente quel meridiano. Nel corso del tempo la definizione cambiò, per raggiungere i criteri di universalità ed invarianza appena definiti: si passò dalla lunghezza del meridiano alla distanza tra due tacche incise su una barra di una lega di platino e iridio, a $1650763,73$ lunghezze d’onda di una radiazione emessa nel vuoto da un atomo di kripton-86 quanto passa da un livello energetico $2 p^{10}$ a $5 d^5$, sino ad arrivare alla definizione attuale, adottata nel 1983, la $299792458$-esima parte della distanza percorsa dalla luce nel vuoto in un secondo. Come si può vedere, definire l’unità di misura di una grandezza fondamentale non è affatto facile.
Le grandezze derivate sono invece quelle grandezze definite attraverso quelle fondamentali tramite operazioni matematiche.
Per esempio, l’unità di misura della velocità è definita come rapporto tra spazio e tempo, e dunque è, nel Sistema Internazionale, $m \ / \ s$; l’area si può misurare moltiplicando una lunghezza (base) per un’altra lunghezza (altezza), quindi la sua unità di misura è $m \ \cdot m = m^2$, il metro quadrato.
Definizione
Un’ulteriore distinzione stabilisce quali grandezze siano scalari e quali vettoriali.
Definiamo una grandezza scalare una grandezza fisica per la quale è sufficiente un’unica misura, ossia un solo numero ed un’unità di misura, per identificarla univocamente. La lunghezza, il tempo, la massa, la temperatura sono tutti esempi di grandezze scalari.
Ci sono invece altre grandezze la cui misura non è sufficiente ad identificarle del tutto: possedendo un numero ed un’unità di misura è possibile determinarne un solo aspetto. Per esempio, supponiamo di spostarci in avanti di $100$ metri, e, successivamente, di svoltare a destra e di proseguire per altri $100$ metri. Di quanto ci siamo spostati dal punto di partenza? Se lo spostamento fosse una grandezza scalare, l’algebra ci farebbe convenire che ci siamo spostati di $100 + 100$ $= 200$ metri. Ma un semplice ragionamento geometrico (e il teorema di Pitagora) ci fanno pervenire alla risposta corretta: ci siamo spostati di $\sqrt{2} \cdot 100$ metri.
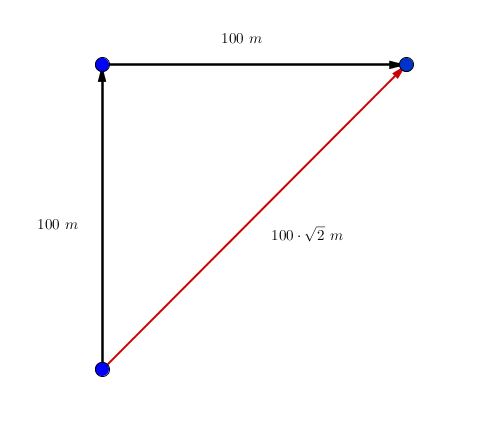
In che cosa differisce lo spostamento da una semplice lunghezza? Per identificare uno spostamento è anche necessario specificare, oltre di quanto ci si sposta, la direzione lungo la quale ci si sposta e il verso seguito lungo quella direzione. Più precisamente, una grandezza vettoriale è una grandezza fisica identificata non solo da una misura (cioè da un’unità di misura e da un numero), detta modulo, ma anche da una direzione, una retta, e un verso lungo tale direzione.
In questo corso ci occuperemo di misure, tralasciando altri aspetti delle grandezze fisiche. Per trattare tutti gli aspetti delle grandezze vettoriali, si faccia riferimento a questo corso.