Nonostante possa sembrare una questione banale o un inutile esercizio retorico, definire cosa sia effettivamente un insieme è un grosso problema, se affrontato con leggerezza. Verso la fine del XIX secolo, mossi dalla necessità di gettare delle solide basi per la matematica moderna (in alcuni campi, già ampiamente sviluppata), molti matematici tra cui Georg Cantor e Richard Dedekind fecero uno dei primi tentativi di costituire ciò che oggi potremmo chiamare i fondamenti della matematica, arrivando a una prima formulazione della Teoria degli Insiemi. Questa teoria è attualmente considerata di capitale importanza per la comprensione di quasi ogni ambito della matematica: per questo motivo, l’insegnamento di questo argomento inizia molto presto nelle scuole di oggi.
Definizione
In matematica, la parola insieme viene utilizzata per indicare un raggruppamento, una raccolta, una collezione di elementi distinti fra loro che rispettano inequivocabilmente una o più proprietà che definiscono l’insieme considerato.
Come appena visto, un insieme non può essere definito a partire da concetti più semplici; abbiamo utilizzato dei termini che nella lingua italiana sono sostanzialmente dei sinonimi, come “raggruppamento”, “collezione” e “raccolta”. Per questo motivo diremo che l’insieme è un ente primitivo, così come lo è una retta o un piano in Geometria Euclidea.
Un concetto primitivo è anche l’idea di appartenenza, ovvero la caratteristica di un certo elemento di essere contenuto (o non essere contenuto, in caso di non appartenenza) all’interno di un insieme.
Notazione: generalmente un insieme viene indicato con una lettera latina maiuscola ($A, B, C \ldots$ ma anche $X, Y, \ldots$) mentre un generico elemento di un insieme viene indicato con una lettera latina minuscola ($a, b, c, \ldots, x, y \ldots$).
Inoltre, quando un elemento $a$ appartiene a un insieme $A$, si scrive $a \in A$. Quando invece un elemento $a$ non appartiene ad $A$, si scrive $a \not \in A$.
Definizione
Diremo che un insieme è finito se è possibile contare i suoi elementi e il conteggio dei suoi elementi ha un termine. Il numero ottenuto alla fine del conteggio è detto cardinalità dell’insieme, e viene indicato con $\# A$.
Un insieme è invece detto infinito se non è finito.
Esiste un concetto di cardinalità anche per gli insiemi infiniti che è di fatto in grado di distinguere certe tipologie di insiemi, nonostante a un primo sguardo sembri che la cardinalità di un insieme infinito sia semplicemente “infinito”, dato che non si possono contare i suoi elementi. Il discorso è tuttavia molto delicato, e lo affronteremo in parte quando analizzeremo i numeri naturali.
Rappresentazioni di un insieme
Consideriamo l’insieme $A$ costituito dalle vocali della parola “insieme”. In quanti modi possiamo descrivere, o rappresentare questo insieme?
- un modo l’abbiamo implicitamente già trovato, appena abbiamo nominato $A$, descrivendo la proprietà che un oggetto deve possedere per appartenere ad $A$. In questo caso si parla di rappresentazione intensiva dell’insieme $A$, e in maniera rigorosa si scrive
$$A = \{ x \ | \ x \text{ è una vocale della parola “insieme”} \}$$ - un secondo modo, sicuramente più diretto, consiste nell’elencazione di tutti gli elementi contenuti in $A$, che nel nostro caso sono le lettere “i” ed “e”. In simboli, si scrive
$$A = \{i, e \}$$
ed è la rappresentazione estensiva di $A$. - il terzo modo, per certi versi simile alla rappresentazione estensiva ma molto più flessibile, è l’utilizzo dei diagrammi di Eulero-Venn. Si tratta di una rappresentazione grafica, dove l’insieme viene raffigurato come una regione chiusa del piano e ogni elemento appartenente all’insieme come un punto interno di questa regione. Nel nostro caso:
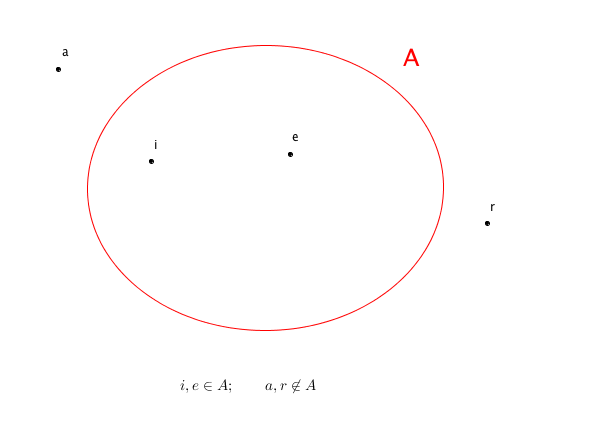
Quali sono gli svantaggi e i vantaggi di ciascuna di queste rappresentazioni?
- Rappresentazione intensiva
PRO: molto sintetica, precisa; fa capire al volo l’idea con cui è stato definito l’insieme.
CONTRO: si perdono di vista gli elementi veri e propri dell’insieme. - Rappresentazione estensiva
PRO: non c’è possibilità di sbagliarsi sugli elementi contenuti nell’insieme, permette un miglior controllo della situazione.
CONTRO: non è possibile rappresentare in maniera precisa insiemi infiniti. - Diagrammi di Eulero-Venn
PRO: di grande impatto visivo, permette di visualizzare facilmente le operazioni di intersezione, unione e complementare.
CONTRO: poco utilizzabile in caso di insiemi infiniti e quando si ha a che fare con numerosi insiemi.
Simbologia di base e prime definizioni
Definizione
Un insieme $A$ si dice vuoto quando non contiene alcun elemento, e scriviamo $A = \emptyset$.
Definizione
Diremo che due insiemi $A$ e $B$ sono uguali quando essi contengono esattamente gli stessi elementi.
Definizione
Quando ciascun elemento di un insieme $A$ è contenuto in un altro insieme $B$, diremo che $A$ è un sottoinsieme di $B$, e scriveremo $A \subseteq B$.
Notiamo che:
- nella definizione precedente non facciamo riferimento a eventuali altri elementi di $B$ che non siano anche in $A$, quindi potenzialmente $A$ e $B$ potrebbero essere uguali;
- l’insieme vuoto $\emptyset$ è automaticamente un sottoinsieme di qualsiasi altro insieme $B$. Infatti siccome l’insieme vuoto non contiene nessun elemento, la proprietà “gli elementi di $\emptyset$ sono contenuti in $B$” viene automaticamente verificata, perché non c’è alcun elemento di $\emptyset$ che non la soddisfa!
Per risolvere queste ambiguità, diremo che $A$ è un sottoinsieme proprio di $B$ se non è vuoto e se ci sono altri elementi di $B$ non contenuti in $A$.
Definizione
Prendiamo un insieme $A$. L’insieme costituito da tutti i sottoinsiemi di $A$ è detto insieme delle parti di $A$, e si indica con $\mathcal{P}(A)$.
È possibile dimostrare che, se $A$ è un insieme con $\# A = n$, allora $\# \mathcal{P}(A) = 2^n$.
La nozione di insieme delle parti non è semplice da fare propria: chiariamola con un esempio. Prendiamo l’insieme $A = \{x, y, z \}$ (che ha cardinalità $3$). Quali sono i sottoinsiemi di $A$? Elenchiamoli qui di seguito:
$$ A, \emptyset, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\}. $$
Notiamo che tra i sottoinsiemi di $A$ ci sono anche i sottoinsiemi “banali”, chiamati spesso singoletti, costituiti da un solo elemento. Essi NON sono da confondere con gli elementi stessi che contengono: sono infatti insiemi, non elementi!
L’insieme delle parti è l’insieme che contiene ogni sottoinsieme di $A$. Possiamo rappresentarlo estensivamente:
$$ \mathcal{P}(A) = \{ A, \emptyset, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\} \} $$
Effettivamente, la cardinalità di $\mathcal{P}(A)$ è $2^3 = 8$.
Revisione scientifica a cura di Marco Guglielmino.