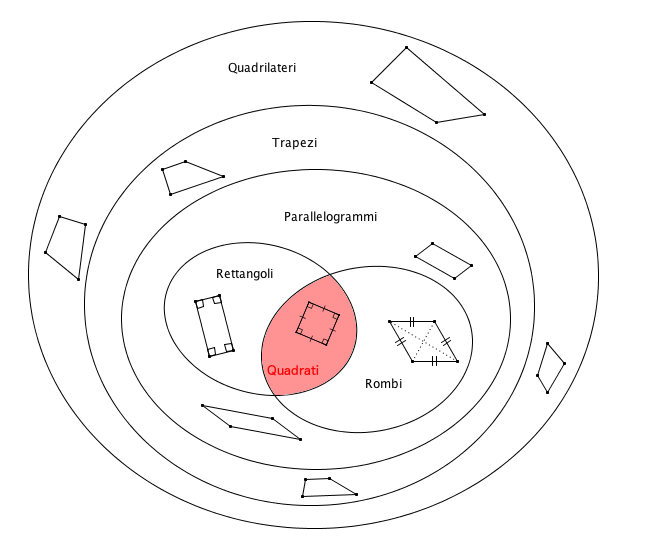
Il poligono regolare con quattro lati è detto quadrato. Essendo un poligono regolare, esso eredita tutte le proprietà di questi speciali poligoni; inoltre, assume un particolare ruolo in quanto “punto di arrivo” della classificazione dei quadrilateri, secondo la trattazione consueta.
Definizione
Un parallelogramma che abbia tutti gli angoli interni congruenti e tutti i lati congruenti è detto quadrato.
Per quanto detto nella definizione, quindi, un quadrato è contemporaneamente un rettangolo e un rombo. Inoltre, essendo equiangolo (cioè, con tutti gli angoli congruenti) ed equilatero (cioè, con tutti i lati uguali), è un poligono regolare.
Ciascun angolo interno del quadrato misura $\frac{\pi}{2}$ radianti, cioè $90^\circ$.
Come conseguenza delle proprietà che il quadrato eredita essendo un rombo e un rettangolo, abbiamo il seguente risultato.
TEOREMA (Caratterizzazione del quadrato): Un parallelogramma è un quadrato se e solo se le sue diagonali sono congruenti e perpendicolari tra loro, oppure se le diagonali sono congruenti e sono anche bisettrici degli angoli interni.
Formule del quadrato
Ogni quadrato è determinato univocamente a partire dalla misura del suo lato $l$, o dalla misura della sua diagonale $d$. Infatti:
Area: $A = l^2 = \frac{1}{2}d^2$
Perimetro: $2p = 4l = 2\sqrt{2}d$
Lato: $l = \sqrt{A} = \frac{2p}{4} = \frac{\sqrt{2}}{2}d$
Diagonale: $d = \sqrt{2A} = \frac{\sqrt{2}}{4}2p = \sqrt{2}l$
Dal punto di vista della classificazione dei quadrilateri, il quadrato si colloca nell’intersezione di tutti gli insiemi in cui i quadrilateri vengono suddivisi: