Dati due insiemi numerici $X$ e $Y$, si chiama funzione una relazione che associa, a ogni elemento $x$ di $X$ un unico elemento $y=f(x)$ in $Y$.
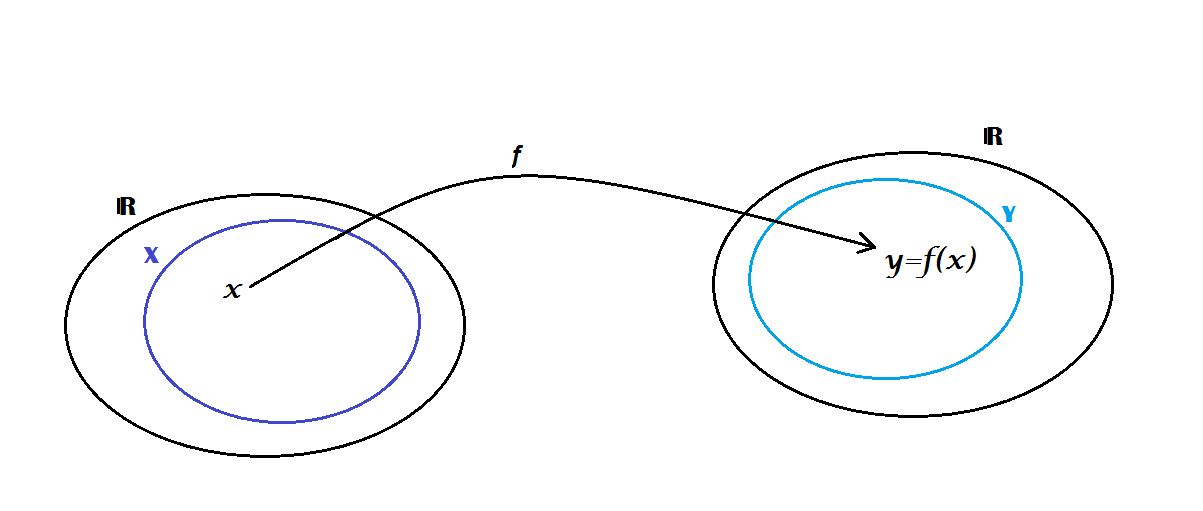
Il numero $y$ si chiama immagine di $x$ tramite la funzione $f$.
L’insieme $X$, detto dominio, è un sottoinsieme di $\mathbb{R}$ per cui ha senso la legge di definizione $f$. Esso contiene dei valori $x$ a cui può essere applicata la funzione $f$. Il dominio più grande possibile per una funzione viene detto dominio naturale o insieme di definizione.
L’insieme $Y$, detto codominio, è l’insieme di tutte le immagini della funzione $f$ a partire da $X$. Anche $Y$ è, in generale, un sottoinsieme di $\mathbb{R}$.
Quando si vuole determinare il dominio più grande di una funzione bisogna controllare i seguenti oggetti matematici:
- denominatori, che devono essere sempre posti diversi da zero;
- radici di indice pari, il cui radicando deve essere posto positivo o nullo;
- logaritmi, il cui argomento deve essere positivo;
- espressioni del tipo $[f(x)]^{g(x)}$, per cui si deve porre $f(x)>0$;
- funzioni trigonometriche inverse, il cui argomento deve essere compreso tra $-1$ e $1$.
In collaborazione con Elia Bombardelli, autore del canale youtube LessThan3math