Consideriamo una relazione tra due insiemi. Essa può essere visualizzata utilizzando la rappresentazione sagittale: ciascuna coppia di elementi in relazione viene collegata con una freccia, indicando che -come spesso si dice- il primo elemento viene “mandato” nel secondo.
Consideriamo la relazione $\mathscr{R}$ mostrata in figura:

Possiamo notare che l’elemento $a \in A$ è associato a due elementi distinti $m,n \in B$; ovvero, da $a$ partono due frecce dirette verso $m$ e $n$. Abbiamo quindi una ambiguità: dove verrà mandato $a$ da $\mathscr{R}$? Come facciamo a scegliere un arrivo “privilegiato” se partiamo da $a$?
Questa situazione, in molti casi, non è considerata accettabile. Per questo motivo verrà introdotto un particolare tipo di relazione, costruita in modo tale per cui la situazione appena mostrata non accada mai.
Definizione
Consideriamo una relazione $f$ con dominio $D \subseteq A$ e codominio $C \subseteq B$. Diremo che $f$ è una funzione se ogni elemento del suo dominio è associato a uno e un solo elemento del suo codominio.
Se $xfy$ diremo anche che $y$ è immagine di $x$ e che $x$ è controimmagine di $y$.
Notazione: generalmente, una funzione tra $A$ e $B$ viene indicata con una lettera latina minuscola, come per esempio $f$, e si scrive $f : A \rightarrow B$ per riassumere il tutto. Se $D$ è il dominio di $f$, allora si scrive anche $f: D \subseteq A \rightarrow B$ e il codominio $C$ di $f$ viene indicato a volte con $f(A)$ o $f(D)$.
Quando $xfy$, cioè $(x, y) \in f$, si usa scrivere $f(x) = y$ , o $y = f(x)$, o anche $f: x \mapsto y$.
Che cosa differenzia una funzione da una generica relazione, dal punto di vista della rappresentazione sagittale e cartesiana?
- Nella rappresentazione sagittale di una funzione non esiste alcun elemento dell’insieme di partenza con più di una freccia che parte da esso (e qua ci colleghiamo al discorso che abbiamo fatto all’inizio della lezione):

- Nella rappresentazione cartesiana di una funzione non esiste più di una coppia $(x, y)$ con $f(x) = y$ che sta sulla stessa retta verticale:

Definizione
Una funzione $f: A \rightarrow B$ si dice iniettiva se ogni elemento di $B$ è associato al massimo a un solo elemento di $A$. In simboli, $$f \text{ è iniettiva} \quad \Leftrightarrow \quad f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \quad \forall x_1, x_2 \in D \subseteq A$$o anche $$f \text{ è iniettiva} \quad \Leftrightarrow \quad x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2) \quad \forall x_1, x_2 \in D \subseteq A.$$
Definizione
Una funzione $f: A \rightarrow B$ si dice suriettiva se $C = B$, ovvero se ogni elemento di $B$ è associato ad almeno un elemento di $A$. In simboli, $$f \text{ è suriettiva} \quad \Leftrightarrow \quad \forall b \in B, \exists a \in A \text{ tale che } f(a) = b.$$
Definizione
Una funzione si dice biettiva, o biunivoca, se è sia iniettiva che suriettiva.
Come possiamo capire se una funzione è iniettiva o suriettiva a partire dalla sua rappresentazione?
- Nella rappresentazione sagittale, se $f$ è una funzione iniettiva, significa che ogni elemento $b \in B$ è toccato al massimo da una freccia, perchè altrimenti vorrebbe dire che più di un elemento di $A$ è associato a $b$ (sottolineiamo che se nessuna freccia tocca $b$, questo non impedisce a $f$ di essere iniettiva).
Una funzione è suriettiva se ciascun elemento di $B$ viene raggiunto da almeno una freccia.
- Nella rappresentazione cartesiana, una funzione è iniettiva se non esiste più di una coppia $(x, y)$ con $f(x)=y$ che sta sulla stessa retta orizzontale.
Una funzione è suriettiva se in ogni retta orizzontale è presente almeno una coppia $(x,y)$ con $f(x) = y$.
ATTENZIONE: una funzione può tranquillamente non essere né iniettiva né suriettiva; alla fine della lezione ne vedremo un esempio (quando analizzeremo le funzioni reali a variabile reale).
Consideriamo ora una generica funzione $f: A \rightarrow B$ visualizzata secondo la rappresentazione sagittale, e supponiamo di invertire il verso di ciascuna freccia. Cosa otteniamo? Sicuramente otteniamo una relazione $g$ da $B$ ad $A$, cioè un sottoinsieme del prodotto cartesiano $B \times A$ (abbiamo semplicemente scambiato l’ordine delle coppie appartenenti ad $f$) ma non possiamo essere certi, a priori, che questa relazione sia di nuovo una funzione.
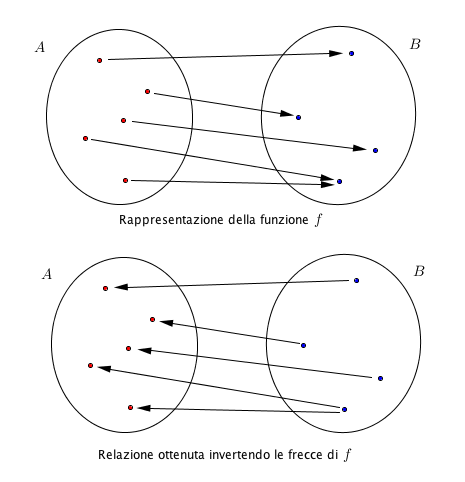
Ci si accorge che il problema si presenta quando più di una freccia di $f$ punta verso uno stesso elemento $b$, ovvero quando $f$ non è iniettiva. Infatti, una volta invertito il verso di quelle frecce, il risultato sarà una relazione $g$ tale per cui da $b$ parte più di una freccia, che è esattamente quello che non deve verificarsi affinché $g$ sia una funzione.
Definizione
Una funzione $f: A \rightarrow B$ si dice invertibile se la relazione ottenuta invertendo le coppie di elementi in relazione secondo $f$ è ancora una funzione. Tale funzione viene indicata con $f^{-1}: B \rightarrow A$ e viene chiamata funzione inversa di $f$.
La funzione inversa $f^{-1}$, se esiste, fa esattamente quello che fa $f$, ma al contrario; se $f(x) = y$, allora $x = f^{-1}(y)$.
Per quanto detto prima, se una funzione non è iniettiva di certo non è invertibile. Inoltre, presa una funzione iniettiva $f$, è sempre possibile trovare la sua inversa $f^{-1}$, a patto di considerare opportuni dominio e codominio (non sempre il dominio di $f^{-1}$ coincide con $B$, per esempio).
Definizione
Una funzione $f$ si dice costante se ogni elemento del dominio ha la stessa immagine.
Definizione
Due funzioni $f$ e $g$ si dicono uguali quando hanno lo stesso dominio $D$ e quando $f(a) = g(a)$ per ogni scelta di $a \in D$.
Esempi notevoli: le funzioni $f: \mathbb{R} \rightarrow \mathbb{R}$
Molto spesso, quando in Matematica si parla di “funzioni”, in realtà si parla di una funzione del tipo $f \mathbb{R} \rightarrow \mathbb{R}$, ovvero si sceglie $A = B = \mathbb{R}$. Le funzioni reali di variabile reale (è così che vengono chiamate questo tipo di funzioni) sono concetti fondamentali all’interno dell’Analisi Matematica; quando si parla di uno studio di funzione, infatti, si sta molto spesso considerando proprio questo speciale tipo di funzione.
Dato che i numeri reali costituiscono un insieme infinito non numerabile, la rappresentazione sagittale è una scelta infelice per una funzione di questo tipo: potenzialmente, dovremmo disegnare un numero infinito non numerabile di frecce! La rappresentazione cartesiana è, invece, molto adatta a questa situazione: infatti $\mathbb{R}$ viene solitamente rappresentato come una retta orientata, e il prodotto cartesiano $\mathbb{R} \times \mathbb{R}$ diventa in maniera naturale un piano - il piano cartesiano - dotato di un sistema di riferimento, che altro non è che l’unione delle due rette che rappresentano $A = \mathbb{R}$ e $B = \mathbb{R}$.

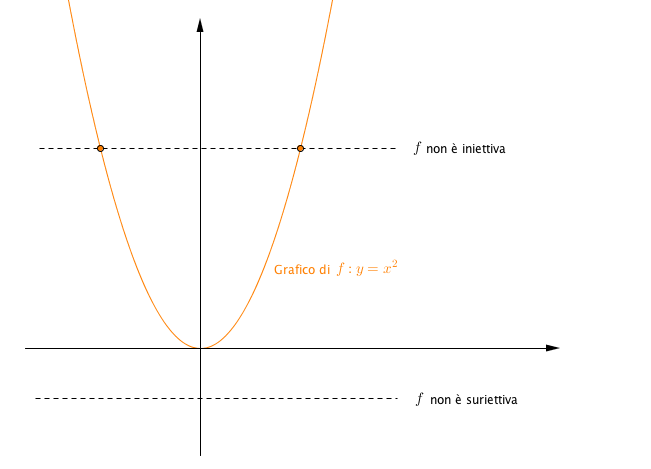
Come esempio, consideriamo la funzione$f: \mathbb{R} \rightarrow \mathbb{R}$ che consiste nell’elevamento al quadrato, così definita: $$y = f(x) \quad \Leftrightarrow \quad y = x^2, \quad x \in A=\mathbb{R}, y \in B=\mathbb{R}.$$ Questa funzione manda ciascun $x$ nel suo quadrato $y = x^2$.
- $f$ non è iniettiva: infatti esistono degli $y \in B = \mathbb{R}$ che sono in relazione con più di un elemento $x \in A = \mathbb{R}$. Per esempio, $y = 9$ è in relazione sia con $3$ che con $-3$, dato che $9 = (-3)^2 = 3^2 $.
- $f$ non è suriettiva: infatti esistono degli $y \in B = \mathbb{R}$ che non sono in relazione con nessun $x \in A = \mathbb{R}$. Per esempio, $y = -4$ non è il quadrato di nessun numero reale.
- Dato che $f$ non è iniettiva, non è neanche biettiva, e non è nemmeno invertibile.
Notiamo però che, a patto di restringere il dominio di $f$ da $\mathbb{R}$ a $\mathbb{R}^+ \cup \{ 0\}$ (cioè limitando il calcolo di $f$ ai numeri reali positivi e allo zero) allora la funzione diventa a tutti gli effetti invertibile, perché in $\mathbb{R}^+ \cup \{ 0\}$ la funzione è certamente iniettiva. Questa situazione è molto comune nell'analisi delle funzioni reali di variabile reale, e permette in alcuni casi di ricavare una funzione invertibile a partire da un "pezzo" di una funzione che non lo è.
Vediamo che nella rappresentazione cartesiana di $f$ le coppie in relazione fra loro formano una linea continua, che viene solitamente chiamata grafico di $f$.
Revisione scientifica a cura di Marco Guglielmino