All’interno delle sezioni coniche (dette anche coniche, semplicemente) troviamo una particolare tipologia di curva: l’ellisse. Quando siamo nell’ambito della Geometria Analitica, di solito, si studiano ellissi che abbiano assi paralleli agli assi cartesiani: questa scelta viene fatta per semplificare le equazioni che definiscono l’ellisse stessa.
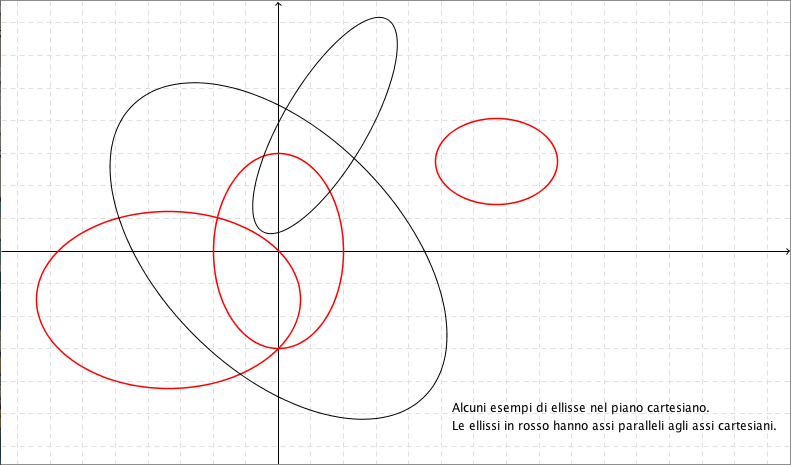
In realtà possiamo definire l’ellisse anche come un particolare luogo geometrico.
Definizione
Dati due punti del piano $F_1$ e $F_2$, detti fuochi, definiamo ellisse l’insieme dei punti del piano tali per cui la somma della distanza tra ciascuno di essi e i fuochi sia costante.
Consideriamo la retta che congiunge i fuochi $F_1$ e $F_2$ di un’ellisse. Se questa retta coincide con uno degli assi cartesiani e il punto medio di $F_1F_2$ coincide con l’origine, diremo che abbiamo a che fare con un’ellisse centrata nell’origine. Si può mostrare che ciascuna ellisse di questo genere ha un’equazione del tipo: $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \qquad a > 0, \ b > 0$$A seconda del valore che assumono $a$ e $b$ la forma dell’ellisse e le grandezze ad essa relative cambiano di conseguenza. In particolare, si distinguono tre casi:
- $a^2 > b^2$, cioè $\mathbf{a > b}$: in questo caso l’ellisse ha i fuochi sull’asse $x$.

- $a^2 = b^2$, cioè $\mathbf{a = b}$: in questo caso l’ellisse è in realtà una circonferenza (infatti, basta moltiplicare entrambi i membri dell’equazione per $a^2$ per ottenere l’equazione di una circonferenza). In questo caso i fuochi coincidono con il centro della circonferenza, che è l’origine degli assi, e il raggio della circonferenza è lungo $a$.

- $a^2 < b^2$, cioè $\mathbf{a < b}$: in questo caso l’ellisse ha i fuochi sull’asse $y$.

Nella tabella che segue riportiamo le formule principali che riguardano un’ellisse centrata nell’origine. Per alcune di queste formule si vede che la distinzione tra $a > b$ e $a < b$ è essenziale.
| $\mathbf{a>b}$ | $\mathbf{a<b}$ | |
| Fuochi $F_1, F_2$ | $F_1 \equiv (-\sqrt{a^2-b^2}, 0), F_2 \equiv (\sqrt{a^2-b^2}, 0)$ | $F_1 \equiv (0, \sqrt{b^2-a^2}), F_2 \equiv (0, -\sqrt{b^2-a^2})$ |
| Intersezioni con l’asse $x$ | $P \equiv (-a, 0), \ Q \equiv (a,0)$ | $P \equiv (-a, 0), \ Q \equiv (a,0)$ |
| Intersezioni con l’asse $y$ | $R \equiv (0, b), \ S \equiv (0, -b)$ | $R \equiv (0, b), \ S \equiv (0, -b)$ |
| Eccentricità $e$ | $e = \frac{\sqrt{a^2-b^2}}{a}$ | $e = \frac{\sqrt{b^2-a^2}}{b}$ |
| Asse maggiore | $\overline{PQ} = 2a$ | $\overline{RS} = 2b$ |
| Asse minore | $\overline{RS} = 2b$ | $\overline{PQ} = 2a$ |
| Distanza tra i fuochi | $\overline{F_1F_2} = 2\sqrt{a^2-b^2}$ | $\overline{F_1F_2} = 2\sqrt{b^2-a^2}$ |
Inoltre, l’area di piano compresa all’interno di un’ellisse centrata nell’origine è data dalla seguente formula: $$A = \pi \cdot a \cdot b.$$
Tangenti a un’ellisse
Supponiamo di voler trovare l’equazione delle rette passanti per un punto $T \equiv (x_T, y_T)$ e tangenti a una ellisse centrata nell’origine. Le formule che dobbiamo utilizzare sono differenti a seconda della posizione di $T$.
- Se $T$ è un punto interno all’ellisse, non ci sono rette tangenti.
- Se $T$ è un punto dell’ellisse, allora esiste una sola retta tangente all’ellisse che passa per $T$, la cui equazione è data dalla formula di sdoppiamento:$$r: \quad \frac{x \cdot x_T}{a^2} + \frac{y \cdot y_T}{b^2} = 1$$Sostituendo le coordinate di $T$ e i coefficienti $a, b$ nella formula appena mostrata otteniamo infatti una equazione di primo grado in $x$ e $y$, che rappresenterà proprio la retta che vogliamo noi.
Sottolineiamo che il coefficiente angolare di questa retta è: $$m = -\frac{b^2x_T}{a^2y_T}.$$Possiamo ricavare facilmente questa formula riordinando la formula di sdoppiamento in modo da ottenere una retta in forma esplicita. - Se $T$ è un punto esterno all’ellisse, allora le rette tangenti all’ellisse che passano per $T$ sono due. Anche se non mostriamo i passaggi algebrici in questa lezione, è possibile far vedere che per determinare le rette in questione bisogna ricondursi alla seguente equazione in $m$: $$(a^2 - x_T^2)\mathbf{m}^2 + 2x_Ty_T \mathbf{m} + b^2 - y_T^2=0$$È necessario fare alcune osservazioni:
- se $(a^2 - x_T^2) \neq 0$, l’equazione è di secondo grado in $m$. Se si studia il delta di questa equazione, ci si accorge che la condizione $\Delta > 0$ è automaticamente soddisfatta dal fatto che $T$ è esterno all’ellisse. Le due soluzioni $m_1, m_2$ saranno quindi i coefficienti angolari delle rette tangenti all’ellisse passanti per $T$, che avranno equazioni: $$r_1: \ y-y_T = m_1(x-x_T), \qquad r_2: \ y-y_T = m_2(x-x_T)$$
- se $(a^2 - x_T^2) = 0$, che può accadere quando $x_T = a$ oppure $x_T = -a$ (cioè, quando l’ascissa di $T$ è la stessa di una delle intersezioni dell’ellisse con l’asse $x$), allora l’equazione è di primo grado in $m$. Da essa quindi otterremo solo una soluzione $m_1$, ma questo non significa che l’altra retta tangente sia sparita: infatti le rette sono sempre due, e sono date dalle formule: $$r_1: \ y-y_T = m_1(x-x_T), \qquad r_2: x = x_T$$

Formule per un’ellisse traslata
Applicando una traslazione a un’ellisse centrata nell’origine, otteniamo nuovamente un’ellisse con assi paralleli agli assi cartesiani. Essa avrà un’equazione di questo tipo: $$\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1$$dove $x_0$ e $y_0$ sono le coordinate del vettore che stiamo utilizzando per traslare l’ellisse e, come prima, $a$ e $b$ sono numeri reali positivi qualunque.

Quando siamo a conoscenza del valore di $x_0$ e $y_0$ è facile ottenere le formule relative ad un’ellisse traslata. Infatti, tutte le quantità che sono riconducibili alle proprietà geometriche di un’ellisse rimangono invariate, come l’eccentricità, la distanza tra i fuochi, l’area $A$ e così via. Cambiano invece le coordinate dei fuochi: $$F_1 \equiv \begin{cases} (-\sqrt{a^2-b^2}+x_0, y_0) \ \text{se }a>b \\ (x_0, -\sqrt{b^2-a^2}+y_0) \ \text{se }a<b \end{cases} \quad F_2 \equiv \begin{cases} (\sqrt{a^2-b^2}+x_0, y_0) \ \text{se }a>b \\ (x_0, -\sqrt{b^2-a^2}+y_0) \ \text{se }a<b \end{cases}$$Quando consideriamo un’ellisse traslata non ha più molto senso considerare le coordinate delle intersezioni dell’ellisse con gli assi cartesiani, dato che potrebbero non esserci nemmeno. Ha senso comunque considerare i vertici dell’ellisse, che sono i punti in cui l’ellisse ha tangenti orizzontali e verticali, che hanno le seguenti coordinate: $$P \equiv (-a+x_0, y_0),\ Q \equiv (a+x_0, y_0), \ R \equiv (x_0, b+y_0), \ S \equiv (x_0, -b+y_0)$$
Nel caso si volesse trovare l’equazione di una retta tangente passante per un certo punto $T$ a una ellisse traslata, invece, bisognerà ricorrere al metodo esposto per una ellisse centrata nell’origine con gli stessi $a$ e $b$, avendo cura di traslare $T$ adeguatamente, per poi ritraslare la retta ottenuta dello stesso vettore di cui è traslata l’ellisse. Alternativamente, si può impostare il sistema di secondo grado: $$ \begin{cases} \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 \\ y-y_T = m(x-x_T) \end{cases}$$e imporre $\Delta =0$ nell’equazione di secondo grado risolutiva.