Quando definiamo matematicamente un insieme, è a volte utile ricorrere all’utilizzo della cosiddetta rappresentazione intensiva: si descrive un insieme a partire dalla proprietà caratteristica che i suoi elementi soddisfano.
Nell’ambito della Geometria si può fare la stessa cosa: per esempio, all’interno dei punti del piano possiamo considerare l’insieme di tutti quei punti che soddisfano una o più proprietà che imponiamo noi.
Definizione
Un insieme di punti del piano definito in maniera intensiva, cioè a partire da una o più proprietà caratteristiche, è detto luogo geometrico, o anche luogo di punti, o più semplicemente luogo.
Forse la definizione che abbiamo dato è un po’ generica, e non è molto chiara; facciamo qualche esempio “famoso” per capirci meglio. In questi esempi il piano verrà indicato con la lettera $E$.
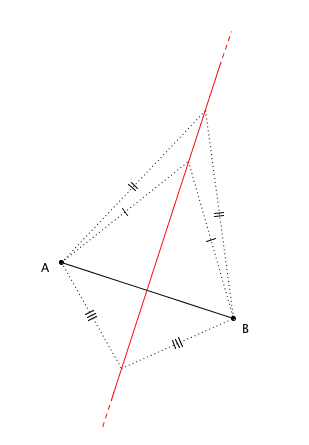
- Prendiamo un segmento $AB$ e consideriamo il luogo $a$ costituito dai punti che hanno la stessa distanza da $A$ e da $B$: ovvero $$a = \left \{ P \in E \ \big | \ \overline{PA} = \overline{PB} \right \}$$L’insieme $a$ è chiamato asse del segmento $AB$.
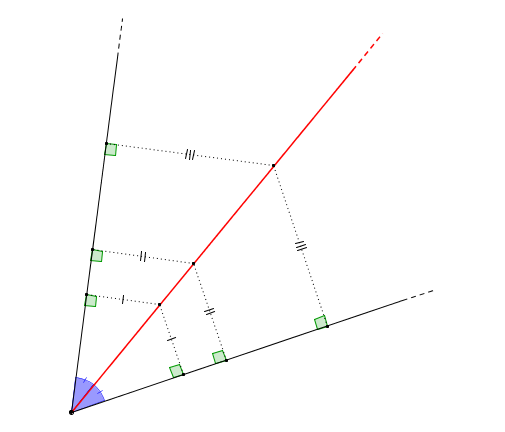
- Consideriamo due semirette $r$ e $s$ con la stessa origine, e consideriamo un angolo $\alpha$ determinato da esse. Definiamo un luogo geometrico $b$ in questo modo: $$b = \left \{ P \in \alpha\ \big | \ dist(P, r) = dist(P, s) \right \}$$Si può mostrare che il luogo $b$ è proprio la bisettrice dell’angolo $\alpha$.
- Il luogo dei punti equidistanti dai lati di un triangolo si riduce a un solo punto: l’incentro del triangolo considerato.
- Scegliamo un punto $C$ nel piano $E$, e prendiamo un numero positivo $r > 0$. Definiamo un insieme $A$ in questo modo: $$A = \left \{ P \in E \ \big | \ \overline{CP} = r \right \}$$Stiamo cioè considerando il luogo geometrico $A$ dei punti di $E$ che distano esattamente $r$ dal punto $C$ che abbiamo scelto. Sappiamo che questo insieme è proprio una circonferenza di centro $C$ e di raggio $r$.
Sottolineiamo che anche l’ellisse, la parabola e l’iperbole possono essere definiti come luoghi geometrici nel piano.
Dagli esempi che abbiamo fatto si vede come un luogo geometrico possa essere una retta, una curva o persino un punto. In effetti quando definiamo un luogo stiamo definendo semplicemente un insieme di punti, e non c’è nessuna buona ragione per pensare che un insieme di punti abbia una forma “privilegiata”.
Luoghi geometrici in Geometria Analitica: l’asse di un segmento
È molto interessante ricavare una rappresentazione dei luoghi geometrici studiandoli dal punto di vista della Geometria Analitica. Per fare questo, esiste una sorta di procedimento generale, che consiste di due passi:
- considerare un “punto generico” $P \equiv (x, y)$ del luogo e imporre che $P$ rispetti la condizione che definisce il luogo geometrico, ottenendo una condizione algebrica su $x$ e $y$;
- esprimere la condizione ottenuta al passo precedente nella forma più “bella” possibile.
Applichiamo il procedimento per ottenere la formula che rappresenta l’asse $a$ di un segmento $AB$ a partire dalle coordinate dei suoi estremi $A \equiv ( x_A, y_A)$ e $B \equiv ( x_B, y_B)$.
- Preso un punto qualsiasi $P \equiv (x, y)$, dobbiamo imporre che esso rispetti la condizione che definisce il luogo geometrico. Valgono le seguenti formule, che esprimono la distanza tra i punti $P$ e $A, B$ rispettivamente:
##KATEX##\begin{aligned}\overline{AP} & = \sqrt{(x_A - x)^2 + (y_A - y)^2} \\\overline{BP} & = \sqrt{(x_B - x)^2 + (y_B - y)^2}\end{aligned}##KATEX##
Il punto $P$ appartiene all’asse del segmento se e solo se $\overline{AP} = \overline{BP}$; quindi, la condizione algebrica che definisce il nostro luogo geometrico è $$a: \quad \sqrt{(x_A - x)^2 + (y_A - y)^2} = \sqrt{(x_B - x)^2 + (y_B - y)^2}.$$ - Prendiamo la condizione ottenuta prima, e proviamo sistemarla un po’. Possiamo innanzitutto elevare al quadrato entrambi i membri dell’equazione, dato che sono non negativi: ##KATEX##\begin{aligned}\sqrt{(x_A - x)^2 + (y_A - y)^2} & = \sqrt{(x_B - x)^2 + (y_B - y)^2} \\(x_A - x)^2 + (y_A - y)^2 & = (x_B - x)^2 + (y_B - y)^2 \\x_A^2 - 2xx_A +x^2 + y_A^2 - 2yy_A +y^2 & = x_B^2 - 2xx_B +x^2 + y_B^2 - 2yy_B +y^2 \\2(x_B - x_A)x + 2(y_B - y_A)y + & x_A^2 - x_B^2 + y_A^2 - y_B^2 = 0\end{aligned}##KATEX##L’equazione ottenuta è quella di una retta, espressa in forma implicita (ricordiamo infatti che $x$ e $y$ sono incognite, mentre $x_A, y_A, x_B, y_B$ sono numeri). Se $y_B \neq y_A$, possiamo esprimere questa retta anche in forma esplicita: $$a : y = - \frac{x_B - x_A}{y_B - y_A} x - \frac{y_A + y_B}{2} + \frac{x_A^2 - x_B^2}{2(y_B - y_A)}$$Di questa retta è importante notare che il coefficiente angolare $$m_a = - \frac{x_B - x_A}{y_B - y_A}$$è proprio il reciproco dell’opposto del coefficiente angolare del segmento $AB$, in linea con il fatto che l’asse di un segmento è sempre perpendicolare a esso.