In questa lezione, diamo la definizione e mostriamo alcune importanti proprietà dei cosiddetti punti notevoli di un triangolo. Questi punti si ricavano a partire dal triangolo considerato tramite alcune operazioni geometriche. Di solito si tratta di intersecare alcuni segmenti e/o rette opportunamente scelti.
Per seguire al meglio questa lezione, è necessario avere chiara la nozione di triangolo e i principali concetti della geometria euclidea di base.
Mediane e baricentro
Consideriamo un triangolo $ABC$ ed individuiamo il punto medio di ciascun lato. Ogni punto medio così ottenuto può essere collegato con un segmento al vertice opposto.
Definizione
Si chiama mediana relativa ad un lato di un triangolo il segmento ottenuto collegando il punto medio del lato considerato con il vertice opposto al lato.
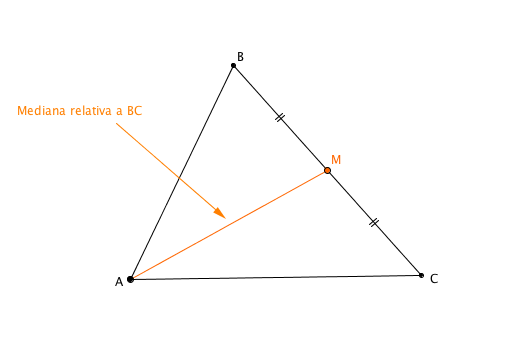
Nel disegno precedente abbiamo tracciato il segmento $AM$, che è la mediana relativa a $BC$ nel triangolo $ABC$. A seconda del lato scelto, otteniamo una mediana: quindi ogni triangolo ha sempre tre mediane.
Le mediane hanno le seguenti proprietà:
- Ogni mediana divide il triangolo in due triangoli equivalenti. Riferendoci alla figura precedente, abbiamo quindi $Area(ABM) = Area(MAC)$.
- Le mediane di un triangolo si incontrano tutte nello stesso punto.
Definizione
Il punto di incontro delle tre mediane di un triangolo è detto baricentro del triangolo.

Elenchiamo qui alcune proprietà del baricentro:
- esso divide la mediana in due segmenti: il segmento che ha per estremo un vertice del triangolo è il doppio dell’altro (nella figura precedente, ad esempio: $AO \cong 2OM$).
- è sempre un punto interno al triangolo.
Altezze e ortocentro
Dato un triangolo $ABC$ consideriamo le tre possibili altezze che possiamo costruire relativamente a ciascun lato. Si dimostra che le altezze si incontrano tutte in un medesimo punto.
Definizione
Si chiama ortocentro di un triangolo il punto di incontro delle altezze relative ai lati del triangolo considerato.

La posizione dell’ortocentro può essere messa in relazione con le caratteristiche degli angoli di un triangolo.
- L’ortocentro è un punto interno al triangolo se e solo se il triangolo è acutangolo.
- L’ortocentro è un punto esterno al triangolo se e solo se il triangolo è ottusangolo.
- L’ortocentro coincide con uno dei vertici del triangolo se e solo se il triangolo è rettangolo (e in questo caso l’ortocentro coincide con il vertice corrispondente all’angolo retto).

Assi e circocentro
Consideriamo nuovamente un triangolo $ABC$ e costruiamo i tre assi relativi ai tre lati del triangolo. Queste tre rette si intersecano nello stesso punto (fatto non banale, ma che si può dimostrare).
Definizione
Si chiama circocentro di un triangolo il punto di incontro delle assi relative ai lati del triangolo considerato.

Tra le proprietà del circocentro, ricordiamo che:
- è il centro della circonferenza circoscritta al triangolo;
- è equidistante dai vertici del triangolo (segue dalla proprietà precedente).
Come accade per l’ortocentro, la sua posizione determina le caratteristiche degli angoli del triangolo. In particolare:
- il circocentro è un punto interno al triangolo se e solo se il triangolo è acutangolo;
- il circocentro è un punto esterno al triangolo se e solo se il triangolo è ottusangolo;
- il circocentro è il punto medio di uno dei lati se e solo se il triangolo è rettangolo (ed in questo caso il lato in questione è l’ipotenusa del triangolo).
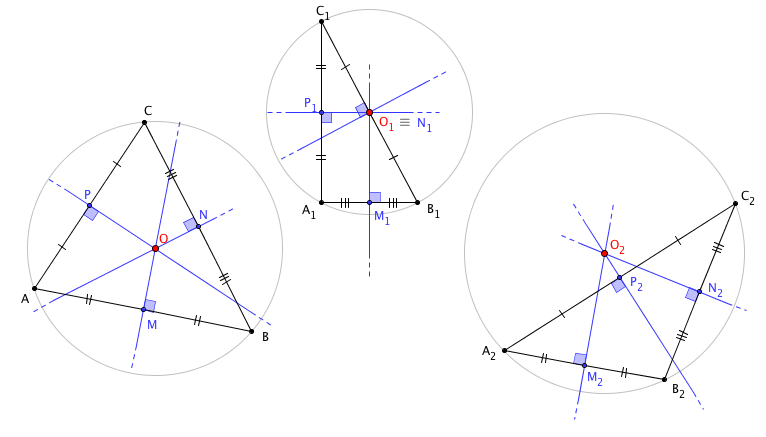
Curiosità.
Il circocentro, il baricentro e l'ortocentro di un triangolo equilatero sono coincidenti. Se il triangolo non è equilatero, tuttavia, questi tre punti notevoli hanno una interessante proprietà: essi sono sempre allineati, ovvero giacciono sulla medesima retta. Questa retta viene chiamata retta di Eulero.
Bisettrici e incentro
Nel triangolo $ABC$ consideriamo le tre bisettrici degli angoli $\widehat{BAC}, \widehat{ABC}$ e $\widehat{BCA}$. È possibile dimostrare che esse si incontrano in un solo punto.
Definizione
Si chiama incentro di un triangolo il punto di incontro delle bisettrici degli angoli interni al triangolo considerato.

Elenchiamo alcune proprietà dell’incentro.
- È sempre un punto interno al triangolo.
- È il centro della circonferenza inscritta nel triangolo.
- Come conseguenza della proprietà precedente, la distanza dell’incentro da un lato del triangolo è la stessa, indipendentemente da lato scelto.
- Ogni bisettrice divide il triangolo considerato in due triangoli più piccoli. Consideriamone uno (per esempio $BCP$ nella figura qui sopra) e prendiamo il lato costituito dalla bisettrice. L’incentro divide questo lato in due segmenti. La proporzione tra questi segmenti è la stessa che c’è tra gli altri due lati del triangolo considerato. Nel caso del triangolo $BCP$: $BI:IP = BC:CP$. Lo stesso discorso può essere ripetuto per il triangolo $ABP$, ottenendo $BI:IP = AB:AP$.
Curiosità.
L'incentro di un triangolo equilatero coincide con gli altri tre punti notevoli. Inoltre, l'incentro di un triangolo isoscele giace sulla retta di Eulero (definita più sopra). Se consideriamo un triangolo che non sia né equilatero né isoscele, invece, l'incentro non è mai allineato con circocentro, baricentro e ortocentro.
Gli excentri
In un triangolo $ABC$, consideriamo le bisettrici di due angoli esterni al triangolo (per esempio l’angolo esterno a $\widehat{ABC}$ e quello esterno a $\widehat{BCA}$). Queste due bisettrici si incontrano in un punto esterno al triangolo (nel nostro esempio, il punto $E$). Per questo punto passa anche la bisettrice dell’angolo interno non adiacente agli angoli presi in considerazione (nel nostro caso $\widehat{CAB}$). Tale punto viene detto excentro.

Possiamo fare alcune osservazioni.
- A seconda della scelta degli angoli che consideriamo, abbiamo un excentro diverso. Infatti, a ogni triangolo possiamo associare tre differenti excentri.
- Ogni excentro è equidistante dalle rette determinate dai lati del triangolo (questa proprietà è del tutto analoga a quella dell’incentro).
- Ogni excentro è il centro di una circonferenza che ha per tangenti un lato del triangolo e i prolungamenti degli altri due (anche qui, in analogia con l’incentro).

Revisione scientifica a cura di Marco Guglielmino