Una volta definiti i concetti di retta e segmento, possiamo costruire figure più complesse a partire da questi. Per esempio, immaginiamo di collegare tra loro dei punti sul piano con dei segmenti, in modo che:
- i segmenti non si intersechino mai fra loro;
- ogni punto sia collegato sempre a due altri punti.
Abbiamo appena costruito un poligono, che è uno tra gli oggetti più comuni della Geometria euclidea. Ma affrontiamo ora l’argomento in maniera più rigorosa.
Definizione
La figura formata da più segmenti consecutivi si chiama poligonale aperta. I segmenti si dicono lati della spezzata e i loro estremi vertici.
Se a una poligonale aperta si aggiunge il segmento che ne congiunge gli estremi, otteniamo una poligonale chiusa.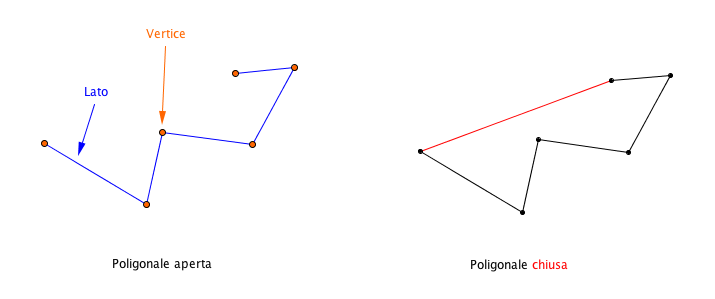
Definizione
Un poligono è la figura formata da una poligonale chiusa e dalla parte di piano che essa delimita.
ATTENZIONE: Per la nostra trattazione, consideremo solamente poligonali che non si auto-intersecano (cioè, escludiamo le cosiddette poligonali intrecciate).
I vertici e i lati della poligonale che definisce un poligono si diranno nuovamente vertici e lati. I punti del poligono che non appartengono alla poligonale si dicono punti interni; tutti i punti che non appartengono al poligono si dicono punti esterni. I segmenti della poligonale costituiscono il perimetro del poligono.

Definizione
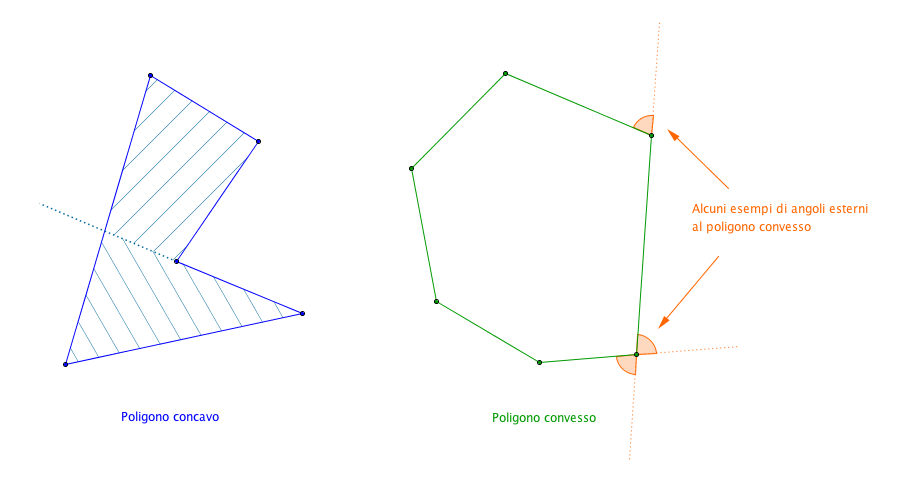
Un poligono viene detto concavo se il prolungamento di uno dei suoi lati lo divide in due parti, mentre viene detto convesso se questo non accade per nessun lato.
Gli angoli convessi formati dalle coppie di lati consecutivi di un poligono convesso si dicono angoli interni (molto spesso si chiameranno solo angoli del poligono). Gli angoli adiacenti agli angoli interni si dicono angoli esterni del poligono convesso.
Sottolineiamo che in un poligono è sufficiente individuare un solo lato il cui prolungamento divida in due parti il poligono stesso, per stabilire che è concavo; invece, un poligono è convesso se i prolungamenti di tutti i lati non lo dividono in due parti.
ATTENZIONE: Da ora in poi, per semplicità, considereremo solamente poligoni convessi, riferendoci a essi semplicemente come “poligoni”.
La classificazione più rapida che possiamo stabilire all’interno dell’insieme dei poligoni è basata sul conteggio dei suoi lati. Avremo quindi, per esempio:
- i poligoni di 3 lati, detti triangoli;
- i poligoni di 4 lati, detti quadrilateri;
- i poligoni di 5 lati, detti pentagoni;
- i poligoni di 6 lati, detti esagoni;
e così via, anche se possiamo fare riferimento alla dicitura più generale di poligono di $n$ lati.
Ciascuna di queste categorie può essere analizzata molto nel dettaglio, specialmente per quanto riguarda i triangoli (che costituiscono una sorta di “fondamento” della costruzione dei poligoni).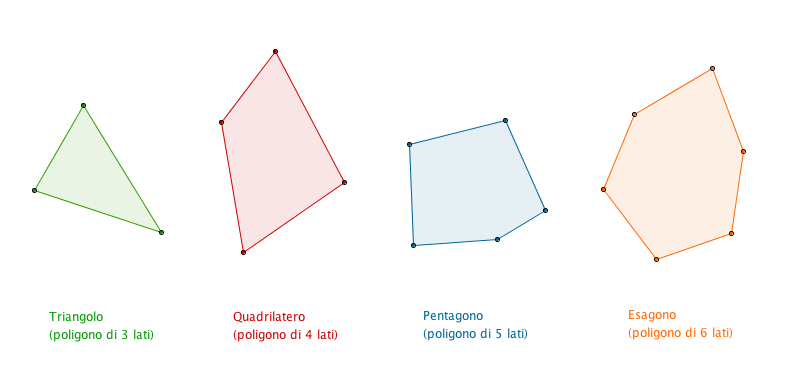
Particolare importanza avranno anche i poligoni regolari, ovvero quei poligoni che hanno tutti i lati e tutti gli angoli congruenti tra loro. Per esempio:
- il triangolo equilatero;
- il quadrato;
- il pentagono regolare;
- l’esagono regolare;
e così via. In generale si può sempre fare riferimento a un poligono regolare di $n$ lati.
Definizione
Un segmento che ha per estremi due punti del perimetro di un poligono (non appartenenti allo stesso lato) è detto corda del poligono.
Una corda che ha per estremi due vertici non consecutivi di un poligono è detta diagonale del poligono.
Facciamo notare che:
- un triangolo non ha diagonali;
- un quadrilatero ha due diagonali;
- in generale, un poligono di $n$ lati ha $\frac{n(n-3)}{2}$ diagonali.

Come ultima cosa, enunciamo un importante teorema riguardo ai poligoni:
TEOREMA: la somma degli angoli interni di un poligono di $n$ lati è $\pi(n-2)$ radianti, o $180(n-2)$ gradi.
Revisione scientifica a cura di Marco Guglielmino