Un poligono avente tre lati è detto triangolo. È una delle figure geometriche più famose e sicuramente una delle più analizzate, a causa della sua importanza nello sviluppo di altre figure geometriche. In questa lezione esporremo le proprietà e le definizioni di base relative al triangolo e ai suoi elementi che lo caratterizzano.
Definizione
Ciascuno dei segmenti che compongono un triangolo viene detto lato del triangolo, mentre ciascuno degli estremi dei segmenti viene detto vertice. Ciascun vertice viene considerato in maniera naturale come vertice di un angolo del triangolo (spesso chiamato anche angolo interno). I lati e gli angoli di un triangolo vengono detti elementi del triangolo.
Ogni lato viene detto:
- opposto al vertice che non gli appartiene (e l’angolo che ha quel vertice è detto ancora opposto al lato);
- adiacente agli angoli che hanno come vertice un suo estremo.

Notazione: i punti che rappresentano i vertici del triangolo si indicano con una lettera maiuscola dell’alfabeto latino ($A, B, C \ldots $) e gli angoli invece con una lettera minuscola dell’alfabeto greco ($\alpha, \beta, \gamma \ldots$). Come evidenziato in figura, si preferisce far corrispondere lettere greche e lettere latine (ad $A$ corrisponde $\alpha$, a $B$ corrisponde $\beta$, a $C$ corrisponde $\gamma$). Spesso, inoltre, i lati vengono indicati con lettere minuscole dell’alfabeto latino ($a, b, c \ldots$) in modo tale che ci sia corrispondenza tra lati e vertici opposti (ad $A$ è opposto $a$, a $B$ è opposto $b$, a $C$ è opposto $c$).
Definizione (classificazione dei triangoli in base ai lati)
Dato un triangolo, diremo che esso è:
- isoscele se due dei suoi lati sono congruenti;
- equilatero se ha tutti e tre i lati congruenti;
- scaleno in tutti gli altri casi.

Definizione (classificazione dei triangoli in base agli angoli)
Dato un triangolo, diremo che esso è:
- acutangolo se tutti i suoi angoli sono acuti;
- ottusangolo se ha un angolo ottuso;
- rettangolo se ha un angolo retto.
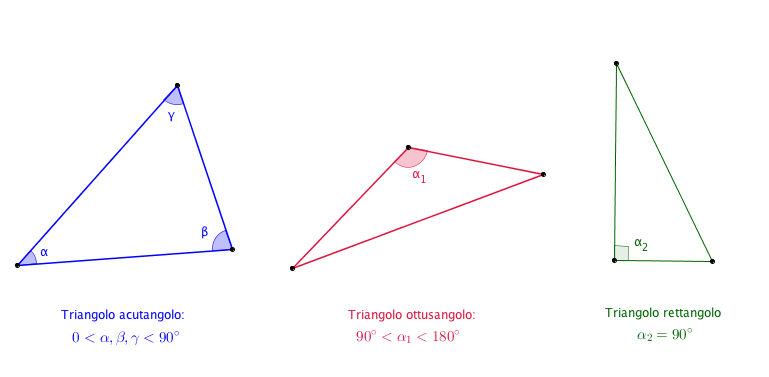
Nella definizione precedente non si fa riferimento alla situazione in cui il triangolo possa avere più di un angolo ottuso, o più di un angolo retto. Inoltre, essendo una classificazione, si sottointende che un triangolo non possa avere contemporaneamente un angolo retto e un angolo ottuso (altrimenti sarebbe allo stesso tempo ottusangolo e rettangolo). Basta prendere carta e penna per accorgersi che non è possibile disegnare un triangolo con le caratteristiche proposte; infatti, vale il seguente
TEOREMA: In un triangolo vi sono sempre almeno due angoli acuti.
Questo giustifica il fatto che la definizione appena data sia a tutti gli effetti una classificazione.
Definizione
Consideriamo un vertice di un triangolo, e tracciamo la distanza di questo vertice dalla retta che contiene il lato opposto. Il segmento così ottenuto viene chiamato altezza relativa al lato considerato.

Dalla definizione appena data ci accorgiamo che per ogni triangolo esistono tre altezze, una relativa a ogni lato (oppure, ciascuna costruita a partire da un vertice diverso).
Quando si considera un triangolo rettangolo, l’altezza relativa a un cateto coincide con l’altro cateto. Se invece consideriamo un triangolo ottusangolo, le altezze relative ai lati dell’angolo ottuso sono sempre esterne ai lati considerati (si veda la figura qui sotto).
Elenchiamo adesso alcune proprietà che un triangolo qualunque possiede; ciascuna di esse può essere dimostrata, ma in questa lezione ci limitiamo a enunciarle.
- Ogni angolo esterno è congruente alla somma dei due angoli interni non adiacenti a esso.
- La somma degli angoli interni è pari a un angolo piatto.
- Se due lati sono diseguali, anche gli angoli opposti saranno diseguali (e viceversa). Inoltre, al lato maggiore sta opposto l’angolo maggiore.
- Ciascun lato è minore della somma degli altri due (disuguaglianza triangolare).
- Ciascun lato è maggiore della differenza degli altri due (disuguaglianza triangolare inversa).
Revisione scientifica a cura di Marco Guglielmino