Tra i vari tipi di triangolo che si possono considerare, assume una particolare importanza il triangolo isoscele. Vediamo infatti che, imponendo una semplicissima proprietà (il fatto di avere due lati congruenti), si ottengono sorprendenti risultati geometrici e formule molto eleganti.
Definizione
Chiamiamo triangolo isoscele un triangolo che ha due lati congruenti.
Il lato che non è congruente agli altri due si chiama base.
Gli angoli adiacenti alla base si dicono angoli alla base del triangolo mentre l’angolo rimanente viene chiamato angolo al vertice del triangolo.
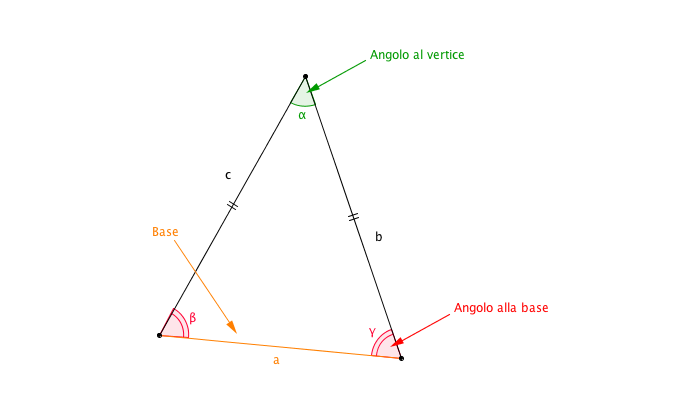
Un triangolo isoscele ha le seguenti proprietà:
- Un triangolo è isoscele se e solo se gli angoli alla base sono congruenti. Inoltre gli angoli alla base del triangolo sono sempre acuti.
- In un triangolo isoscele l’altezza relativa alla base, la mediana relativa alla base, l’asse della base e la bisettrice dell’angolo al vertice giacciono tutte sulla stessa retta. Inoltre, la mediana e l'altezza relative alla base sono congruenti.
- Le altezze relative ai lati congruenti tra loro sono a loro volta congruenti, così come le mediane relative a tali lati.
- Ortocentro, baricentro, circocentro e incentro giacciono tutti sulla stessa retta (che è la stessa su cui giace l’altezza relativa alla base, per esempio).
Per conoscere le grandezze relative a un triangolo isoscele è sufficiente avere a disposizione le misure di:
- un lato e un angolo qualsiasi;
- la base e un altro lato.
Nel seguito questi casi vengono ulteriormente suddivisi, a seconda che si conosca la misura della base o di uno dei lati congruenti, o la misura degli angoli alla base o dell'angolo al vertice.
Per avere una comprensione soddisfacente delle formule in cui si utilizzano le misure degli angoli, si richiede una conoscenza approfondita della trigonometria e delle sue applicazioni ai triangoli (le formule sono state inserite per ragioni di completezza, nonostante non siano strettamente inerenti alla Geometria Euclidea).
ATTENZIONE: D'ora in poi, quando parleremo di un triangolo isoscele faremo sempre riferimento ai nomi dei lati e degli angoli dati nella figura in alto.
Area e perimetro

Raggi

Segmenti notevoli per il triangolo
Per questa sezione, utilizzeremo la seguente convenzione: indichiamo rispettivamente con $h_l$ e $m_l$ l'altezza e la mediana relativa a uno dei lati $c$ e $b$ (possiamo non distinguere le due mediane e le due altezze poiché sono congruenti). L'altezza e la mediana relativa alla base invece saranno indicate con $h_a$ e $m_a$.

Elementi mancanti del triangolo

Revisione scientifica a cura di Marco Guglielmino