Come si fa a capire se due triangoli sono congruenti? Un metodo può essere quello di controllare che tutti gli angoli e tutti i lati di un triangolo siano congruenti a ciascun altro lato e angolo dell’altro: di certo questo procedimento funziona, ma non è per niente rapido, e spesso poco fattibile (non sempre si hanno a disposizione tutte le informazioni necessarie).
Per risolvere questo problema sono stati introdotti i cosiddetti criteri di congruenza per i triangoli, con i quali è possibile capire - a partire da (relativamente) poche informazioni - se due triangoli sono congruenti. Ciascun criterio, quindi è una condizione sufficiente per stabilire se due triangoli sono congruenti.
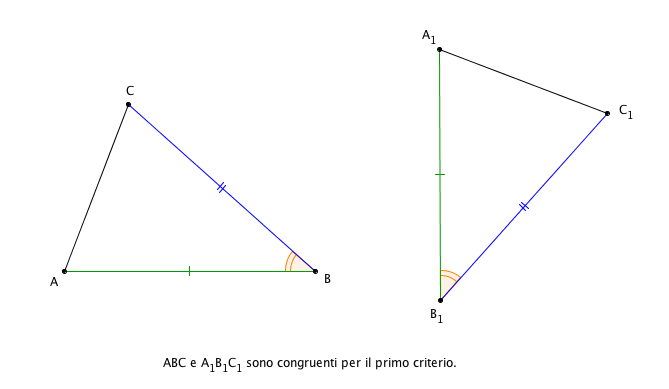
TEOREMA (Primo criterio di congruenza): Se due triangoli hanno rispettivamente congruenti due lati e l’angolo tra essi compreso, allora sono congruenti.
TEOREMA (Secondo criterio di congruenza): Se due triangoli hanno rispettivamente congruenti due angoli e il lato tra essi compreso, allora sono congruenti.

TEOREMA (Terzo criterio di congruenza): Se due triangoli hanno rispettivamente congruenti tutti e tre i lati, allora sono congruenti.

Come si può notare, nel primo criterio si specifica che l’angolo congruente deve essere compreso tra i due lati rispettivamente congruenti. In modo analogo nel secondo criterio si specifica che il lato congruente deve essere compreso tra i due angoli rispettivamente congruenti. Sono davvero necessarie queste richieste? In altre parole ci chiediamo:
- se due triangoli hanno due lati e un qualsiasi angolo rispettivamente congruenti, allora sono congruenti?
- se due triangoli hanno due angoli e un qualsiasi lato rispettivamente congruenti, allora sono congruenti?
La risposta alla prima domanda è, in generale, NO. Infatti vediamo nel prossimo disegno che i due triangoli dati hanno le caratteristiche richieste, ma non sono congruenti:

Si può dimostrare però il seguente risultato:
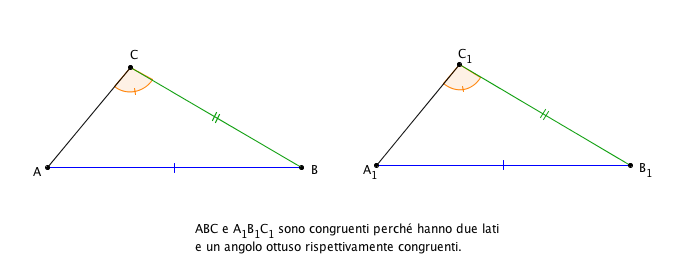
TEOREMA (Primo criterio di congruenza “speciale”): Se due triangoli hanno rispettivamente congruenti due lati e un angolo, e
- l’angolo è compreso tra i lati, oppure
- l’angolo non è compreso tra i lati ma non è acuto,
allora essi sono congruenti.
La risposta alla seconda domanda, invece, è SI’. Infatti vale il seguente risultato:
TEOREMA (Secondo criterio generalizzato): Se due triangoli hanno rispettivamente congruenti due angoli e un lato, allora sono congruenti.

Conclusione
Possiamo riassumere la situazione in questo modo: due triangoli sono congruenti se hanno congruenti rispettivamente:
- due lati e un angolo qualsiasi non acuto;
- due lati e l’angolo tra essi compreso;
- due angoli e un lato qualsiasi;
- tre lati.
Revisione scientifica a cura di Marco Guglielmino