Definizione
L'iperbole è una curva appartenente alla famiglia delle sezioni coniche (o, semplicemente, coniche), insieme a parabola e ellisse (e circonferenza, caso particolare di ellisse).
Si tratta di curve piane di secondo grado che si ottengono - da qui l'origine del nome - dalle sezioni di un cono con un piano. In particolare, l'iperbole si ottiene sezionando un cono con un piano parallelo al suo asse.

Si chiama iperbole il luogo geometrico dei punti del piano per i quali la differenza delle distanze da due punti fissi detti fuochi si mantiene costante in valore assoluto.
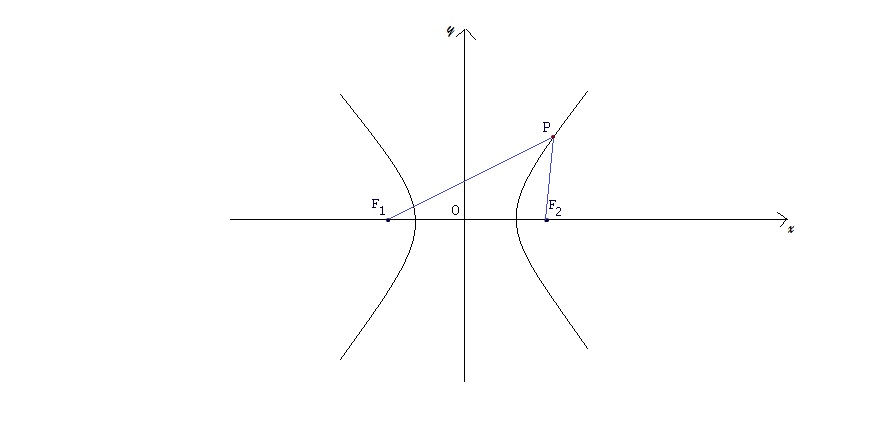
Se poniamo uguale a $2a$ il valore della costante, la definizione si traduce nella scrittura che segue: $$ | \bar{PF_1} - \bar{PF_2} | = 2a $$
La presenza del valore assoluto determina la presenza di due rami per questa curva. Infatti, se $\bar{PF_1} > \bar{PF_2}$, il ramo dell'iperbole, nella figura sopra, è quello di destra e l'equazione corrispondente è: $$ \bar{PF_1} - \bar{PF_2} = 2a $$
Se invece $\bar{PF_1} < \bar{PF_2}$ il ramo dell'iperbole, nella figura sopra, è quello di sinistra e l'equazione corrispondente è: $$ \bar{PF_2} - \bar{PF_1} = 2a $$
L'argomento del valore assoluto è, in questo caso, negativo e va cambiato il segno.
Equazione in forma normale e formulari
Cerchiamo l'equazione dell'iperbole sul piano cartesiano in forma normale e ci poniamo in condizioni particolari, ma che rendono i calcoli più semplici. Come nella figura sopra, poniamo i fuochi sull'asse delle $x$, il centro dell'iperbole nell'origine degli assi, gli assi cartesiani come assi di simmetria. Sia $2c$ la distanza focale: $F_1 \equiv (-c;0)$ e $F_2 \equiv (c;0)$
Applicando la formula della distanza tra due punti, e prendendo in considerazione il punto generico $P \equiv (x;y)$, la definizione dell'iperbole diventa: $$ |\sqrt{(x + c)^2 + y^2} - \sqrt{(x - c)^2 + y^2} | = 2a$$
Svolgendo i calcoli e ponendo $b^2 = c^2 - a^2 > 0$ si arriva all'equazione $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
che prende il nome di equazione in forma normale (o in forma canonica) dell'iperbole con fuochi sull'asse $x$. Allo stesso modo si procede se i fuochi si trovano sull'asse $y$, scambiando i ruoli di $x$ ed $y$ nella precedente equazione. Riassumiamo le definizioni principali e le formule nei due casi con due tabelle.
Iperbole con i fuochi sull'asse $x$
|
Equazione in forma normale (o canonica) |
$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $ |
| Fuochi | $F_1 \equiv (-c;0) = (-\sqrt{a^2 + b^2}; 0)$ $F_2 \equiv (c;0) = (\sqrt{a^2 + b^2}; 0) $ |
| Distanza focale (distanza tra i fuochi) | $2c$ |
| Parametri $a$, $b$ e $c$ | $c>a, c^2 = a^2 + b^2$ |
| Assi di simmetria |
asse $x$: contenente i fuochi |
| Centro di simmetria | $(0; 0)$ punto di intersezione degli assi di simmetria |
| Vertici (punti in cui l'iperbole interseca l'asse contenente i fuochi) |
Intersezione con l'asse $x$ $(y=0)$ $ A_1 \equiv (-a; 0)$ e $ A_2 \equiv (a; 0)$ |
| Asse trasverso (segmento che ha i vertici agli estremi) | $2a$ (la costante della definizione) |
| Eccentricità = rapporto tra distanza focale e asse trasverso ($e>1$) | $ e = \frac{2c}{2a} = \frac{c}{a} $ |
| Asintoti | $ y = \pm \frac{b}{a} x $ |
Iperbole con i fuochi sull'asse y
|
Equazione in forma normale (o canonica) |
$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $ |
| Fuochi | $F_1 \equiv (0;-c) = (0; -\sqrt{a^2 + b^2})$ $F_2 \equiv (0;c) = (0; \sqrt{a^2 + b^2}) $ |
| Distanza focale (distanza tra i fuochi) | $2c$ |
| Parametri $a$, $b$ e $c$ | $c>b, c^2 = b^2 + a^2 $ |
| Assi di simmetria |
asse $y$: contenente i fuochi |
| Centro di simmetria | $(0; 0)$ punto di intersezione degli assi di simmetria |
| Vertici (punti in cui l'iperbole interseca l'asse contenente i fuochi) |
Intersezione con l'asse $y$ $(x = 0)$ $ B_1 \equiv (0; -b)$ e $ B_2 \equiv (0; b)$ |
| Asse trasverso (segmento che ha i vertici agli estremi) | $2b$ (la costante della definizione) |
| Eccentricità = rapporto tra distanza focale e asse trasverso ($e>1$) | $ e = \frac{2c}{2b} = \frac{c}{b} $ |
| Asintoti | $ y = \pm \frac{b}{a} x $ |
Se $a = b$ l'iperbole si chiama equilatera e gode di particolari proprietà:
Iperbole equilatera con i fuochi sull'asse x
|
Equazione in forma normale (o canonica) |
$x^2 - y^2 = a^2$ |
| Fuochi | $F_1 \equiv (-c;0) = (-a\sqrt{2}; 0)$ $F_2 \equiv (c;0) = (a\sqrt{2}; 0) $ |
| Distanza focale | $2c = 2a\sqrt{2}$ |
|
Eccentricità (costante) |
$ e = \frac{c}{a} = \frac{a\sqrt{2}}{a} = \sqrt{2}$ |
|
Asintoti (costanti e perpendicolari tra loro) |
$y = \pm x$ |
Iperbole equilatera con i fuochi sull'asse y
| Equazione in forma normale (o canonica) | $x^2 - y^2 = a^2$ |
| Fuochi | $F_1 \equiv (0;-c) = (0; -a\sqrt{2})$ $F_2 \equiv (0;c) = (0; a\sqrt{2}) $ |
| Distanza focale | $2c = 2a\sqrt{2}$ |
| Eccentricità (costante) | $ e = \frac{c}{b} = \frac{a\sqrt{2}}{a} = \sqrt{2}$ |
| Asintoti (costanti e perpendicolari tra loro) | $y= \pm x$ |
Se si fa ruotare un'iperbole equilatera di $45^\circ$ si dice che l'iperbole è riferita ai propri asintoti. In questo caso:
- gli assi cartesiani diventano gli asintoti
- le bisettrici dei quadranti diventano gli assi di simmetria

L'equazione diventa $xy = k$
- se $k>0$ l'iperbole si trova su primo e terzo quadrante, come in figura
- se $k<0$ l'iperbole si trova su secondo e quarto quadrante
NB - Se il prodotto di due grandezze si mantiene costante ($xy = k$) vuol dire che tra loro c'è una relazione di proporzionalità inversa.