La sfera, il cilindro, il cono, il tronco di cono

I solidi di rotazione: definizione e proprietà

Si chiama solido ogni porzione di spazio delimitata da una superficie chiusa.

Si tratta di figure geometriche che si estendono nello spazio e hanno tre dimensioni: lunghezza, larghezza e altezza. Possiamo suddividerli in due classi:

• poliedri: la superficie è formata da poligoni appartenenti a piani diversi (come il cubo, parallelepipedo, piramidi, prismi…)
• solidi rotondi: se una parte della superficie chiusa è curva.
  
  

I solidi di rotazione sono solidi rotondi che si possono ottenere facendo ruotare una figura piana. Per esempio un cilindro si può ottenere facendo ruotare un rettangolo attorno a uno dei suoi lati, oppure un cono si può generare facendo ruotare un triangolo rettangolo attorno a uno dei suoi cateti.

L’elemento attorno a cui avviene la rotazione individua una retta che si chiama asse di rotazione.

Cilindro

Definizione: Il cilindro si ottiene dalla rotazione completa di un rettangolo attorno a uno dei suoi lati.

Altezza del cilindro ($h$) = è il lato attorno a cui avviene la rotazione.
Raggio del cilindro ($r$) = è il raggio del cerchio di base, l'altro lato del rettangolo.

Se l'altezza e il diametro di base coincidono ($h = 2r$), il cilindro ¹ si chiama equilatero. In questo caso la superficie laterale è il quadruplo della superficie di base: $$ S_L = 2 \pi \cdot r \cdot 2r = 4 \pi r^2 $$ 

E il volume vale: $$ V = \pi \cdot r^2 \cdot 2 r = 2 \pi r^3 $$

Cono

Definizione: Il cono si ottiene dalla rotazione completa di un triangolo rettangolo attorno a un cateto. 

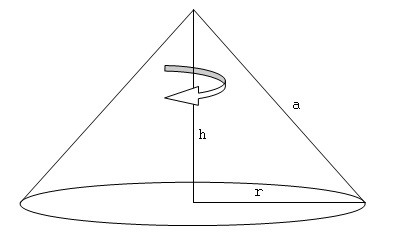
Altezza del cono ($h$) = è il cateto attorno a cui avviene la rotazione.

Raggio del cono ($r$) = è il raggio del cerchio di base, l'altro cateto.
Apotema ($a$) = l'ipotenusa del triangolo rettangolo.

Per il teorema di Pitagora $a$, $r$ e $h$ soddisfano la seguente relazione:

$$ h^2 + r^2 = a^2 $$

Se l'apotema e il diametro di base coincidono ($a = 2r$), il cono ² si chiama equilatero. In questo caso la superficie laterale è il doppio della superficie di base:

$$ S_L = \pi r 2r = 2 \pi r^2 = 2S_B $$

Tronco di Cono

Definizione: Il tronco di cono si ottiene dalla rotazione completa di un trapezio rettangolo attorno al lato perpendicolare alle basi ³.

Altezza ($h$) = è il lato attorno a cui avviene la rotazione.

Raggio maggiore ($R$) = è il raggio del cerchio maggiore di base, la base maggiore del trapezio rettangolo.
Raggio minore ($r$) = è il raggio del cerchio minore di base, la base minore del trapezio rettangolo.
Apotema ($a$)= è il lato obliquo del trapezio rettangolo.

Per il teorema di Pitagora $h$, $R$, $r$ e $a$ soddisfano la relazione:

$$(R - r)^2 + h^2 = a^2 $$

Sfera

Definizione: La sfera si ottiene dalla rotazione completa di un semicerchio attorno al diametro.

La sfera è la figura geometrica solida costituita da tutti i punti dello spazio che distano al più $r$ da un punto fisso, detto centro.

Raggio ($r$) = raggio del semicerchio che compie la rotazione.

Si chiama cerchio massimo il cerchio che si ottiene sezionando una sfera con un piano passate per il centro. Il cerchio massimo e la sfera hanno i centri che coincidono.

Il cilindro circoscritto a una sfera è equilatero e ha:

• superficie laterale coincidente con la superficie della sfera.
• volume pari a $\frac{3}{2}$ quello della sfera.

La sfera è la figura geometrica solida che, a parità di superficie, racchiude il volume più grande.

Facciamo presente che tutte le formule qui ottenute possono essere dedotte mediante il calcolo di opportuni integrali multipli.