Introduzione
In questa lezione cercheremo di generalizzare il concetto di integrale di Riemann di una funzione reale di una variabile reale a funzioni reali di più di una variabile reale. Per la precisione, specializzeremo il concetto per funzioni reali di due e tre variabili reali, ossia funzioni che generalmente possono essere scritte come applicazioni del tipo $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ o $f: \mathbb{R}^3 \longrightarrow \mathbb{R}$. Iniziamo il discorso con funzioni di due variabili.
Integrale di Riemann di funzioni reali di due variabili reali.
Il concetto che l’integrale di Riemann esprime, come abbiamo imparato a conoscerlo nei primi corsi di Analisi, è quello di area (con segno) sottesa al grafico di una funzione. Cerchiamo allora di generalizzare il discorso per funzioni di due variabili reali.
Da qui in avanti, sia $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ la nostra funzione.
Il grafico di $f$ è l’insieme $$ \text{G} (f) = \left\{ (x,y,z) \in \mathbb{R}^3 \ \lvert \ z = f(x,y) \right\}$$Come si vede, è un sottoinsieme di $\mathbb{R}^3$: in generale, se $f$ è una funzione da $\mathbb{R}^n $ a $\mathbb{R}$, $\text{G} (f)$ vive in $\mathbb{R}^{n+1}$. Senza considerare casi patologici, possiamo raffigurarci il grafico di una funzione da $\mathbb{R}^2$ a $\mathbb{R}$ come una superficie nello spazio $\mathbb{R}^3$, in cui la quota $z$ di ciascun punto sulla superficie rappresenta il numero che la funzione $f$ associa alle coordinate $x$ ed $y$ dello stesso punto.
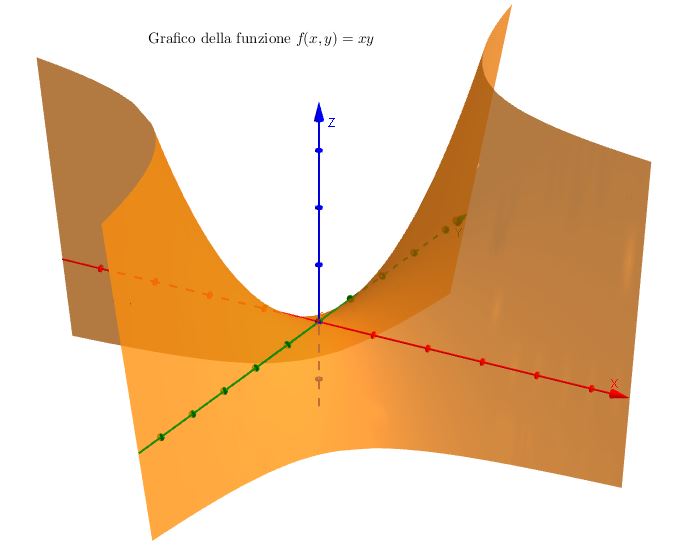
Il nostro scopo sarà quindi di cercare di misurare l’area sottesa a questo grafico.
Integrale di Riemann in due variabili: prima definizione
Naturalmente, $f$ avrà un suo insieme di definizione: per cominciare, consideriamo un caso molto molto particolare, in cui $f$ è definita su un rettangolo chiuso e limitato, con lati paralleli agli assi cartesiani. Chiamiamo questo rettangolo $Q$. È sempre possibile trovare due intervalli reali chiusi e limitati $[a,b]$, $[c,d]$ di modo che $Q$ possa essere scritto come prodotto cartesiano di questi intervalli: $Q = [a,b] \times [c,d]$. Richiediamo inoltre che $f$ sia limitata: senza questa ipotesi, sconfineremmo nell’equivalente bidimensionale degli integrali impropri.

Per funzioni di questo genere, o meglio, per domini di questa forma, la definizione di integrale di Riemann ricalca perfettamente quella che abbiamo fornito per l’integrale di Riemann in una sola variabile: cerchiamo di approssimare il volume sotteso al grafico di $f$ con dei parallelepipedi e, se possiamo migliorare a piacimento questa approssimazione, diremo che la funzione è (Riemann) integrabile su $Q$.
Più rigorosamente, consideriamo la funzione $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ avente insieme di definizione $Q = [a,b] \times [c,d]$. e siano $\mathcal{P}_x$ una partizione dell’intervallo $[a,b]$, costituita dagli intervalli $I_i$, e $\mathcal{P}_y$ una partizione dell’intervallo $[c,d]$, costituita dagli intervalli $J_j$. Sia $\mathcal{P} = \mathcal{P}_x \times \mathcal{P}_y$ la partizione prodotto, fatta da rettangoli $Q_{ij} = I_i \times J_j$, e definiamo i seguenti valori:##KATEX##\begin{aligned} m_{ij} = \text{inf}_{(x,y) \in Q_{ij}} f(x,y) \\ M_{ij} = \text{sup}_{(x,y) \in Q_{ij}} f(x,y) \end{aligned}##KATEX##Sia inoltre $| Q_{ij} |$ l’area del rettangolo $Q_{ij}$. Poniamo le somme inferiori e le somme superiori di $f$ relative alla partizione $\mathcal{P}$ le quantità##KATEX##\begin{aligned} s (f,\mathcal{P}) = \sum_{i,j} m_{ij} | Q_{ij} | \\ S (f,\mathcal{P}) = \sum_{i,j} M_{ij} | Q_{ij} | \end{aligned}##KATEX##Ricordandoci la formula per il volume di un parallelepipedo, $s$ ed $S$ non sono altro che la somma dei volumi dei parallelepipedi, rispettivamente, “piccoli” e “grandi”. Nell’illustrazione qui di seguito, è raffigurato solo un rettangolo $Q_{ij}$, con relativi valori $m_{ij}$ ed $M_{ij}$:

Ora pensiamo di raffinare questa partizione: vogliamo una stima dal basso, rappresentata da $s$, il più alta possibile, mentre una stima dall’alto, che è $S$, il più bassa possibile. Per questo prenderemo l’estremo superiore delle somme inferiori (cioè $\text{sup}_{\mathcal{P}} \left( s(f, \mathcal{P}) \right)$) e l’estremo inferiore delle somme superiori (cioè $\text{inf}_{\mathcal{P}} \left( S(f, \mathcal{P}) \right)$). In generale, al variare della partizione $\mathcal{P}$, otterremo che $\text{sup}_{\mathcal{P}} \left( s(f, \mathcal{P}) \right) \leq \text{inf}_{\mathcal{P}} \left( S(f, \mathcal{P}) \right) $: se queste due stime sono uguali, abbiamo ottenuto il volume sotteso al grafico. Ha senso dunque dire che la funzione $f$, limitata su di un dominio rettangolare $Q$, è Riemann integrabile su $Q$ se, per definizione$$ \text{sup}_{\mathcal{P}} \left( s(f, \mathcal{P}) \right) = \text{inf}_{\mathcal{P}} \left( S(f, \mathcal{P}) \right) $$Questo numero viene detto l’integrale (doppio) di $f$ su $Q$; ci sono molti modi di scrivere questo integrale, ma la notazione che abbiamo scelto di adottare è la seguente:$$ \iint_{Q} f(x,y) dx \ dy $$Altre notazioni equivalenti sono $ \int_{Q} f(x,y) dx \ dy$, $\int_Q f dx \ dy$, o semplicemente $\int_Q f$. Se una funzione è Riemann integrabile su $Q$, si scrive anche $f \in \mathcal{R} (Q)$.
Questa definizione, sebbene sia molto utile per ottenere risultati teorici, è inutilizzabile nella pratica: ci sono troppe condizioni troppo poco agevoli da controllare. Forniamo subito un risultato che garantisce il fatto che una funzione sia Riemann integrabile:
Sia $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione limitata su un dominio rettangolare $Q$. Se $f$ è continua su $Q$, allora $f$ è Riemann integrabile su $Q$. In altre parole,$$ f \text{ continua su } Q \Rightarrow f \in \mathcal{R} (Q)$$
Questa proposizione ricalca totalmente il caso di una funzione reale di una variabile reale.
Ma non sempre siamo così fortunati: a volte le funzioni presentano delle discontinuità, pur rimanendo limitate. L’analogo monodimensionale è una discontinuità di prima specie. In questo caso, la funzione, pur non essendo continua, rimane integrabile: quel che succede è che la discontinuità (un punto) è “troppo piccola” per influire sul comportamento (limitato) della funzione su tutto il suo dominio (che è uno o più intervalli). Anche nel caso bidimensionale possiamo trattare questi casi: abbiamo il concetto di funzione limitata, ma ci manca la capacità di distinguere quando un insieme è “troppo piccolo”. Occorre introdurre il concetto degli insiemi di misura nulla.
Un sottoinsieme limitato di $\mathbb{R}^2$ ha misura nulla se possiamo racchiuderlo dentro dei rettangoli piccoli a piacere. Più rigorosamente, sia $Z \subset \mathbb{R}^2$ un insieme limitato del piano. Diciamo che $Z$ ha misura nulla (in $\mathbb{R}^2$) se, per definizione, comunque preso $\varepsilon > 0$ esistono dei rettangoli $Q_1, Q_2, \dots, Q_N$ tali che:
- $Z$ è contenuto dentro i rettangoli: $Z \subset \bigcup_{i = 1}^N Q_i$.
- I rettangoli complessivamente non ricoprono un’area più grande di $\varepsilon$: $\sum_{i=1}^N | Q_i | < \varepsilon$.
Esempi di insiemi di misura nulla nel piano sono:
- Una collezione finita di punti $P_1, \dots, P_M$. Difatti, possiamo pensare di mettere ciascun punto $P_k$ al centro di un quadrato di lato piccolo a piacere.
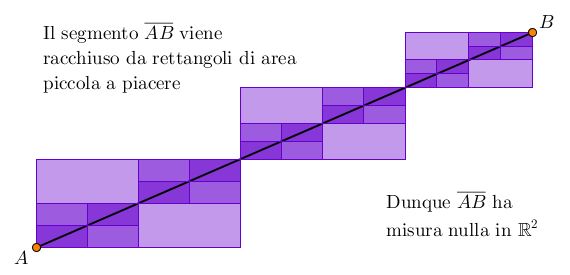
- Un segmento qualsiasi: la figura seguente illustra come si può dimostrare che il segmento $\overline{AB}$ ha misura nulla.
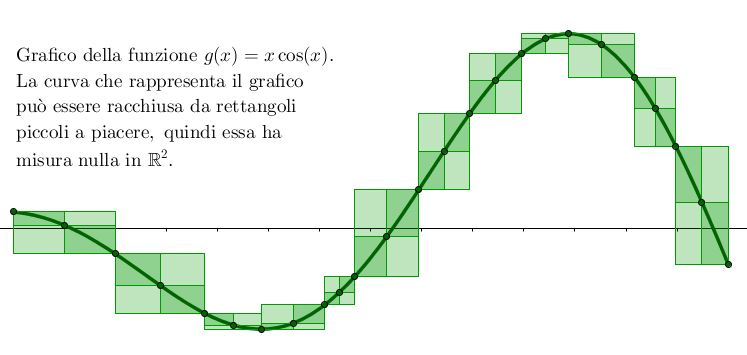
- Il grafico di una funzione $g: \mathbb{R} \longrightarrow \mathbb{R}$ opportunamente regolare. Anche in questo caso il grafico può essere racchiuso in rettangoli piccoli a piacere, come mostrato dalla seguente figura:
- In generale, una curva parametrizzata rettificabile in $\mathbb{R}^2$ ha misura nulla in $\mathbb{R}^2$.
Consideriamo ora una funzione $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$, ed un rettangolo $Q \subset \mathbb{R}^2$. $f$ si dice generalemente continua su $Q$ se l’insieme dei punti di discontinuità di $f$ ristretta all’insieme $Q$ ha misura nulla in $\mathbb{R}^2$.
Allora abbiamo una condizione un po’ più generale per controllare se una funzione sia Riemann integrabile:
Sia $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione limitata su un dominio rettangolare $Q$. Se $f$ è generalmente continua su $Q$, allora $f$ è Riemann integrabile su $Q$.
Ad esempio, consideriamo il rettangolo $Q = [0,1] \times [0,3]$, e definiamo per $(x,y) \in Q$ la funzione$$ f (x,y) = \begin{cases} \cos(x)\sin(y) + \frac{1}{5} & \text{ se } y \leq x^2 \\ x^2 + \frac{1}{3}y^2 + \frac{1}{5} & \text{ se } y > x^2 \end{cases}$$I due “tratti” della funzione $f$ sono, di per sé, delle funzioni continue; tuttavia, come viene illustrato nella figura seguente, si “incollano male” lungo la parabola $y = x^2$. Quindi l’insieme dei punti di discontinuità di $f$ all’interno del rettangolo $Q$ è rappresentato dalla parabola $y= x^2$, la quale però è a sua volta (nel piano) il grafico della funzione $g(x) = x^2$, che abbiamo detto avere misura nulla.
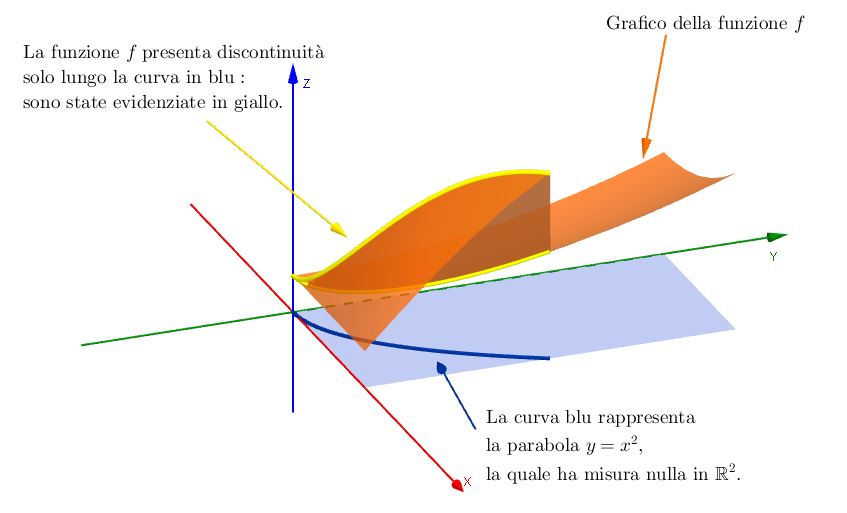
Concludiamo che $f$ è generalemente continua su $Q$, e dunque ivi integrabile.
Riemann in due variabili: Dominio Limitato
La condizione sulla forma del dominio che abbiamo imposto sino ad ora è una grande limitazione: in generale, infatti, ci sarà richiesto di calcolare l’integrale di una funzione su insiemi dalla forma più disparata.
Consideriamo allora un sottoinsieme $\Omega$ di $\mathbb{R}^2$. Vorremmo dare un senso all’integrale $\iint_{\Omega} f(x,y) dx \ dy$. Naturalmente, ci restrigiamo al caso in cui $\Omega$ sia limitato: come prima, si ricadrebbe nel caso di integrali indefiniti, che vogliamo evitare.
Se $\Omega$ è limitato, questo vuol dire che possiamo racchiuderlo in un rettangolo $Q$. Per definire l’integrale di $f$ su $\Omega$, allora, usiamo questo stratagemma: definiamo una funzione ausiliaria $\widetilde{f}$ come$$ \widetilde{f} (x,y) = \begin{cases} f(x,y) & \text{ se }(x,y) \in \Omega \\ 0 & \text{ se }(x,y) \in Q \setminus \Omega\end{cases}$$Siccome l’integrale rappresenta il volume sotteso al grafico della funzione, estendere $f$ al valore $0$, su un qualsiasi rettangolo $Q$, non avrà influenza sul valore dell’integrale: ma teoricamente la differenza è molto grande, poichè abbiamo definito l’integrale su un dominio rettangolare, mentre altrove l’orizzonte è ancora inesplorato.

Diciamo allora che la funzione $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$, definita sull’insieme limitato $ \Omega \subset \mathbb{R}^2 $, è Riemann integrabile su $\Omega$, e scriviamo $f \in \mathcal{R}(\Omega)$, se, preso $Q$ un rettangolo con $\Omega \subset Q$ e definita $\widetilde{f}$ come sopra, $\widetilde{f}$ è Riemann integrabile su $Q$. In tal caso, poniamo $$\iint_{\Omega} f (x,y) dx \ dy = \iint_Q \widetilde{f} (x,y) dx \ dy$$
La forma di $\Omega$ è cruciale per la determinazione dell’integrale. Una condizione che si può facilmente dedurre dalla definizione e dalle proposizioni precedenti è la seguente:
Sia $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione limitata definita su un insieme limitato $\Omega$. Se $f$ è generalmente continua su $\Omega$ e la sua frontiera $\partial \Omega$ ha misura nulla in $\mathbb{R}^2$, allora $f$ è Riemann integrabile su $\Omega$.
Questa proposizione deriva dal fatto che, qualora $\widetilde{f}$ fosse generalmente continua sul rettangolo $Q$, $\widetilde{f}$ sarebbe Riemann integrabile (per la proposizione precedente questa), e di conseguenza anche $f$ lo sarebbe su $\Omega$ (per definizione). Le eventuali discontinuità di $\widetilde{f}$ sono all’interno di $\Omega$ (dove però le controlliamo con $f$, che è generalmente continua per ipotesi) e sulla frontiera di $\Omega$, dove $f$ si raccorda al valore costante $0$. Ma se, a sua volta, $\partial \Omega$ ha misura nulla, siamo sicuri che $\widetilde{f}$ è generalmente continua su $Q$.
Presentiamo infine un utile corollario:
Siano $\Omega \subset \mathbb{R}^2$ un insieme limitato dalla frontiera di misura nulla, $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione definita e limitata su $\Omega$, e continua su tutti i punti interni di $\Omega$. Allora $f$ è Riemann integrabile su $\Omega$.
Tecniche di calcolo in $\mathbb{R}^2$
Quindi come si calcolano gli integrali?
Fino ad ora abbiamo parlato dell’integrale di Riemann un po’ troppo da lontano: sappiamo (a volte) dire quando una funzione è integrabile, ma non abbiamo ancora un modo per calcolare il valore effettivo dell’integrale.
Se sino ad ora l’integrale monodimensionale e quello bidimensionale avevano molte analogie, ora iniziano le differenze: per il calcolo integrale in una sola dimensione abbiamo a disposizione il teorema fondamentale del calcolo integrale; per gli integrali di funzioni di più variabili reali, no.
Forniremo qui di seguito una serie di tecniche per calcolare integrali doppi, in situazioni che, per quanto particolari, sono le più comuni.
Calcoli in $\mathbb{R}^2$: Domini Rettangolari
Se la funzione $f$ è limitata e definita su un rettangolo $Q$, possiamo pensare di “tagliare” il grafico, in direzione “orizzontale” o “verticale”, ottenendo una “fetta”, che poi facciamo scorrere nell’altra direzione, per ottenere il volume sotteso al grafico di $f$. Nell’illustrazione seguente, il grafico della funzione $f$ viene tagliato in direzione “orizzontale” da un piano:

Ma per potere “affettare” il grafico di $f$, dobbiamo garantire che la “fetta” abbia senso di esistere. Sia $Q = [a,b] \times [c,d]$. Quel che matematicamente richiediamo è che, per ogni scelta di $\overline{y} \in [c,d]$, la funzione $f(\, \overline{y} ): \mathbb{R} \longrightarrow \mathbb{R}$ (reale di una variabile reale), che ad ogni $x \in [a,b]$ associa $f(x,\overline{y})$, sia integrabile, nel senso del normale integrale, sull’intervallo $[c,d]$. Allora, in questo caso, possiamo garantire che la quantità $\int_a^b f(x,y) dx$, dipendente da $y$, è una funzione integrabile sull’intervallo $[c,d]$, e possiamo calcolare l’integrale doppio di $f$ su $Q$ come prima un integrale in $x$, e poi un integrale in $y$: $$ \iint_Q f (x,y) dx \ dy = \int_c^d \left( \int_a^b f(x,y) dx \right) dy$$In maniera del tutto analoga, possiamo pensare di “tagliare” prima in direzione verticale e dopo in orizzontale: invertendo il ruolo di $x$ ed $y$, richiediamo che $\forall \overline{x} \in [a,b]$ la funzione $f(\overline{x}, \ ): \mathbb{R} \longrightarrow \mathbb{R}$, che ad ogni $y \in [c,d]$ associa il valore $f(\overline{x}, y)$, sia integrabile su $[c,d]$; in tal caso, possiamo calcolare l’integrale doppio di $f$ su $Q$ in questo modo:$$ \iint_{Q} f(x , y) dx \ dy = \int_a^b \left( \int_c^d f(x, y) dy \right) dx$$
Anche se tecnicamente può risultare complicato, quel che stiamo in pratica effettuando è un integrale prima in $x$ e poi in $y$, o viceversa prima in $y$ e poi in $x$: la variabile ripspetto alla quale non stiamo integrando viene considerata una costante. Un esempio chiarirà subito la situazione.
Sia $Q = [0,1] \times [0,1]$, e definiamo $f$ a “tratti”, nel seguente modo: $$ f(x,y) = \begin{cases} 2xy & \text{se } y<x \\ x^3+2x^2y & \text{se } y \geq x\end{cases}$$Notiamo che la funzione è generalmente continua sul quadrato $Q$ (il suo insieme di discontinuità è un segmento), e dunque ivi Riemann integrabile.

Vogliamo calcolare quindi $\iint_Q f(x,y) \ dx dy$. Fissiamo $\overline{x}\in [0,1]$ e guardiamo chi è $f(\overline{x}, \ )$: è la funzione, della variabile $y$, definita a tratti$$ f(\overline{x}, y ) = f(x,y) = \begin{cases} 2 \overline{x} y & \text{se } y<\overline{x} \\ \overline{x}^3+2\overline{x}^2y & \text{se } y \geq \overline{x} \end{cases}$$Questa è una funzione che ha, al massimo, un punto di discontinuità, ed è quindi integrabile (nel senso dell’usuale integrale di funzione reale di una variabile reale) su $[0,1]$. Possiamo quindi calcolare l’integrale doppio di $f$ sul quadrato $Q$ prima integrando in $y$, e poi integrando in $x$: eseguiamo i calcoli##KATEX##\begin{aligned} \iint_Q f(x,y) \ dx dy & = \int_0^1\left( \int_0^1 f(x,y) \ dy \right) \ dx = \\ & = \int_0^1 \left( \int_0^x 2xy \ dy + \int_x^1 x^3+2x^2y \ dy \right) \ dx = \\ & = \int_0^1 \left(\left[ xy^2 \right]_{y=0}^{y=x} + \left[yx^3 +x^2y^2 \right]_{y=x}^{y=1} \right) \ dx = \\ & = \int_0^1 x^3 - 0 + x^3 + x^2 - (x^4 + x^4) \ dx = \\ & = \int_0^1 -2x^4 +2x^3 +x^2 \ dx = \\ & = \left[ -\frac{2}{5}x^4 + \frac{1}{2}x^4 + \frac{1}{3}x^3 \right]_{x=0}^{x=1} = \frac{1}{2} + \frac{1}{3} - \frac{2}{5} = \frac{13}{30} \end{aligned}##KATEX##
Calcoli in $\mathbb{R}^2$: Domini Semplici
Il passo successivo consiste nel considerare un insieme $\Omega$ “quasi” rettangolare. Definiamo un insieme limitato $\Omega \subset \mathbb{R}^2$ semplice rispetto all’asse $y$ se possiamo scriverlo come$$ \Omega = \left\{ (x,y) \in \mathbb{R}^2 \ \lvert \ a \leq x \leq b, g(x) \leq y \leq h(x) \right\}$$ove $g, h: \mathbb{R} \longrightarrow \mathbb{R}$ sono funzioni continue e definite sull’intervallo $[a,b]$.
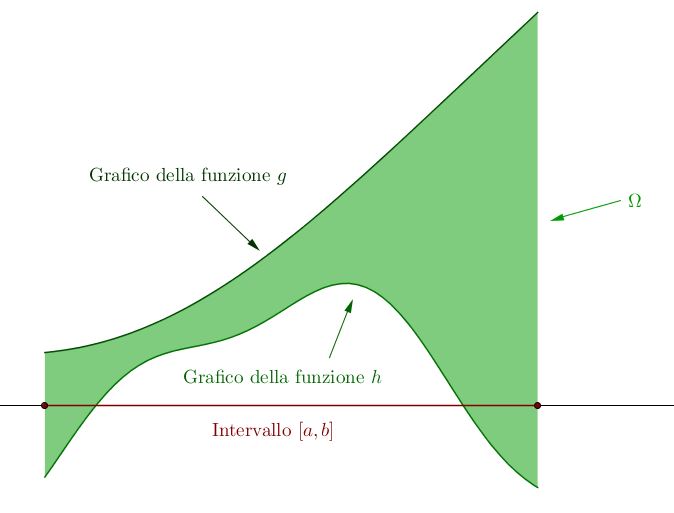
In modo simile, si definisce $\Omega$ semplice rispetto all’asse $x$ se$$ \Omega = \left\{ (x,y) \in \mathbb{R}^2 \ \lvert \ c \leq y \leq d, v(y) \leq x \leq w(y) \right\}$$ove $v, w: \mathbb{R} \longrightarrow \mathbb{R}$ sono funzioni continue e definite sull’intervallo $[c,d]$.
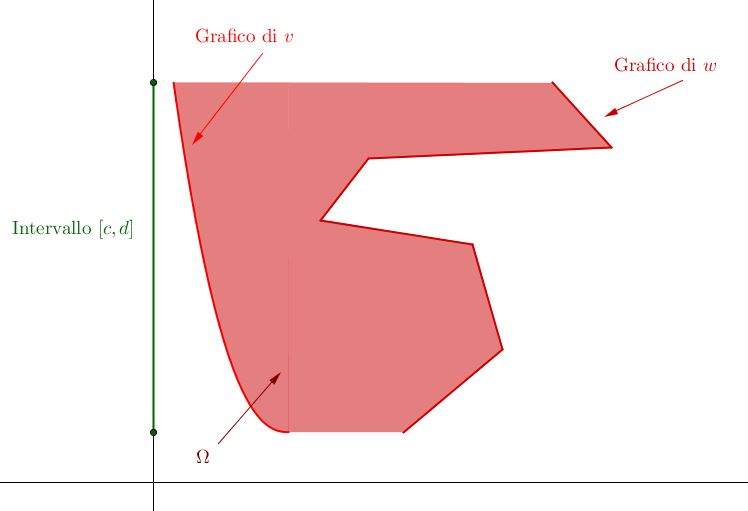
Sia a questo punto $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione definita e continua su $\Omega$ (attenzione che è una richiesta fondamentale!). Se $\Omega$ è un dominio semplice rispetto all’asse $y$, possiamo calcolare l’integrale doppio di $f$ su $\Omega$ come$$ \iint_\Omega f(x,y) dx \ dy = \int_a^b \left( \int_{g(x)}^{h(x)} f(x,y) dy \right) dx $$Se invece $\Omega$ è semplice rispetto all’asse $x$, abbiamo$$ \iint_\Omega f(x,y) dx \ dy = \int_c^d \left( \int_{v(y)}^{w(y)} f(x,y) dx \right) dy $$
Proprietà dell’integrale in $\mathbb{R}^2$
L’integrale doppio di Riemann, definito come nei paragrafi precedenti, gode di svariate proprietà che possono essere molto utili per effettuare i calcoli nella pratica. In particolare:
- L’integrale di Riemann è un funzionale lineare. Questo significa che, prese due funzioni $f, g\in \mathcal{R}(\Omega)$ e due numeri reali $\alpha, \beta$, vale la seguente uguaglianza:$$ \iint_{\Omega} \left( \alpha f(x,y) + \beta g(x,y) \right) dx \ dy = \alpha \iint_{\Omega} f(x,y) dx \ dy + \beta \iint_{\Omega} g(x,y) dx \ dy $$
- L’integrale di Riemann è un funzionale monotono. Questo significa che, prese due funzioni $f, g\in \mathcal{R}(\Omega)$ tali che $f \leq g$, si ha $$ \iint_{\Omega} f(x,y) dx \ dy \leq \iint_{\Omega} g(x,y) dx \ dy $$
- Se un insieme $\Omega$ si può spezzare in sottoinsiemi $\Omega_{k}$ che si intersecano in un insieme di misura nulla (cioè se $\displaystyle{\bigcap_k \Omega_k}$ ha misura nulla), l’integrale complessivo su tutto $\Omega$ si può calcolare come somma dei singoli integrali sui vari $\Omega_k$:$$ \iint_{\Omega} f(x,y) dx \ dy = \sum_k \iint_{\Omega_k} f(x,y) dx \ dy$$
Calcoli in $\mathbb{R}^2$: Cambio di coordinate
A volte è necessario vedere le cose sotto un altro aspetto, da un altro punto di vista. Per fare questo, in matematica, cambiamo coordinate: certe funzioni, descritte con opportune coordinate, risultano avere una forma molto più semplice, esteticamente più appetibile o, in certi casi, acquistano una descrizione in coordinate che prima non avevano nemmeno.
Il cambio di coordinate, però, viene avvertito dall’integrale: in effetti, l’integrale è una misura, e cambiare coordinate è un po’ come cambiare unità di misura. Abbiamo bisogno di un metodo di conversione.
Precisamente, un cambiamento di coordinate da $\mathbb{R}^2$ a $\mathbb{R}^2$ è una funzione $\Phi$ che alle “vecchie” coordinate ne sostituisce di nuove. Per essere un efficace cambiamento di coordinate, $\Phi$ deve essere una funzione continua, differenziabile, invertibile e con inversa $\Phi^{-1}$ a sua volta differenziabile. Nella pratica richiediamo che la sua matrice Jacobiana $J \Phi$ sia invertibile, ossia che abbia determinante diverso da $0$. In generale, un cambiamento di coordinate non sarà globale, ma avrà delle limitazioni.
Proposizione
Siano $\Omega$ un sottoinsieme limitato di $\mathbb{R}^2$, la cui frontiera $\partial \Omega$ abbia misura nulla, ed $f: \mathbb{R}^2 \longrightarrow \mathbb{R}$ una funzione Riemann integrabile su $\Omega$. Sia inoltre $\Phi$ un cambiamento di coordinate su $\mathbb{R}^2$, che dalle coordinate $(u,v)$ passa a $(x,y) = \Phi \left ( (u,v) \right)$. Allora $f \circ \Phi$, ossia la funzione $f$ descritta nelle coordinate $(u,v)$, è Riemann integrabile su $\Phi^{-1} ( \Omega )$, e vale$$ \iint_{\Omega} f(x,y) dx \ dy = \iint_{\Phi^{-1} (\Omega) } (f \circ \Phi) (u,v) | \det (J \Phi) | du \ dv$$
Anche in questo caso un esempio aiuta a risolvere eventuali dubbi. Volgiamo integrare la funzione $f(x,y) = x^2 - y^2$ sull’insieme $\Omega = \left \{ (x,y) \in \mathbb{R}^2 \ \lvert \ 0 \leq x+y \leq 1, 0 \leq x-y \leq 1 \right \}$. La descrizione stessa di $\Omega$, come spesso succede, suggerisce il cambio di variabili $$ \begin{cases} x+y = u \\ x-y = v\end{cases}$$Questa descrive $(u,v)$ in funzione di $(x,y)$: si tratta quindi di $\Phi^{-1}$, non di $\Phi$. La matrice jacobiana di questa trasformazione è $$J (\Phi^{-1}) = \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right)$$Questa matrice ha determinante $-2$, quindi $J \Phi $ ha determinante $\frac{1}{-2} = -\frac{1}{2}$. Descriviamo ora $f$ ed $\Omega$ nelle nuove coordinate $u,v$: per quanto riguarda $f$, siccome $f (x,y) = x^2 - y^2 = (x+y)(x-y) $, abbiamo $f \circ \Phi (x,y) = f (u,v) = u \ v$; per quanto riguarda $\Omega$, questo diviene semplicemente il quadrato $[0,1] \times [0,1]$. Ora siamo pronti per calcolare l’integrale desiderato:##KATEX##\begin{aligned} \iint_{\Omega} f(x,y) \ dx dy & = \iint_{[0,1] \times [0,1]} f(u,v) | \det (J \Phi)| \ du dv = \\ & = \frac{1}{2} \iint_{[0,1] \times [0,1]} u v \ du dv = \\ & = \frac{1}{2} \int_0^1 \left( \int_0^1 u v du \right) dv = \frac{1}{2} \int_0^1 \frac{1}{2} \left[ u^2 v \right]_{u=0}^{u=1} dv = \\ & = \frac{1}{4} \int_0^1 v dv = \frac{1}{8} \end{aligned}##KATEX##
Un caso molto particolare sono le coordinate polari in $\mathbb{R}^2$. Il cambiamento di coordinate che utilizziamo è il seguente:$$ \Phi (r,\theta) = \begin{cases} x (r, \theta) = r \cos (\theta) \\ y(r,\theta) = r \sin (\theta) \end{cases}$$In questo caso, abbiamo che il determinante dello jacobiano vale esattamente $r$.
Integrale di Riemann di funzioni reali di tre variabili reali
Il caso delle funzioni reali di due variabili reali può essere facilmente generalizzato a funzioni $f: \mathbb{R}^n \longrightarrow \mathbb{R}$. Il livello di astrazione tuttavia cresce sempre di più: già incrementando la dimensione di $1$, cioè parlando di funzioni reali di tre variabili reali, il grafico di tali funzioni sarebbe situato in $\mathbb{R}^4$, che, ahimé, non possiamo nemmeno rappresentare!
Tali funzioni, tuttavia, sono l’ultimo gradino prima di un livello completamente astratto: in questo caso, infatti, almeno l’insieme su cui $f$ viene integrata possiamo visualizzarlo: si tratta di un sottoinsieme di $\mathbb{R}^3$, quindi (in generale) è rappresentato da un volume. Per quanto riguarda il significato dell’integrale di Riemann, possiamo pensare ad $f$, prendendo spunto dalla fisica, come ad una densità, ossia un numero, un valore, appiccicato a ciascun punto dello spazio: calcolare l’integrale di Riemann di $f$ su di un sottoinsieme $\Omega$ di $\mathbb{R}^3$ sarà dunque come calcolare la massa racchiusa in nel volume occupato da $\Omega$, se la distribuzione della massa è data dalla “densità” $f$.
L’astrazione ha i suoi vantaggi, però: infatti tutti i risultati che abbiamo elencato per gli integrali di funzioni reali di due variabili reali si possono generalizzare al caso di tre variabili reali semplicemente aggiungendo la terza coordinata, $z$. Ovviamente le tecniche di calcolo andranno modificate.
In particolare, i rettangoli $Q$ verranno sostituiti da parallelepipedi retti, che chiameremo sempre $Q$ con lati paralleli agli assi cartesiani.
Elenchiamo i risultati di validità generale, i quali, per l’appunto, valgono anche per funzioni $f: \mathbb{R}^3 \longrightarrow \mathbb{R}$.
- Una funzione $f$, limitata e definita sul un parallelepipedo $Q$, è per definizione Riemann integrabile su $Q$ se $$ \text{sup}_{\mathcal{P}} \left( s(f, \mathcal{P}) \right) = \text{inf}_{\mathcal{P}} \left( S(f, \mathcal{P}) \right) $$dove le somme inferiori e le somme superiori sono calcolate a partire da partizioni (tridimensionali) del parallelepipedo $Q$. Questo numero viene detto l’integrale (triplo) di $f$ su $Q$ e viene indicato dal simbolo$$ \iiint_{Q} f(x,y,z) dx \ dy \ dz $$Se una funzione è Riemann integrabile su $Q$, si scrive anche $f \in \mathcal{R} (Q)$.
- Funzioni continue su parallelepipedi sono ivi Riemann integrabili.
- Un sottoinsieme di $\mathbb{R}^3$ si definisce di misura nulla in maniera del tutto analoga a quanto fatto in due dimensioni: bisogna prestare attenzione, tuttavia, dato che dobbiamo “inscatolare” un insieme all’interno di parallelepipedi. In particolare, le superfici (con un minimo di regolarità) sono insiemi di misura nulla in $\mathbb{R}^3$.
- Una funzione $f$ si dice generalmente continua su un parallelepipedo $Q$ se l’insieme dei punti di $Q$ in cui non è continua ha misura nulla in $\mathbb{R}^3$.
- Funzioni generalmente continue su parallelepipedi sono ivi Riemann integrabili.
- Se, al posto di avere un parallelepipedo abbiamo a disposizione un volume limitato $\Omega \subset \mathbb{R}^3$, usiamo lo stesso stratagemma che abbiamo usato in due dimensioni: data $f: \Omega \longrightarrow \mathbb{R}$, prendiamo un parallelepipedo $Q$ che racchiuda $\Omega$, e definiamo su $Q$ una nuova funzione $\widetilde{f}$ nel seguente modo$$ \widetilde{f} (x,y,z) = \begin{cases} f(x,y,z) & \text{ se }(x,y,z) \in \Omega \\ 0 & \text{ se }(x,y,z) \in Q \setminus \Omega\end{cases}$$
- Analogamente a quanto succede in due dimensioni, abbiamo che una funzione $f$, definita, limitata e generalmente continua su un insieme limitato $\Omega$, il quale a sua volta ha frontiera $\partial \Omega$ di misura nulla in $\mathbb{R}^3$, è Riemann integrabile su $\Omega$. Come ipotesi più restrittiva, possiamo richiedere che $f$ sia continua anziché generalmente continua.
Proprietà dell’integrale in $\mathbb{R}^3$
Definito in questo modo, l’integrale triplo di Riemann gode delle stesse proprietà che aveva il suo collega in dimensione $2$:
- Si tratta di un funzionale lineare: comunque scelte due funzioni $f, g\in \mathcal{R}(\Omega)$ e due numeri reali $\alpha, \beta$, vale $$ \iiint_{\Omega} \left( \alpha f(x,y,z) + \beta g(x,y,z) \right) dx \ dy \ dz = \alpha \iiint_{\Omega} f(x,y,z) dx \ dy dz + \beta \iiint_{\Omega} g(x,y,z) dx \ dy \ dz $$
- È sempre un funzionale monotono: se $f$ e $g$ sono Riemann integrabili su $\Omega$ e $f \leq g$ ovunque in $\Omega$, vale lo stesso ordinamento per gli integrali tripli:$$ \iint_{\Omega} f(x,y,z) dx \ dy \ dz \leq \iint_{\Omega} g(x,y,z) dx \ dy \ dz$$
- Se un volume $\Omega$ si può spezzare in “volumetti” $\Omega_{k}$ che si intersecano in un insieme di misura nulla in $\mathbb{R}^3$, l’integrale complessivo su tutto $\Omega$ si può calcolare come somma dei singoli integrali sui vari $\Omega_k$:$$ \iiint_{\Omega} f(x,y,z) dx \ dy \ dz= \sum_k \iiint_{\Omega_k} f(x,y,z) dx \ dy \ dz$$
Tecniche di calcolo in $\mathbb{R}^3$
Sebbene l’aggiunta di una sola coordinata non costituisce un grosso scoglio, almeno dal punto di vista teorico, dal punto di vista pratico ci complica abbastanza le cose. Per questo si sfruttano alcuni stratagemmi, che andiamo di seguito ad illustrare.
Calcoli in $\mathbb{R}^3$: Integrali per Fili
Il primo caso particolare che andiamo ad analizzare è quello in cui il volume $\Omega$ su cui dobbiamo integrare la funzione $f$ può essere racchiuso da un “tetto” e da un “pavimento”: matematicamente richiediamo quanto segue.
Sia $\Omega$ un insieme limitato in $\mathbb{R}^3$. Si dice che $\Omega$ è normale rispetto all’asse $z$ se può essere descritto nel seguente modo:$$\Omega = \left\{ (x,y,z) \in \mathbb{R}^3 \ \lvert \ (x,y) \in D, \alpha(x,y) \leq z \leq \beta(x,y) \right\}$$ove $D$ è un insieme (di $\mathbb{R}^2$) limitato e la cui frontiera ha misura nulla (in $\mathbb{R}^2$), mentre $\alpha$ e $\beta$ sono opportune funzioni da $\mathbb{R}^2$ a $\mathbb{R}$, continue su $D$. Se $\Omega$ si può descrivere in questo modo, allora esso è effettivamente il volume racchiuso tra i grafici di $\alpha$ e $\beta$; l’idea è quindi di fissare un punto $(x,y) \in D$, e di integrare $f$ sul “filo” che otteniamo in questo modo tra i due grafici in questione, e successivamente di far variare $(x,y)$ all’interno di $D$. Una figura vale più di mille parole:

Consideriamo allora $f: \mathbb{R}^3 \longrightarrow \mathbb{R}$, definita, limitata e generalmente continua su $\Omega$. A questo punto, se $\Omega$ è normale rispetto all’asse $z$, possiamo calcolare l’integrale $\iiint_{\Omega} f(x,y,z) dx \ dy \ dz $ nel seguente modo:$$ \iiint_{\Omega} f(x,y,z) dx \ dy \ dz = \iint_D \left( \int_{\alpha(x,y)}^{\beta(x,y)} f(x,y,z) dz \right) dx \ dy$$Questo integrale prevede anche il calcolo di un integrale doppio, che si può calcolare con una qualunque delle tecniche acquisite in precedenza, a seconda di come è fatto $D$.
Come esempio, proviamo a calcolare $ \iiint_{\Omega} f(x,y,z ) \ dx dy dz $ dove $f(x,y,z) = xy e^z$ e $\Omega$ è descritto come $ \left \{ (x,y,z) \in \mathbb{R}^2 \ \lvert \ 0 \leq x \leq 1, -2 < y < 0, 0 \leq z <x^2 + y^2 \right \}$. Il ruolo dell’insieme $D$ è svolto dal rettangolo $I \times J = [0,1] \times [-2,0]$, mentre le due funzioni $\alpha$ e $\beta$ sono, rispettivamente, la funzione costante $z=0$ e la funzione $z=x^2 + y^2$. La figura seguente rappresenta $\Omega$:
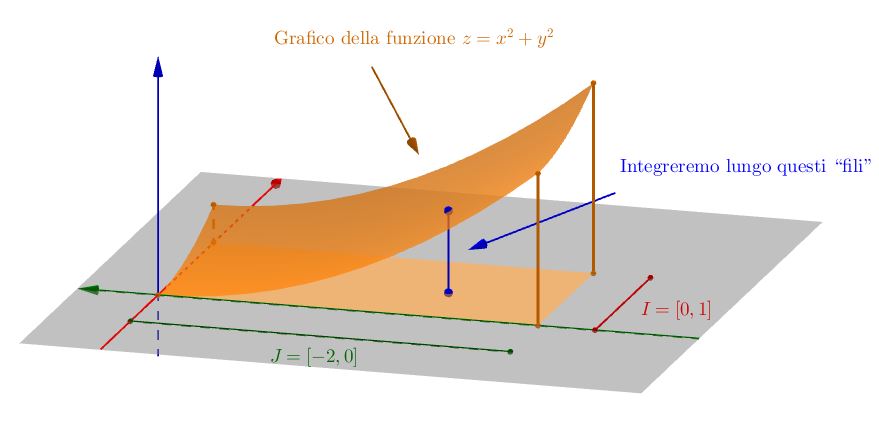
Come si vede, il $\Omega$ è limitato; inoltre, la sua frontiera è costituita dal rettangolo $I \times J$, dalla parte del grafico della funzione $\beta$ che sovrasta tale rettangolo (una superficie) e dalle quattro superfici laterali: tutti questi insiemi hanno misura nulla in $\mathbb{R}^3$, in quanto, appunto, superfici. Inoltre, $f$ è continua e limitata su $\Omega$.
Possiamo allora calcolare l'integrale richiesto nel seguente modo:##KATEX##\begin{aligned} \iiint_{\Omega} f(x,y,z) \ dx dy dz & = \iint_{D} \left( \int_0^{x^2+y^2} xy e^z \ dz \right) \ dx dy = \\ & = \iint_{D} xy \left( \int_0^{x^2 + y^2} e^z \ dz\right) \ dx dy = \\ & = \iint_{D} xy\left(e^{x^2 + y^2} -1 \right) = \\ & = \int_0^1 x e^{x^2} \ dx \int_{-2}^0 y e^{y^2} \ dy - \int_0^1 x \ dx \int_{-2}^0 y \ dy = \\ & = \frac{1}{4}\left( e-1\right) \left(1- e^{+4} \right) - \frac{1}{2}\frac{1}{2} \ 4 = \frac{e + e^4 - e^5 - 5}{4}.\end{aligned}##KATEX##
Calcoli in $\mathbb{R}^3$: Integrali per Strati
In questo caso assumiamo che $\Omega$ assuma una forma agevole da descrivere matematicamente se consideriamo le sue “sezioni” orizzontali: fissiamo una quota $\overline{z}$ e tagliamo $\Omega$ con il piano $z= \overline{z}$. Chiamiamo l’insieme che otteniamo $\Omega_{\overline{z}}$, ossia$$ \Omega_{\overline{z}} = \left\{ (x,y,z) \in \Omega \ \lvert \ z = \overline{z} \right\}$$Vogliamo che $\Omega$ si possa descrivere come stratificazione di questi $\Omega_{\overline{z}}$ e che essi si “comportino bene”: più precismanete, richiediamo che:
- Per ogni punto $(x,y,z) \in \Omega$, si abbia $z \in [a,b]$, per un opportuno intervallo $[a,b]$ chiuso e limitato.
- Per ogni $\overline{z} \in [a,b]$ l’insieme $\Omega_{\overline{z}}$ sia limitato e la sua frontiera abbia misura nulla in $\mathbb{R}^2$.

A questo punto, consideriamo $f: \mathbb{R}^3 \longrightarrow \mathbb{R}$, definita, limitata e generalmente continua su $\Omega$, con $\Omega$ dotato delle proprietà appena descritte. In questo caso possiamo calcolare l’intergale $\iiint_{\Omega} f(x,y,z) dx \ dy \ dz $ “per strati”, cioè prima ingerando $f$ su $\Omega_{\overline{z}}$, e poi facendo variare la quota $\overline{z} \in [a,b]$: matematicamente, vale infatti$$ \iiint_{\Omega} f(x,y,z) dx \ dy \ dz = \int_a^b \left( \iint_{\Omega_{z}} f(x,y,z) dx \ dy \right) dz $$Anche in questa formula è previsto il calcolo di un integrale doppio, per il quale dobbiamo escogitare qualche metodo specifico, a seconda della forma di $\Omega_{z}$.
Per fare un esempio, cerchiamo di calcolare il volume occupato del cilindro di altezza $h$ così descritto: $\Omega = \{ (x,y,z) \in \mathbb{R}^3 \ \lvert \ 0 \leq z \leq h, x^2 + y^2 \leq z \}$. Per ogni $z$ fissato nell’intervallo $[0,h]$, $\Omega_z$ è $\{(x,y) \in \mathbb{R}^2 \ \lvert \ x^2 + y^2 \leq z\}$, che altro non è che una circonferenza centrata nell’origine e di raggio $\sqrt{z}$, che ha area $\pi \sqrt{z}^2 = \pi z$. Possiamo quindi calcolare il volume richiesto come segue$$\iiint_{\Omega} \ dx dy dz = \int_0^h \left( \iint_{\Omega_z} \ dx dy \right) \ dz = \int_0^h \pi z dz = \pi \frac{h^2}{2}$$
Non è detto che un singolo insieme possa essere descritto unicamente per fili o per strati: ad esempio il tetraedro (irregolare) $\Omega = \{(x,y,z) \in \mathbb{R}^3 \ \lvert \ x \geq 0, y \geq 0, z \geq 0, x+y+z \leq 1\}$ può essere descritto per strati come per fili:
- Per strati abbiamo $z \in [0,1]$ e $\Omega_z = \{ (x,y) \in \mathbb{R}^2 \ \lvert \ x \geq 0, y \geq 0, x+z \leq 1-z \}$.
- Per fili abbiamo $D = \{ (x,y) \in \mathbb{R}^2 \ \lvert \ x \geq 0, y \geq 0, x+y \leq 1 \}$ e $\Omega = \{ (x,y,z) \in \mathbb{R}^3 \ \lvert \ (x,y) \in D, 0 \leq z \leq 1-x-y\}$.
La scelta dell’una o dell’altra forma dipende dal calcolo che occorre effetuare e, in ultima analisi, all’espressione della funzione integranda $f$.
Calcoli in $\mathbb{R}^3$: Cambiamento di Variabili
Più aumentano le variabili, più frequentemente occorre cambiarle. Per fortuna, quanto abbiamo descritto nel caso bidimensionale si applica a $\mathbb{R}^n$ con $n \geq 1$: sarà quindi sufficiente riadattare tutte le definizioni ad $\mathbb{R}^3$, e non occorrerà aggiungere altro.
Stiamo parlando di un cambiamento di coordinate $\Phi: \mathbb{R}^3 \longrightarrow \mathbb{R}^3$ che sostituisce tre coordinate $(u,v,w)$ con altre tre $(x,y,z)$, ove $\Phi$ è una funzione continua, differenziabile e invertibile su un particoalre insieme, e con inversa continua e differenziale: sotto queste ipotesi, il determinante della matrice jacobiana $\text{det}(J \Phi)$ è sempre diverso da zero. Sussiste la seguente proposizione:
Siano $\Omega$ un sottoinsieme limitato di $\mathbb{R}^3$, la cui frontiera $\partial \Omega$ abbia misura nulla in $\mathbb{R}^3$, ed $f: \mathbb{R}^3 \longrightarrow \mathbb{R}$ una funzione Riemann integrabile su $\Omega$. Sia inoltre $\Phi$ un cambiamento di coordinate su $\mathbb{R}^3$, che dalle coordinate $(u,v,w)$ passa a $(x,y,z) = \Phi \left ( (u,v,w) \right)$. Allora $f \circ \Phi$, ossia la funzione $f$ descritta nelle coordinate $(u,v,w)$, è Riemann integrabile su $\Phi^{-1} ( \Omega )$, e vale$$ \iiint_{\Omega} f(x,y,z) dx \ dy \ dz = \iiint_{\Phi^{-1} (\Omega) } (f \circ \Phi) (u,v,w) | \det (J \Phi) | du \ dv \ dw $$
Ricordiamo i cambiamenti di coordinate più comuni in $\mathbb{R}^3$, e i determinanti dei relativi jacobiani: per le coordinate cilindriche $(R,\Theta,z)$ abbiamo $| \det (J \Phi) | = R$; per le coordinate sferiche $(r,\theta, \phi)$ otteniamo invece $| \det (J \Phi) | = r^2 \sin(\phi)$.
Come ultimo esempio, cerchiamo di calcolare il volume dell’insieme $\Omega = \{ (x,y,z) \in \mathbb{R}^3 \ \lvert \ z+4 \geq \sqrt{ x^2 + y^2}, x^2 + y^2 + z^2 \geq 1 x^2 + y^2 \leq 4, z \leq 0 \}$. $\Omega$ risulta molto più agevole se descritto in coordinate cilindriche $(R,\Theta,z)$: abbiamo infatti $\Omega = \{(R,\Theta,z) \ \lvert \ \Theta \in (0, 2\pi], z \geq R - 4, R^2 + z^2 \geq 1, R^2 \leq 4, z \leq 0 \}$. Con un po’ di ingegnosità, possiamo riscrivere $\Omega$, sempre in coordinate cilindriche, nel seguente modo:$$\Omega = \left\{(R,\Theta,z) \ \lvert \ \Theta \in (0, 2\pi], R \in [0,1], R-4 \leq z \leq -\sqrt{1-R^2} \right\} \bigcup \left\{(R,\Theta,z) \ \lvert \ \Theta \in (0, 2\pi], R \in [1,2], R-4 \leq z \leq 0 \right\}$$Ora siamo pronti per calcolarne il volume:##KATEX##\begin{aligned} \iiint_{\Omega} dx dy dz & = \int_0^{2\pi} \left( \int_0^1 \left( \int_{R-4}^{-\sqrt{1-R^2}} R dz \right) dR \right)d\Theta + \int_0^{2\pi} \left( \int_1^2 \left( \int_{R-4}^0 R dz \right) dR \right) d\Theta = \\ & = 2 \pi \left( \int_0^1 R \int_{R-4}^{-\sqrt{1-R^2}} dz dR + \int_1^2 R \int_{R-4}^0 dz dR \right) = \\ & = 2 \pi \left( \int_0^1 -R \sqrt{1-R^2} - R( R -4) dR + \int_1^2 -R(R-4) dR \right) = \\ & = 2 \pi \left( \frac{1}{3} \left[ (1-R^2)^{\frac{3}{2}} \right]_0^1 - \frac{1}{3} + 2 - \left[ -\frac{1}{3}R^3 + 2R^2 \right]_1^2 \right) =\\ & = 2\pi \left( -\frac{1}{3} - \frac{1}{3} +2 -\frac{8}{3} + 8 +\frac{1}{3} -2 \right) = 10 \pi \end{aligned}##KATEX##