Per una funzione $g$ di una variabile reale, derivabile in un punto $x_0$, è possibile definire il suo differenziale in $x_0$. Intuitivamente il differenziale quantifica lo scarto tra la retta tangente a $g$ in $x_0$ e il grafico della funzione $g$ stessa, in dipendenza del variare infinitesimo delle ascisse (in prossimità di $x_0$). Si può inoltre dimostrare che una funzione è differenziabile (cioè, ammette differenziale) se e solo se è derivabile: in poche parole il concetto di derivabilità si “confonde” con quello di differenziabilità, quando lavoriamo con una variabile sola.
Quando consideriamo funzioni di più variabili, invece, la situazione si fa più complessa. Come vedremo in questa lezione, una funzione potrà ammettere gradiente (che è il concetto analogo a quello di derivata in più dimensioni) ma non essere differenziabile.
Definizione
Una funzione $f: \mathbb{R}^n \rightarrow \mathbb{R}$ si dice differenziabile in $P$ se esiste una applicazione lineare $L_f: \mathbb{R}^n \rightarrow \mathbb{R}$ tale che sia rispettata l’uguaglianza$$f(P+T)-f(P) = L_f(T) + \varepsilon(T)$$dove specifichiamo che:
- $T$ tende a $O$ (l’origine degli assi) e il punto chiamato $P+T$ è il punto ottenuto sommando le coordinate di $P$ e $T$;
- $\varepsilon$ è una qualsiasi funzione da $\mathbb{R}^n$ a $\mathbb{R}$ tale per cui valga il limite $$\lim_{T \to O} \frac{\varepsilon(T)}{d(T,O)}=0$$dove $d$ è la distanza euclidea in $\mathbb{R}^n$.
In maniera del tutto equivalente, diremo che $f$ è differenziabile in $P$ se possiamo trovare una applicazione lineare $L_f$ come sopra tale per cui valga il seguente limite: $$\lim_{T \to O} \frac{f(P+T) - f(P) - L_f(T)}{d(T,O)} = 0$$L’applicazione $L_f$ viene chiamata differenziale primo di $f$.
Una funzione differenziabile soddisfa automaticamente una serie di proprietà molto utili, a cui spesso ci si riferisce chiamandole condizioni necessarie per la differenziabilità. Elenchiamo alcune di quelle più importanti, senza dimostrarne la validità.
- Una funzione differenziabile è anche continua.
- Le derivate direzionali - e quindi il gradiente - di una funzione differenziabile esistono sempre.
- L’applicazione $L_f$, che sappiamo esistere per la definizione di differenziabilità in un punto $P$, è in realtà la seguente: ##KATEX##\begin{aligned}L_f: \mathbb{R}^n & \rightarrow \mathbb{R} \\ T & \mapsto \nabla f(P) \cdot \vec{OT} \end{aligned}##KATEX##dove $\cdot$ è il prodotto scalare e $\vec{OT}$ è il vettore che collega l’origine degli assi con $T$.
- Una funzione differenziabile soddisfa la formula del gradiente, che permette di calcolare il valore di una qualsiasi derivata direzionale a partire dalle sole derivate parziali.
Vale anche il seguente fondamentale teorema.
TEOREMA (del differenziale totale). Consideriamo una funzione $f: \mathbb{R}^n \rightarrow \mathbb{R}$ con derivate parziali continue in un certo punto $P \in \mathbb{R}^n$. Allora $f$ è differenziabile in $P$.
È importante fare le seguenti considerazioni relativamente ai risultati elencati poco fa.
- Una funzione continua non è necessariamente differenziabile. Per esempio, anche solo rimanendo nell’ambito delle funzioni di una variabile, qualsiasi funzione con un punto angoloso è continua ma non derivabile (e quindi non differenziabile) in quel punto.
- L’esistenza di tutte le derivate direzionali in un punto non garantisce la differenziabilità di una funzione in quel punto. Per esempio, è possibile dimostrare che la funzione $$f(x, y) = \begin{cases} \left ( \frac{y}{x^2} \left (1 - \frac{y}{x^2} \right ) \right)^2 & \quad \text{se }y \leq 0 \ \vee \ y \geq x^2 \\ 0 & \quad \text{se }0 < y < x^2 \end{cases}$$ammette tutte le derivate direzionali nell’origine $O$, ma che non è continua in $O$ (e quindi non è differenziabile).
- Una funzione differenziabile non ha necessariamente derivate parziali continue (ovvero, il teorema del differenziale totale funziona solo in un verso). Per esempio, la funzione $$f(x, y)= \begin{cases} (x^2+y^2) \sin \left ( \frac{1}{\sqrt{x^2+y^2}} \right ) & \quad \text{se }(x, y) \neq (0,0) \\ 0 & \quad \text{se }(x, y) = (0,0) \end{cases}$$è differenziabile nell’origine, ma le derivate parziali di $f$ in $O$ non sono continue.
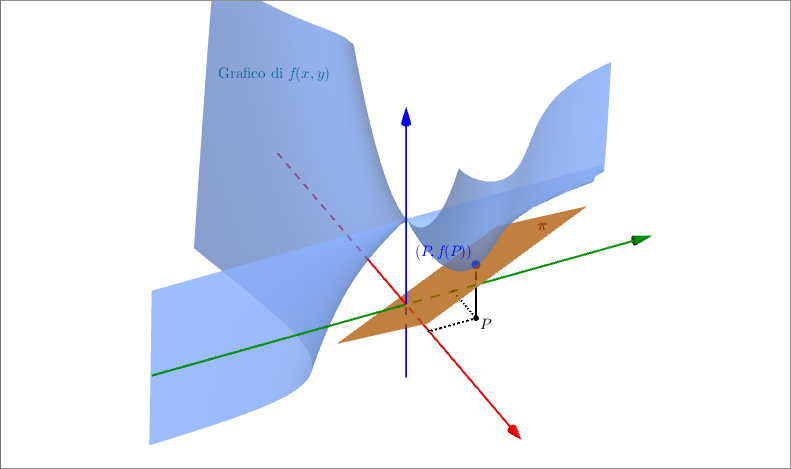
Piano tangente al grafico di una funzione di due variabili
Così come la differenziabilità (cioè, la derivabilità) di una funzione di una variabile ci permette di ricavare l’equazione della retta tangente al suo grafico, la differenziabilità di una funzione di due variabili ci permette di costruire il piano tangente al grafico della funzione.
Definizione
Prendiamo una funzione $f: \mathbb{R}^2 \rightarrow \mathbb{R}$ differenziabile in un punto $P \in \mathbb{R}^2$. Il sottoinsieme di $\mathbb{R}^3$ definito dall’equazione $$\pi: \quad z = f(P)+L_f(x,y) - L_f(P)$$è detto piano tangente al grafico di $f$ nel punto $(P, f(P))$.
Facciamo un esempio per capire come determinare concretamente l’equazione di un piano tangente.
Consideriamo la funzione $$f(x, y) = x^2 + 3xy^2-2\sqrt{xy} + 1$$e determiniamo il piano tangente alla funzione nel punto $P \equiv \left ( \frac{1}{2}, \frac{1}{2} \right )$. Per prima cosa calcoliamo le derivate parziali di $f$: ##KATEX##\begin{aligned} \frac{\partial f}{\partial x} & = 2x + 3y^2 - \frac{y}{\sqrt{xy}} \\ \frac{\partial f}{\partial y} & = 6xy - \frac{x}{\sqrt{xy}} \end{aligned}##KATEX##Si vede che esse sono continue in $P$, e quindi per il teorema del differenziale totale possiamo dire che $f$ è differenziabile in $P$. L’applicazione $L_f$, in $P$, associa a un punto $A \in \mathbb{R}^2$ il prodotto scalare tra il gradiente di $f$ in $P$ e il vettore che ha per componenti le coordinate del punto $A$. Dato che $$\nabla f (P) = \left ( \frac{\partial f}{\partial x}(P), \frac{\partial f}{\partial y} (P) \right ) = \left ( \frac{3}{4}, \frac{1}{2} \right )$$allora possiamo dire che ##KATEX##\begin{aligned}L_f : \mathbb{R}^2 & \rightarrow \mathbb{R} \\ (x,y) & \mapsto \frac{3}{4}x + \frac{1}{2}y \end{aligned}##KATEX##L’equazione del piano $\pi$ tangente al grafico di $f$ nel punto $P$ avrà quindi la seguente equazione: ##KATEX##\begin{aligned} z & = f(P) +L_f(x,y) - L_f(P) \quad \Rightarrow \\ \Rightarrow \quad z & = \frac{5}{8} + \left ( \frac{3}{4}x + \frac{1}{2}y \right ) - \left ( \frac{3}{4}\cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} \right ) \quad \Rightarrow \\ \Rightarrow \quad z & = \frac{3}{4}x + \frac{1}{2}y \end{aligned}##KATEX##Ecco il grafico di $f$ - che essendo definita solo nel primo e nel terzo quadrante non ha grafico definito per tutto $\mathbb{R}^2$ - rappresentato insieme al piano $\pi$.