La definizione di limite per una funzione di più variabili, come abbiamo visto, presenta alcune problematiche legate alla direzione lungo la quale ci si avvicina al punto per il quale vogliamo calcolare il limite. Il concetto di direzione è centrale anche quando vogliamo iniziare a studiare qualcosa di analogo alle derivate, per le funzioni di più variabili.
Definizione
Consideriamo una funzione di più variabili $f: \mathbb{R}^n \rightarrow \mathbb{R}$ e un punto $V \equiv (v_1, v_2, \ldots, v_n)$ di $\mathbb{R}^n$; il punto $V$ determina il vettore $\overrightarrow{OV}$ che denoteremo con $v$. Prendiamo anche un punto $X \equiv (x_1, x_2, \ldots, x_n)$ nel dominio di $f$.
Chiamiamo derivata direzionale di $f$ in $X$ lungo la direzione $v$ il seguente limite: $$\lim_{h \to 0} \frac{f(x_1 + hv_1,x_2 + hv_2, \ \ldots \ , x_n + hv_n) - f(x_1, x_2, \ldots, x_n)}{h}$$
La notazione che utilizzeremo per indicare la derivata direzionale di $f$ sarà, in genere, la seguente: $$\frac{\partial f}{\partial v}\left ( X \right )$$Altre notazioni in uso sono le seguenti: $$D_vf(X), \quad \frac{\partial f}{\partial v}, \quad D_vf$$In particolare, le ultime due si utilizzano quando non è necessario specificare (o è sottointeso) il punto $X$ in cui stiamo derivando.
Definizione
La derivata direzionale di una funzione $f: \mathbb{R}^n \rightarrow \mathbb{R}$, calcolata lungo la direzione $w$ individuata da un punto $W$ su un asse cartesiano, si dice derivata parziale.
Se $W$ sta su un certo asse $x_i$ di $\mathbb{R}^n$, con $1 \leq i \leq n$, esso avrà coordinate $$W \equiv ( 0, 0, \ldots, w_i, \ldots , 0) \quad \text{con }w_i\text{ alla posizione }i$$e utilizzeremo la seguente notazione: $$\frac{\partial f}{\partial x_i}(P) := \frac{\partial f}{\partial w}(P) = \lim_{h \to 0} \frac{f(p_1,p_2, \ \ldots \ , p_i + hw_i, \ \ldots \ , p_n) - f(p_1, p_2, \ldots, p_n)}{h}$$
Prima di analizzare qualche esempio - che sicuramente potrà aiutarci a capire meglio le definizioni appena date - facciamo alcune considerazioni.
- È importante notare che i limiti in questione sono svolti rispetto alla variabile $h \in \mathbb{R}$. Quindi non abbiamo di fronte un limite in più variabili, ma un limite “vecchio stile”.
- Osservando la formula che la definisce, potremmo dire che la derivata $\frac{\partial f}{\partial v}\left ( X \right )$ misura la variazione infinitesima di $f$ partendo da $X$ e spostandoci verso la direzione individuata da $V$, in rapporto allo spostamento effettuato.
- Le definizioni di derivata direzionale e di derivata parziale che abbiamo dato funzionano solo se i punti considerati hanno coordinate cartesiane, e se la funzione è definita in coordinate cartesiane. Se utilizzassimo altri sistemi di coordinate (come quelle polari, o quelle sferiche, o cilindriche) la definizione data sopra andrebbe riformulata.
- Non è assolutamente detto che le derivate direzionali o le derivate parziali di una funzione in un certo punto siano definite: sono pur sempre dei limiti, che - come ben sappiamo - possono anche non esistere.
Alcuni esempi di derivata direzionale
Prendiamo la funzione $f: \mathbb{R}^2 \rightarrow \mathbb{R}$ definita così: $$f(x, y) = -2x^2-2y^2-x+y+2$$Calcoliamo alcune derivate direzionali di $f$ nell’origine $O$. Il punto $V_1 = \left ( 1, 1 \right )$ determina una direzione $v_1$ lungo cui possiamo calcolare la derivata direzionale. Otteniamo: ##KATEX##\begin{aligned} \frac{\partial f}{\partial v_1}(O) & = \lim_{h \to 0} \frac{f \left ( 0 + h\cdot 1, 0 + h\cdot 1 \right )-f(0,0)}{h} = \\ & = \lim_{h \to 0} \frac{-2( 0 + h)^2 -2( 0 + h)^2 - (0+h) + (0+h) + 2 - 2}{h} = \\ & = \lim_{h \to 0} \frac{-4h^2}{h} = \lim_{h \to 0} (-4h) = 0 \end{aligned}##KATEX##Adesso invece prendiamo il punto $V_2 \equiv (1, -3)$, che determina un’altra direzione $v_2$. Abbiamo: ##KATEX##\begin{aligned} \frac{\partial f}{\partial v_2}(O) & = \lim_{h \to 0} \frac{f \left ( 0 + h\cdot 1, 0 + h\cdot (-3) \right )-f(0,0)}{h} = \\ & = \lim_{h \to 0} \frac{-2( 0 + h)^2 -2( 0-3h)^2 - (0+h) + (0-3h) + 2 - 2}{h} = \\ & = \lim_{h \to 0} \frac{-20h^2-4h}{h} = \lim_{h \to 0} (-20h-4) = -4 \end{aligned}##KATEX##Avremmo potuto anche calcolare le derivate direzionali rispetto alle stesse direzioni, ma in un altro punto: scegliamo $P \equiv \left ( -\frac{1}{4}, \frac{1}{4} \right)$. Otteniamo, dopo alcuni conti, che $$\frac{\partial f}{\partial v_1}(P) = \frac{\partial f}{\partial v_2}(P) = 0$$A dire il vero, è possibile mostrare che qualsiasi derivata direzionale in $P$ è nulla.
Dato che $f$ è una funzione che ha grafico in $\mathbb{R}^3$, possiamo interpretare geometricamente questi fatti. Questo ci aiuterà molto a capire che tipo di informazioni fornisce la derivata direzionale di una funzione di più variabili.
Il grafico di $f(x, y)$ è un paraboloide circolare:

Consideriamo la derivata direzionale $\frac{\partial f}{\partial v_1}(O)$. Questa derivata vale $0$: questo significa che, in prossimità dell’origine e lungo la direzione individuata da $v_1$, la funzione non cresce e non decresce. Per capire in che modo possiamo vedere questo dal grafico di $f$ bisogna ragionare in questo modo. Il vettore $v_1$ - che congiunge l’origine con $V_1$ - ha come direzione la retta passante per $O$ e $V_1$: questa retta non è altro che $r: \ y=x$. Vediamo l’immagine dei punti della retta $r$ tramite $f$, che disegna una curva sul grafico della funzione:
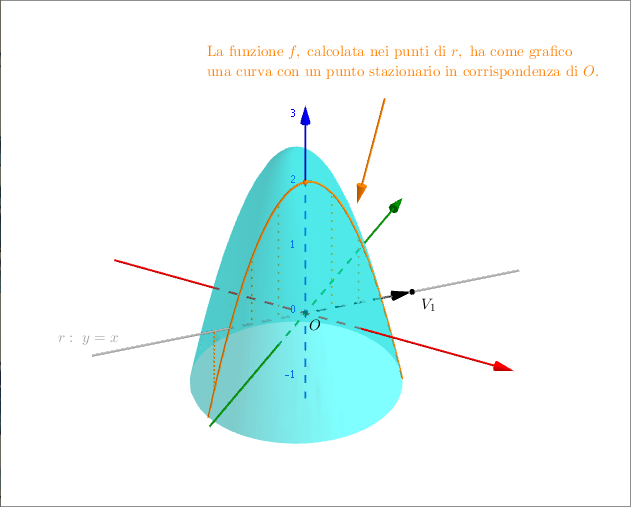
Si vede chiaramente che, in corrispondenza di $f(0,0) = 2$ (o meglio, di $(0,0,2)$) la curva ha un punto stazionario (un massimo in questo caso). Questo è coerente con il fatto che la derivata direzionale lungo $v_1$ valga $0$: sappiamo bene che i punti stazionari per una funzione sono proprio quelli che ne annullano la derivata, anche se qui - attenzione - non stiamo propriamente considerando la derivata di una funzione reale di variabile reale, ma una sua “parente stretta”.
Che dire del fatto che $\frac{\partial f}{\partial v_2}(O) = -4$? Semplicemente questo significa che la curva immagine della retta individuata da $v_2$ (che è $s: \ y = -3x$) decresce in prossimità di $O$, visto che la derivata direzionale ha valore negativo. Ecco infatti il grafico:

Spostiamoci adesso a controllare il comportamento della nostra funzione nel punto $P \equiv \left ( -\frac{1}{4}, \frac{1}{4} \right)$, dove tutte le derivate direzionali si annullano. Come forse si può intuire da quanto illustrato prima, questo significa che tutte le curve ottenute come immagine di una retta passante per $P$ (tramite $f$) hanno un punto stazionario in $f(P)$. In effetti, $f(P) = \frac{9}{4}$ (anzi, $\left ( -\frac{1}{4}, \frac{1}{4}, \frac{9}{4} \right )$ per essere precisi) è proprio la “sommità” del paraboloide:

Come vedremo, condizione necessaria e sufficiente affinché tutte le derivate direzionali di una funzione calcolate in un punto $P$ siano nulle è che tale punto sia stazionario per $P$: ovvero, $P$ potrà essere un minimo, un massimo o una sella per $f$, a seconda del determinante della matrice Hessiana calcolata in $P$. Chiaramente, se tutte le derivate direzionali sono nulle, significa banalmente che esse esistono: questo è equivalente ad affermare che la funzione è differenziabile in $P$.
Il calcolo delle derivate parziali
Sappiamo che per calcolare la derivata di una funzione di una variabile ci sono delle tecniche di calcolo molto efficienti, che permettono di ottenere un’espressione per la derivata senza dover ricorrere tutte le volte alla definizione di limite. Viene dunque da chiedersi se non esista una tecnica analoga che ci permetta di calcolare agevolmente le derivate direzionali di una funzione di più variabili.
Proviamo a ottenere qualche risultato studiando le derivate direzionali “più semplici possibili”, che sono le derivate parziali. Prendiamo una funzione $f: \mathbb{R}^n \rightarrow \mathbb{R}$ e supponiamo di voler calcolare la derivata parziale $\frac{\partial f}{\partial x_i}(P)$ per $1 \leq i \leq n$, definita a partire da un punto $W \equiv ( 0, 0, \ldots, w_i, \ldots, 0)$ sull’asse $x_i$, con $P \equiv (p_1, \ldots, p_n)$ nel dominio di $f$. Definiamo una nuova funzione $g_P$ a partire da $f$: ##KATEX##\begin{aligned} g_P: \mathbb{R} & \rightarrow \mathbb{R} \\ a & \mapsto f(p_1, p_2, \ldots, a, \ldots, p_n) \end{aligned}##KATEX##dove $a$ si trova all’$i$-esimo posto. Allora, per definizione di derivata, abbiamo:$$g_P’(p_i) = \lim_{t \to 0} \frac{g_P(p_i + t) - g_P(p_i)}{t}$$Esplicitando meglio questa formula otteniamo: ##KATEX##\begin{aligned}g_P’(p_i) & = \lim_{t \to 0} \frac{g_P(p_i + t) - g_P(p_i)}{t} = \\ & = \lim_{t \to 0} \frac{f(p_1, p_2, \ldots, p_i + t, \ldots, p_n) - f(p_1, \ldots, p_n)}{t} = \\ & = \lim_{h \to 0} \frac{f(p_1, p_2, \ldots, p_i + hw_i, \ldots, p_n) - f(p_1, \ldots, p_n)}{h} \end{aligned}##KATEX##dove nell’ultimo passaggio abbiamo effettuato la sostituzione $t = hw_i$. In sostanza abbiamo mostrato che $$g_P’(p_i)=\frac{\partial f}{\partial x_i}(P)$$Questo risultato giustifica la seguente importantissima regola:
Se vogliamo calcolare la derivata parziale di $f$ rispetto alla variabile $x_i$, possiamo considerare $f$ come se fosse una funzione della sola variabile $x_i$, e derivare rispetto a essa.
Facciamo un esempio: prendiamo la funzione $$f(x_1, x_2, x_3) = x_1^3x_2 - \ln(x_1) + \frac{x_1}{x_3}$$Ecco le sue derivate parziali: ##KATEX##\begin{aligned} \frac{\partial f}{\partial x_1} & = 3x_1^2 \cdot x_2 - \frac{1}{x_1} + \frac{1}{x_3} \\ \frac{\partial f}{\partial x_2} & = x_1^3 \\ \frac{\partial f}{\partial x_3} & = -\frac{x_1}{x_3^2} \end{aligned}##KATEX##Si vede quindi che il calcolo delle derivate parziali è un semplice calcolo di una derivata rispetto a una incognita, in cui “ignoriamo” le altre variabili (o meglio, le consideriamo come se fossero parametri, e non incognite).
A partire dal calcolo delle derivate parziali è possibile calcolare tutte le derivate direzionali che vogliamo, grazie al teorema del gradiente (quando sono rispettate le sue ipotesi).