Quando vogliamo descrivere un punto nel piano possiamo utilizzare, in particolare, due metodi: il sistema di coordinate cartesiane e il sistema di coordinate polari. Il primo è quello sicuramente più diffuso e che viene di solito utilizzato per descrivere gli oggetti della Geometria Analitica, come circonferenza, parabola, ellisse, iperbole e così via; il secondo invece è meno comune - specialmente nei primi anni delle scuole superiori - ma diventa fondamentale per esprimere la forma trigonometrica dei numeri complessi.
Come possiamo fare, invece, per descrivere i punti nello spazio euclideo? L’idea più semplice da cui partire è di prendere il vecchio sistema di coordinate cartesiane per il piano e visualizzarlo “immerso” nello spazio. I due assi $x$ e $y$ definiscono automaticamente un piano $Oxy$; immaginiamo poi di “aggiungere” un asse, sempre passante per l’origine $O$ e perpendicolare al piano $Oxy$, che permette sostanzialmente di descrivere la distanza di un qualsiasi punto dal piano dove giacciono gli assi $x$ e $y$. In questo modo abbiamo costruito il sistema di coordinate cartesiane nello spazio. Tradizionalmente, il nuovo asse prende il nome di asse $z$ (ma nessuno ci vieta di chiamare i tre assi in maniera diversa, come per esempio $x_1, x_2, x_3$).

Le coordinate cilindriche
Cosa sarebbe successo se fossimo partiti dal sistema di coordinate polari invece di considerare il sistema di coordinate cartesiane sul piano? Possiamo farlo tranquillamente: in più, nessuno ci impedisce di “aggiungere” l’asse $z$ anche in questo caso. Ciascuna terna $(R, \Theta, z)$ descriverà un punto dello spazio: gli unici punti che non potranno essere descritti in questo modo sono quelli dell’asse $z$, dato che per essi $\Theta$ non è definito. Per questi punti in genere si preferisce indicare solamente la coordinata $z$ ricordando che $R=0$.
Quello che abbiamo appena costruito si chiama sistema di coordinate cilindriche.

Sottolineiamo che le restrizioni su $R$ e $\Theta$ presenti per le coordinate polari sono ancora valide: quindi anche per le coordinate cilindriche $R$ deve essere non negativo e $\Theta$ deve essere compreso nell’intervallo $[0, 2\pi)$.
Il motivo per cui queste coordinate sono chiamate “cilindriche” è che è particolarmente semplice descrivere un cilindro in questo contesto. Per esempio, un cilindro $C$ di altezza $h$ e che ha per base inferiore un cerchio di raggio $a$ e di centro $O$ sul piano $Oxy$, può essere descritto da così: $$C: \quad \begin{cases} R \leq a \\ 0 \leq z \leq h \end{cases}$$
Le coordinate sferiche
Adesso definiamo un altro sistema di coordinate nello spazio, un po’ diverso da quelli visti finora. Scegliamo un piano $\alpha$ nello spazio e una semiretta $a$ che giace su di esso: chiamiamo $O$ l’origine di tale semiretta. Conduciamo inoltre una semiretta orientata $b$ perpendicolare ad $\alpha$ con origine in $O$ (se ne possono costruire due: basta sceglierne una).

Vogliamo descrivere un qualsiasi punto $P$ dello spazio a partire da questa costruzione. Per prima cosa conduciamo la retta perpendicolare ad $\alpha$ passante per $P$ (eventualmente la retta è ridotta al solo punto $P$, se $P \in \alpha$); chiamiamo $P’$ il punto di intersezione tra questa retta e il piano $\alpha$. Inoltre:
- chiamiamo $\theta$ la misura dell’angolo compreso tra il segmento $OP’$ e la semiretta $a$;
- indichiamo con $r$ la misura del segmento $PO$;
- chiamiamo $\phi$ la misura dell’angolo compreso tra il segmento $PO$ e la semiretta $b$.
Ogni terna $(r, \theta, \phi)$ identifica completamente un punto $P$ nello spazio. Gli unici punti che non possono essere indicati con una terna del genere sono quelli della semiretta $b$ o del suo prolungamento, dato che $\theta$ non è definito (similmente a quanto accade per i punti dell’asse $z$ per le coordinate cilindriche). Generalmente un punto di questo tipo viene rappresentato indicando solo $r$ e $\phi$, che può essere $0$ o $\pi$ a seconda che il punto sia su $b$ o sul suo prolungamento, rispettivamente (per l’origine $O$ nemmeno $\phi$ è definito: quello sarà il punto corrispondente a $r=0$).
Abbiamo quindi costruito un nuovo sistema di coordinate nello spazio, che chiamiamo sistema di coordinate sferiche.
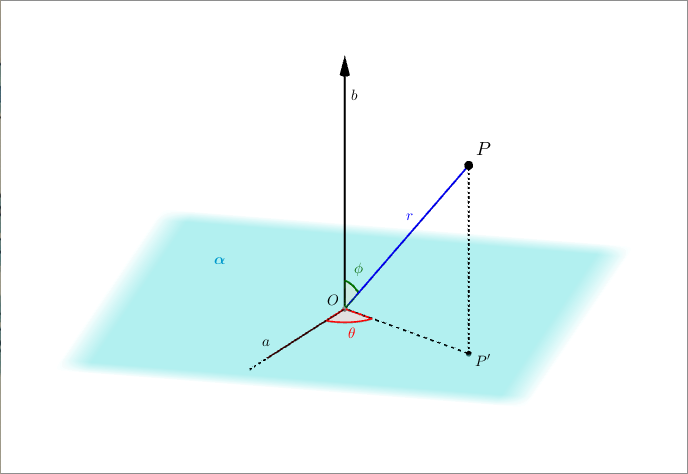
Dalla definizione che abbiamo appena dato deduciamo le seguenti limitazioni su $r$, $\theta$ e $\phi$: ##KATEX##\begin{aligned} & r \geq 0 \\ & \theta \in [0, 2\pi) \\ & \phi \in [0, \pi] \end{aligned}##KATEX##Il nome “coordinate sferiche” non è casuale: in queste coordinate una sfera $S$ centrata nell’origine $O$ e di raggio $a$ è descritta semplicemente dalla condizione $$S: \quad r \leq a$$
Come passare da un sistema di coordinate a un altro
In maniera analoga a quanto fatto quando abbiamo introdotto il sistema di coordinate polari, vogliamo scrivere le coordinate di un punto nello spazio in qualsiasi sistema di coordinate conoscendone l’espressione che aveva in uno degli altri due.
Sottolineiamo alcune convenzioni molto importanti che adotteremo.
- L’origine $O$ sarà sempre lo stesso punto per tutti i sistemi di coordinate considerati.
- L’asse $x$ delle coordinate cartesiane coinciderà sempre con la semiretta a partire da cui si definisce l’angolo $\Theta$ nelle coordinate cilindriche.
- L’asse $x$ delle coordinate cartesiane coinciderà sempre con la semiretta $a$ delle coordinate sferiche. Inoltre, la semiretta $b$ di tali coordinate coinciderà sempre con il semiasse positivo delle $z$.
- La semiretta $a$ e la semiretta che si usa per definire $\theta$ nelle coordinate cilindriche concideranno sempre.
Il motivo per cui imponiamo queste condizioni è che nel caso in cui i sistemi di coordinate fossero posizionati in maniera generica l’uno rispetto all’altro le formule che seguono sarebbero enormemente più complicate. In ogni caso tutte le formule che scriveremo non avranno dimostrazione; segnaliamo però che per ricavarle è sufficiente applicare in maniera adeguata alcune formule trigonometriche e conoscere le definizioni di funzioni trigonometriche inverse.
- Coordinate cartesiane $\rightarrow$ coordinate sferiche
$P \equiv (x, y, z), \quad$ $x \neq 0$, $y \neq 0$ $$P \equiv \begin{cases} r = \sqrt{x^2 + y^2 + z^2} \\ \theta = \arctan \left ( \frac{y}{x} \right ) \\ \phi = \arccos \left ( \frac{z}{\sqrt{x^2+y^2+z^2}} \right ) \end{cases}$$ $P \equiv (0, y, z), \quad$ $y \neq 0$ $$P \equiv \begin{cases} r = \sqrt{y^2 + z^2} \\ \theta = \frac{\pi}{2} \vee \theta = \frac{3\pi}{2} \\ \phi = \arccos \left ( \frac{z}{\sqrt{y^2+z^2}} \right ) \end{cases}$$Scegliamo $\frac{\pi}{2}$ o $\frac{3\pi}{2}$ a seconda che $y>0$ o $y<0$, rispettivamente. $P \equiv (0, 0, z), \quad$ $z \neq 0$ $$P \equiv \begin{cases} r = |z| \\ \phi = 0 \vee \phi = \pi \end{cases}$$Scegliamo $0$ oppure $\pi$ a seconda che $z>0$ o $z<0$, rispettivamente. $P \equiv (0,0,0) \equiv O$ $$P: \ r=0$$ - Coordinate cilindriche $\rightarrow$ coordinate sferiche
Prima di tutto ricordiamo che le origini $O$ di entrambi i sistemi di coordinate coincidono. Ecco, invece, le formule di conversione per tutti gli altri punti.$P \equiv (R, \Theta, z), \quad$ $R \neq 0$, $z \neq 0$ $$P \equiv \begin{cases} r = \sqrt{R^2 + z^2} \\ \theta = \Theta \\ \phi = \arctan \left ( \frac{R}{z} \right ) \end{cases}$$ $P \equiv (R, \Theta, 0), \quad$ $R \neq 0$ $$P \equiv \begin{cases} r = R \\ \theta = \Theta \\ \phi = \frac{\pi}{2} \end{cases}$$ $P$ con coordinate $R=0$ e $z \neq 0$, (asse $z$) $$P \equiv \begin{cases} r = |z| \\ \phi = 0 \vee \phi = \pi \end{cases}$$Scegliamo $0$ oppure $\pi$ a seconda che $z>0$ o $z<0$, rispettivamente. - Coordinate cilindriche $\rightarrow$ coordinate cartesiane
$P \equiv (R, \Theta, z), \quad$ $R \neq 0$ $$P \equiv \begin{cases} x = R\cos(\Theta) \\ y = R \sin (\Theta) \\ z = z \end{cases}$$ $P$ con coordinate $R=0$ e $z$ (asse $z$) $$P \equiv \begin{cases} x=0 \\ y = 0 \\ z = z \end{cases}$$ - Coordinate sferiche $\rightarrow$ coordinate cartesiane
Come al solito, l’origine di un sistema di coordinate coincide con l’origine dell’altro. Inoltre:$P \equiv (r, \theta, \phi), \quad$ $\phi \neq 0 \wedge \phi \neq \pi$ $$P \equiv \begin{cases} x =r\sin(\phi)\cos(\theta) \\ y = r\sin(\phi)\sin(\theta) \\ z = r\cos(\phi) \end{cases}$$ $P$ con coordinate $r$ e $\phi = 0 \vee \phi = \pi$ (asse $z$) $$P \equiv \begin{cases} x =0 \\ y = 0 \\ z = r\cos(\phi) \end{cases}$$ - Coordinate cartesiane $\rightarrow$ coordinate cilindriche
$P \equiv (x, y, z), \quad$ $x \neq 0, y \neq 0$ $$P \equiv \begin{cases} R = \sqrt{x^2 + y^2 } \\ \Theta = \arctan \left ( \frac{y}{x} \right ) \\ z = z \end{cases}$$ $P \equiv (0, y, z), \quad$ $y \neq 0$ $$P \equiv \begin{cases} R = |y| \\ \Theta = \frac{\pi}{2} \vee \Theta = \frac{3\pi}{2} \\ z = z \end{cases}$$Scegliamo $\frac{\pi}{2}$ o $\frac{3\pi}{2}$ a seconda che $y>0$ o $y<0$, rispettivamente. $P \equiv (0,0,z)$ $P$ è sull’asse $z$ e ha coordinata $z$. - Coordinate sferiche $\rightarrow$ coordinate cilindriche
Di nuovo, ricordiamo che le origini dei due sistemi di coordinate coincidono. Inoltre:$P \equiv (r, \theta, \phi), \quad$ $\phi \neq 0 \wedge \phi \neq \pi$ $$P \equiv \begin{cases} R = r\sin(\phi) \\ \Theta = \theta \\ z = r\cos(\phi) \end{cases}$$ $P$ con coordinate $r$ e $\phi = 0 \vee \phi = \pi$ (asse $z$) $$P \equiv \begin{cases} R = 0 \\ z = r\cos(\phi) \end{cases}$$
Questi cambiamenti di coordinate risultano molto utili nel calcolo di integrali multipli.