La circonferenza è una delle coniche più famose, a causa delle numerose proprietà che la caratterizzano: basti pensare, per esempio, alle proprietà degli angoli che hanno vertice nel centro della circonferenza e sulla circonferenza stessa, o alle proprietà dei poligoni inscritti e circoscritti. Ricordiamo, in ogni caso, che possiamo definire questa conica come un luogo geometrico:
Definizione
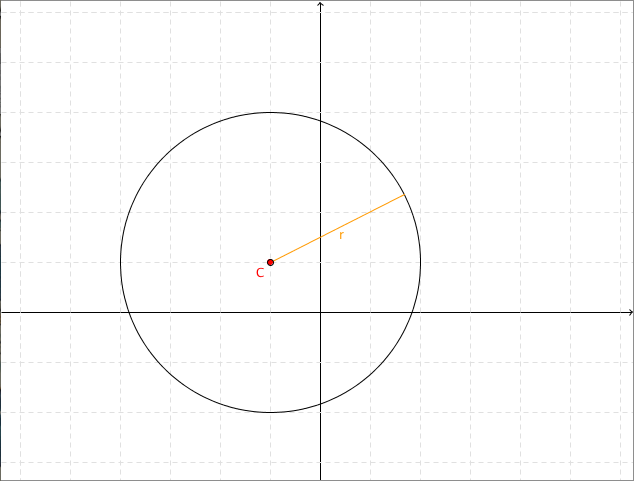
Prendiamo un punto $C$ nel piano e scegliamo un numero non negativo $r$. L’insieme dei punti del piano che distano $r$ dal punto $C$ è detto circonferenza.
Il punto $C$ è detto centro della circonferenza, mentre $r$ è il raggio della circonferenza.
Se il punto $C$ ha coordinate $(x_C, y_C)$ nel piano cartesiano allora l’equazione in forma implicita della circonferenza è la seguente: $$(x-x_C)^2 + (y-y_C)^2 = r^2$$È abbastanza immediato vedere che questa equazione discende dalla formula per la distanza tra due punti.
Un altro modo per rappresentare l’equazione di una circonferenza è di utilizzare l’equazione in forma esplicita: $$x^2+y^2+ax+by+c=0, \qquad a^2+ b^2-4c > 0$$La richiesta $a^2+ b^2-4c > 0$, detta anche condizione di realtà della circonferenza, è necessaria per far sì che l’equazione descriva effettivamente un insieme di punti nel piano cartesiano. Se invece $a^2+ b^2-4c = 0$ la circonferenza si riduce a un solo punto (circonferenza degenere) e se $a^2+ b^2-4c < 0$ la circonferenza non esiste del tutto (o meglio, l’equazione non descrive una circonferenza, perché non esistono punti del piano cartesiano che la soddisfino).
A partire dalla circonferenza descritta in forma esplicita, possiamo ricavare le seguenti formule.
Raggio: $$r = \sqrt{ \left ( \frac{a}{2} \right )^2 + \left ( \frac{b}{2} \right )^2 - c}.$$
Coordinate del centro: $$C \equiv \left ( - \frac{a}{2}, -\frac{b}{2} \right )$$
Vale la pena di sottolineare che la condizione di realtà ci garantisce che la formula per determinare il raggio abbia senso (se non fosse valida, avremmo un numero nullo o negativo sotto radice).
Tangenti a una circonferenza
Supponiamo di voler determinare le equazioni delle rette passanti per un punto $T \equiv (x_T, y_T)$ e che siano tangenti a una circonferenza data (che d’ora in poi considereremo espressa in forma esplicita $x^2+y^2+ax+by+c=0$). Abbiamo tre casi distinti che dobbiamo analizzare.
- Se il punto $T$ è interno alla circonferenza, non ci sono rette tangenti.
- Se $T$ appartiene alla circonferenza possiamo utilizzare la formula di sdoppiamento per determinare l’equazione dell’unica retta tangente alla circonferenza passante per $T$: $$r: xx_T + yy_T + a\frac{x+x_T}{2} + b\frac{y+y_T}{2} + c=0$$In effetti, ricordando che $x_T$, $y_T$, $a$, $b$, $c$ sono numeri, questa è un’equazione di primo grado in $x$ e $y$ che rappresenta proprio una retta nel piano cartesiano.
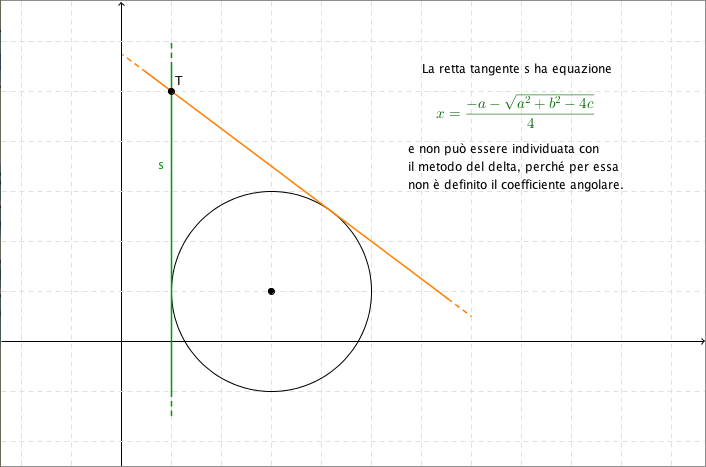
Inoltre, il coefficiente angolare di questa retta esiste quando $y_T \neq -\frac{b}{2}$ ed è: $$m = -\frac{2x_T+a}{2y_T+b}.$$ - Se $T$ è un punto esterno alla circonferenza, le rette tangenti alla circonferenza passanti per $T$ sono sempre due. Per ottenere i coefficienti angolari di queste rette è sufficiente risolvere il sistema tra l’equazione della circonferenza e il fascio di rette passante per $T$, imponendo che l’equazione risolvente abbia $\Delta = 0$ (come viene spiegato in questo video).
Bisogna comunque stare attenti: nel caso in cui il punto $T$ abbia ascissa: $$x_T = \frac{-a \pm \sqrt{a^2+b^2-4c}}{4}$$il metodo del delta ci fornirà un solo coefficiente angolare, perché l’altra retta tangente sarà proprio la retta verticale passante per $T$.