In fisica le grandezze non sono tutte dello stesso tipo e, a seconda delle loro caratteristiche, possono essere suddivise in due grandi categorie: scalari o vettoriali.
Le grandezze scalari sono quelle grandezze che possono essere descritte solo con un numero e un’unità di misura. Quel numero rappresenta la loro misura. Sono esempi di grandezze scalari il tempo, la temperatura, la massa.
Le grandezze vettoriali, invece, sono quelle grandezze per cui non è sufficiente un numero e un’unità di misura per definirle. Occorre anche una direzione e un verso. Sono grandezze vettoriali, appunto, tutte le grandezze fisiche che possono essere identificate da un vettore.
Un vettore è, in parole povere, una freccia. Più precisamente, in matematica si definisce come vettore una classe di segmenti orientati equipollenti, ossia l’insieme di tutti i segmenti dotati di medesima lunghezza, direzione e verso. I vettori solitamente si indicano con lettere latine in grassetto, con sopra una freccia: $\vec{v}$.
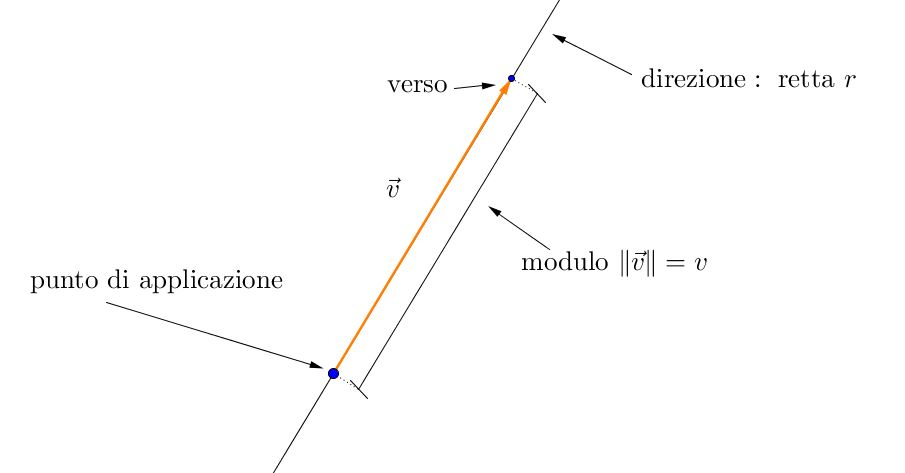
- Il modulo di un vettore è la sua lunghezza, e si indica con $\| \vec{v} \|$, $| \vec{v} |$, o semplicemente $v$. In fisica, il modulo di un vettore si identifica con un numero e un’unità di misura. Per esempio, il modulo di una velocità si misura in metri al secondo, $\text{m } / \text{s}$.
- La direzione di un vettore è la retta (geometrica) su cui giace il segmento. Se mi sposto di tre metri verso destra, per esempio, la direzione dello spostamento sarà la retta che congiunge un punto direttamente alla mia sinistra con un punto direttamente alla mia destra.
- Il verso di un vettore è il verso in cui la direzione del vettore viene percorsa, cioè l’orientazione del segmento che definisce il vettore. Lo spostamento di prima poteva anche essere svolto verso sinistra: la direzione sarebbe rimasta la medesima, mentre sarebbe cambiato il verso.
Caso particolare è il vettore nullo, ossia un vettore di modulo $0$. Per il vettore nullo non è possibile definire una direzione (e dunque nemmeno un verso), poichè il vettore nullo si riduce solo a un punto, e per un punto passano infinite rette.
Esempi di grandezze vettoriali sono la velocità, lo spostamento, l’accelerazione, il campo elettrico, le forze.
Quando una grandezza vettoriale è applicata ad un punto di un corpo o dello spazio, si deve anche indicare il suo punto di applicazione. (Questa è la principale differenza tra un vettore che rappresenta una grandezza fisica e un vettore come ente matematico).
In generale, due grandezze possono essere sommate o sottratte solo se sono omogenee, ossia se hanno la stessa unità di misura. Le grandezze scalari possono essere sommate tra loro secondo le usuali regole dell’algebra. Le grandezze vettoriali, invece, si comportano in modo differente, come spiegato nella prossima lezione.