Lo studio delle grandezze fisiche introduce un nuovo ente matematico: i vettori. Come tra i numeri (detti in questo contesto scalari), tra i vettori si possono effettuare delle operazioni, come la somma (vettoriale) e il prodotto (vettoriale). Queste operazioni però sono totalmente diverse da quelle prescritte dall’algebra e dall’aritmetica, e andiamo qui di seguito a illustrarle.
Somma di vettori
Ci sono principalmente due modi per calcolare la somma tra due vettori: il metodo punta-coda e il metodo del parallelogramma. La somma di due vettori sarà comunque sempre un vettore.
Metodo punta-coda: Tenendo fissato un vettore (in questo caso $\vec{a}$), si trasporta l’altro (che qui per noi è $\vec{b}$), mantendolo sempre parallelo a se stesso, in modo tale che il suo punto di applicazione coincida con la punta del primo vettore. Il vettore somma $\vec{a} + \vec{b}$ è allora il vettore che congiunge la “coda del primo vettore”, ossia il suo punto di applicazione, con la “punta del secondo vettore”, come mostrato in figura:

Metodo del Parallelogramma: per applicare questo metodo, occorre costruire un parallelogramma di lati i vettori dati. La somma dei due vettori è la diagonale del parallelogramma che parte dal punto di applicazione di uno dei due, e arriva alla punta di uno dei due, come mostrato in figura:

Differenza di due vettori
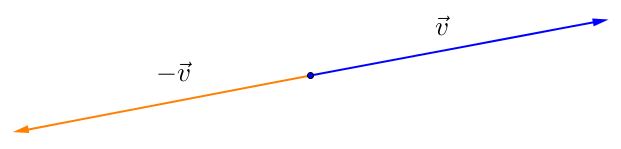
Come nell’algebra usuale, l’operazione inversa alla somma è la differenza. Per calcolare la differenza $ \vec{a} - \vec{b}$ di due vettori $\vec{a}$, $\vec{b}$, è utile prima calcolare l’opposto di un vettore: dato un vettore $\vec{v}$, il suo opposto $-\vec{v}$ è quel vettore che ha medesimo modulo e direzione, ma verso contrario:
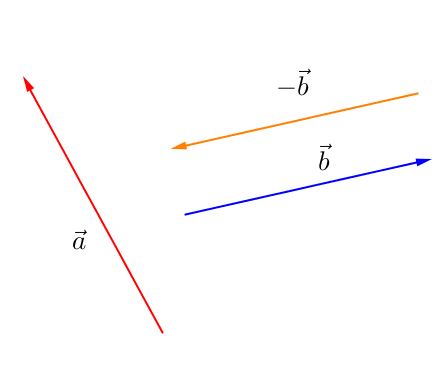
Ciò detto, la differenza tra $\vec{a}$ e $\vec{b}$ è la somma vettoriale tra $\vec{a}$ e l’opposto di $\vec{b}$, $-\vec{b}$:
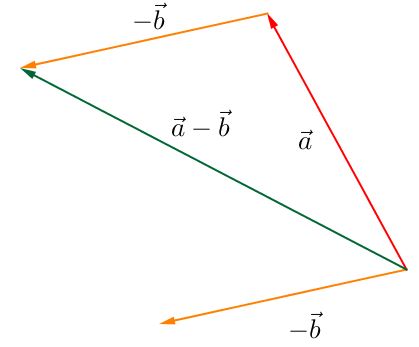
Usando la regola del parallelogrammo, è facile identificare la differenza di due vettori: si tratta dell’altra diagonale rispetto a quella usata per costruire la somma. Questa diagonale identifica modulo e direzione; il verso di $\vec{a} - \vec{b}$ è quello che dalla punta di $\vec{b}$ punta verso la punta di $\vec{a}$:

Come accade per i numeri, la differenza non è un’operazione commutativa. Vale però una regola del tutto analoga a quella dell’algebra ordinaria: $\vec{a} - \vec{b} = - (\vec{b} - \vec{a})$
Uno scalare $\lambda$ e un vettore $\vec{v}$ possono essere tra loro moltiplicati: posso considerare un multiplo di un vettore per uno scalare $\lambda \cdot \vec{v}$; questo è un vettore avente:
- per direzione la medesima del vettore dato;
- per verso il medesimo del vettore dato se lo scalare è positivo, o verso opposto se lo scalare è negativo;
- modulo pari al modulo del vettore di partenza, moltiplicato per il modulo dello scalare.
Per esempio, $2 \cdot \vec{v}$ è un vettore lungo il doppio di $\vec{v}$, avente stessa direzione e stesso verso; mentre $- 2 \cdot \vec{v}$ ha modulo pari al doppio di $\vec{v}$, stessa direzione ma verso opposto a quello di $\vec{v}$.

Questo prodotto eredita alcune proprietà dell’algebra ordinaria. Ad esempio: $ 2 \cdot \vec{v} = \vec{v} + \vec{v}$, $(-4)\cdot \vec{v} = -(4 \cdot \vec{v})$, eccetera.
Quando sia chiaro chi è il vettore e chi lo scalare, spesso si omette il punto, scrivendo $\lambda \vec{v}$ invece di $\lambda \cdot \vec{v}$.
Un metodo più generale per effettuare somma e differenza di due vettori, e molto utile per le operazioni di prodotto scalare e vettoriale definite in seguito, è quello di scomporre un vettore in componenti.
Si definisce un versore come un vettore di modulo $1$. Nel piano cartesiano identifichiamo due versori particolari: $\mathbf{i}$ e $\mathbf{j}$. Questi versori indicano un vettore unitario, situato rispettivamente sull’asse $x$ il versore $\mathbf{i}$ o sull’asse $y$ il versore $\mathbf{j}$, di verso positivo. Nello spazio euclideo tridimensionale, si aggiunge il versore $\mathbf{k}$, posto lungo l’asse $z$, di lunghezza $1$ e verso positivo.

Una volta identificati i versori, ogni vettore che vive nel piano cartesiano può essere scritto come somma di due vettori paralleli ai versori $\mathbf{i}$ e $\mathbf{j}$, dette componenti del vettore:

Ci sono diversi modi di scrivere un vettore in componenti: si può scrivere come somma di vettori, ad esempio $\vec{a} = 2 \mathbf{i} + 3\mathbf{j}$, oppure indicandone le componenti solo come scalari, in colonna o separati da una virgola: $\left( \begin{array}{c} 2 \\ 3 \end{array} \right) = (2,3)$.
La somma o la differenza di vettori si può dunque eseguire componente per componente: si sommano cioè le componenti orizzontale e verticale dei singoli vettori tra di loro, come se si trattasse di una somma algebrica di monomi simili.
Per esempio, siano dati i vettori $\vec{a} = \mathbf{i} + 2\mathbf{j}$ e $vec{b} = 2 \mathbf{i} + \mathbf{j}$. Allora $\vec{a} + \vec{b} =$ $\mathbf{i} + 2\mathbf{j} + 2\mathbf{i} + \mathbf{j} =$ $3\mathbf{i} + 3\mathbf{j}$, cioè il vettore somma avrà componenti $\left( \begin{array}{c} 3 \\ 3 \end{array} \right)$; mentre la differenza $\vec{a} - \vec{b}$ si calcola come $\mathbf{i} + 2\mathbf{j} -( 2\mathbf{i} + \mathbf{j}) =$ $\mathbf{i} + 2\mathbf{j} - 2\mathbf{i} - \mathbf{j} =$ $-\mathbf{i} +\mathbf{j}$, ossia $\left( \begin{array}{c} -1 \\ 1 \end{array} \right)$.

Ora definiamo due tipi di prodotti tra vettori. Si distinguono in base al tipo di grandezza cui appartiene il risultato: si parla di prodotto scalare e prodotto vettoriale quindi, a seconda che il risultato del prodotto sia appunto uno scalare o un vettore.
Il prodotto scalare tra due vettori restituisce sempre uno scalare. Siano $\vec{a}$ e $\vec{b}$ due vettori, e $\alpha$ l’angolo convesso tra essi compreso; il prodotto scalare tra $\vec{a}$ e $\vec{b}$ è allora $$ \vec{a} \cdot \vec{b} = | \vec{a} | \ | \vec{b} | \cos(\alpha) $$

Si può notare che il prodotto scalare rappresenta l’area (con segno) del rettangolo ottenuto proiettando uno dei due vettori ortogonalmente sull’altro:

Siccome la proiezione di un vettore ortogonale ad un’altro vettore (cioè $\alpha = 90 ^\circ$) è solo un punto, il prodotto scalare di due vettori le cui direzioni siano perpendicolari è nullo:
$$ \vec{a} \cdot \vec{b} = 0 \Leftrightarrow \vec{a} \perp \vec{b}$$
Con queste presrcizioni è facile calcolare il prodotto scalare dei vari versori fondamentali:
$$ \mathbf{i} \cdot \mathbf{i} = \mathbf{j} \cdot \mathbf{j} = \mathbf{k} \cdot \mathbf{k} = 1 $$
$$ \mathbf{i} \cdot \mathbf{j} = \mathbf{j} \cdot \mathbf{k} = \mathbf{k} \cdot \mathbf{i} = 0 $$
Il prodotto scalare è commutativo e gode della proprietà distributiva rispetto alla somma vettoriale:
$$ \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} $$
$$ \vec{a} \cdot \left( \vec{v} + \vec{w} \right) = \vec{a} \cdot \vec{v} + \vec{a} \cdot \vec{w} $$
Come si può dedurre dalla sua definizione, il prodotto scalare di un vettore per se stesso restituisce la sua norma al quadrato: $ \vec{a} \cdot \vec{a} = | \vec{a} | ^2$.
Il prodotto vettoriale fra due vettori restituisce sempre un vettore. Dati due vettori $\vec{a}$ e $\vec{b}$ (in quest’ordine), sia $\alpha$ l’angolo convesso tra di essi compreso.
Definiamo allora il prodotto vettore tra $\vec{a}$ e $\vec{b}$ come quel vettore $\vec{a} \times \vec{b}$ (o, a volte, $\vec{a} \wedge \vec{b}$) che possiede:
- modulo pari all’area del palallelogrammo avente per lati i due vettori:
$ | \vec{a} \times \vec{b} | = |\vec{a}| \ |\vec{b}| \ | \sin(\alpha) | $ - direzione perpendicolare al piano individuato dai due vettori
- verso indicato dalla cosiddetta “regola della mano destra”: disponiamo pollice, indice e medio in modo tale che essi risultino tra loro perpendicolari. In questo caso abbiamo l’indice che mostra verso e direzione del vettore $\vec{a}$, il medio che è disposto secondo il verso e la direzione di $\vec{b}$ e il pollice che rappresenta direzione e verso di $\vec{a} \times \vec{b}$

Nel caso in cui due vettori siano ortogonali (cioè se $\vec{a} \perp \vec{b}$, $\alpha = 90 ^\circ$ o $270^\circ$), il prodotto vettore non si annulla, come nel caso del prodotto scalare: in questo caso anzi il suo modulo è esattamente il prodotto dei moduli.
Il prodotto vettore invece si annulla se i due vettori di partenza hanno direzioni tra loro parallele:
$$ \vec{a} \times \vec{b} = 0 \Leftrightarrow \vec{a} \parallel \vec{b} $$
Con queste regole, è facile calcolare il prodotto vettore dei versori fondamentali:
$$ \mathbf{i} \times \mathbf{i} = \mathbf{j} \times \mathbf{j} = \mathbf{k} \times \mathbf{k} = 0 $$
$$ \mathbf{i} \times \mathbf{j} = \mathbf{k}; \mathbf{k} \times \mathbf{i} = \mathbf{j}; \mathbf{j} \times \mathbf{k} = \mathbf{i} $$
Il prodotto vettore non è commutativo: gode della proprietà antisimmetrica, ossia $\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}$.
Credits immagini: Wikicommons, Svjo, Candlemon, Oleg Alexandrov