Punti di discontinuità di una funzione: classificazione

Sappiamo che una funzione reale di variabile reale può essere continua: questo accade quando, intuitivamente, possiamo disegnarne il grafico sul piano cartesiano “senza staccare la matita dal foglio”, ovvero se il grafico è una linea continua.
Le funzioni continue sono molto comode da studiare, ma non sono poi così frequenti: anzi, capita spesso di incontrare funzioni con problemi di continuità in uno o più punti. È quindi necessario studiare a fondo le tipologie di discontinuità che una funzione può avere, e fornirne una classificazione.

Definizione

Consideriamo una funzione $f(x)$ e un qualsiasi punto $x_0 \in \mathbb{R}$. Diremo che $f(x)$ ha una discontinuità di prima specie in $x_0$ se esistono i limiti $$\lim_{x \to x_0^-} f(x), \qquad \lim_{x \to x_0^+} f(x)$$e sono entrambi finiti, ma diversi.
La discontinuità di prima specie viene chiamata anche discontinuità con salto, dato che il grafico di una funzione con questo tipo di discontinuità “salta” da un’ordinata a un’altra in corrispondenza del punto di discontinuità.

L’esempio classico per la discontinuità di prima specie è dato dalla funzione segno $f(x) = \text{sgn}(x)$, che in $x=0$ ha proprio una discontinuità di questo tipo. Il “salto” vale esattamente $2$, dato che $$\lim_{x \to 0^-}\text{sgn}(x) = -1, \qquad \lim_{x \to 0^+}\text{sgn}(x) = 1$$Possiamo costruire una discontinuità di prima specie molto facilmente utilizzando una funzione definita a tratti, come questa: $$f(x) = \begin{cases} 2x-3 & \text{se }x \geq 0 \\ -x+1 & \text{se }x < 0 \end{cases}$$Il grafico di questa funzione ha una discontinuità con salto in $0$, che è il punto in cui i due rami della funzione vengono “incollati”.

 
Definizione

Consideriamo una funzione $f(x)$ e un qualsiasi punto $x_0 \in \mathbb{R}$. Se almeno uno tra i due limiti $$\lim_{x \to x_0^-} f(x), \qquad \lim_{x \to x_0^+} f(x)$$ non esiste, oppure è infinito, diremo che $f(x)$ ha una discontinuità di seconda specie in $x_0$.

Le discontinuità di seconda specie sono molto frequenti, anche tra le funzioni elementari. Per esempio, la funzione trigonometrica $f(x) = \tan(x)$ ha infiniti punti di discontinuità di seconda specie in $\frac{\pi}{2} + k \pi$ con $k \in \mathbb{Z}$, dato che per ogni $k$ vale: $$\lim_{x \to \frac{\pi}{2}^- + k \pi} \tan(x) = +\infty, \qquad \lim_{x \to \frac{\pi}{2}^+ + k \pi} \tan(x) = -\infty$$Ci sono casi ben più complessi: per esempio prendiamo la funzione $$f(x) = \frac{1}{x} \sin \left ( e^{\frac{1}{x}} + \frac{\pi}{2} \right )$$Osserviamo che $$\lim_{x \to 0^-} f(x) = \underbrace{\sin \left ( 0 + \frac{\pi}{2} \right )}_{ = \ 1} \cdot \lim_{x \to 0^-} \frac{1}{x} = - \infty $$mentre il limite destro (cioè per $x \to 0^+$) non esiste. Il punto $0$ rientra a pieno titolo tra i punti di discontinuità di seconda specie per $f(x)$.

Definizione

Prendiamo una funzione $f(x)$ e un qualsiasi punto $x_0 \in \mathbb{R}$. Se esiste ed è finito il limite $$\lim_{x \to x_0} f(x) = l$$ma $f(x_0)$ non esiste oppure $f(x_0) \neq l$, allora $x_0$ è una discontinuità di terza specie per $f(x)$.
L’esistenza del limite finito $l$ garantisce che, nelle vicinanze di $x_0$, la funzione sia “quasi continua”; il fatto che però $l$ non coincida con il valore della funzione in $x_0$ (o che addirittura questo valore non esista) è equivalente ad affermare che il grafico ha un “buco” in $x_0$. Per questo motivo la discontinuità di terza specie è anche detta discontinuità eliminabile: basterebbe “riempire” il buco che c’è nel grafico di $f(x)$ in corrispondenza di $x_0$ assegnando $f(x_0) = l$.

Una funzione che presenta una discontinuità di terza specie è $$f(x) = \frac{x^2}{x}$$Questa funzione, nonostante la tentazione di semplificare numeratore e denominatore sia forte, non è uguale alla retta $y = x$ dato che $f(x)$ non è definita in $x = 0$; inoltre $$\lim_{x \to 0^-} \frac{x^2}{x} = \lim_{x \to 0^+} \frac{x^2}{x} = 0$$il che mostra come $f(x)$ abbia una discontinuità eliminabile in $0$. In effetti il grafico di $f(x)$ è proprio la bisettrice del primo e del terzo quadrante con un “buco” nell’origine.

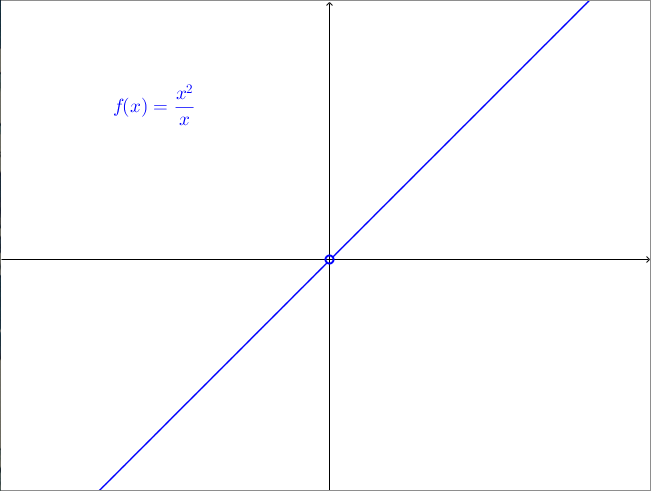
Facciamo alcune osservazioni relativamente alle definizioni che abbiamo appena dato.

• Soltanto quando dobbiamo controllare se c’è una discontinuità eliminabile ha senso controllare il valore che la funzione assume nel punto in cui stiamo guardando. Negli altri due casi invece questo non è assolutamente importante.
• Il punto di cui vogliamo classificare il tipo di discontinuità può appartenere o non appartenere al dominio della funzione con cui stiamo lavorando, ma non ci sono particolari richieste a riguardo.
• Da un certo punto di vista, la discontinuità di seconda specie è una specie di “contenitore” delle discontinuità più particolari e “patologiche”. In effetti, la discontinuità con salto e la discontinuità eliminabile si verificano in condizioni abbastanza regolari: il limite destro e il limite sinistro devono esistere finiti, e si ha una o l’altra discontinuità a seconda che siano diversi o uguali.
• Sfruttando le osservazioni fatte nei punti precedenti, potremmo stilare una specie di “guida intelligente” da seguire quando si vuole controllare che discontinuità ha una funzione $f(x)$ in un punto $x_0$.
  1. Se anche uno solo tra $\displaystyle \lim_{x \to 0^-}f(x)$ e $\displaystyle \lim_{x \to 0^+}f(x)$ è infinito o non esiste, allora la discontinuità è di seconda specie.
  2. Se i limiti sono entrambi finiti, ma diversi, allora la discontinuità è di prima specie.
  3. Nel caso invece i limiti siano finiti e uguali a $l$, allora è necessario controllare se $f(x)$ è definita o no in $x_0$; se non lo è, o se lo è e $f(x_0) \neq l$, abbiamo una discontinuità di terza specie.
  4. Se tutti i controlli che abbiamo fatto hanno dato esito negativo, dobbiamo concludere che $f(x_0)$ è continua in $x_0$.

Abbiamo classificato e discusso tutte le tipologie di punto di discontinuità. Ma come facciamo a trovarli? Cioè: come si fa a capire quando una funzione non è continua?

Esistono principalmente due “campanelli d’allarme” che ci possono far intuire la presenza di punti di discontinuità.

• Tutti i punti che non appartengono al dominio della funzione sono buoni candidati a essere punti di discontinuità, a patto che non si trovino ai bordi del dominio.
• Se la funzione che stiamo analizzando è definita a tratti, allora è possibile che nel “punto di incollamento” la funzione abbia una discontinuità.

Tuttavia, in generale non è facile dire quando e come una funzione presenterà una discontinuità: c’è bisogno di fare molta pratica e di avere dimestichezza con lo studio di funzione per poter individuare questi punti con facilità.