Se vogliamo studiare il grafico di una funzione, possiamo procedere con il classico studio di funzione: alla fine del procedimento avremo un grafico qualitativo, che in molti casi è sufficiente per avere un’idea dell’andamento della funzione che stiamo studiando.
Quando lavoriamo con certe funzioni, tuttavia, è bene avere un’idea del loro grafico ben prima di farne lo studio, o addirittura senza neanche doverlo svolgere: stiamo parlando delle cosiddette funzioni elementari.
Funzioni lineari
Le funzioni lineari sono quelle del tipo $$y = ax+b, \qquad a, b \in \mathbb{R}$$Ciascuna di queste funzioni può essere rappresentata come una retta nel piano cartesiano, dove $a$ è il suo coefficiente angolare e $b$ è la sua intercetta.
Potenze con esponente pari
Stiamo parlando delle funzioni della forma $$y = x^p, \qquad p=2n, n \in \mathbb{N}$$La funzione più semplice da analizzare in questa famiglia è la funzione $y=x^2$: questa è una parabola con asse coincidente con l’asse $y$, vertice nell’origine degli assi e concavità rivolta verso l’alto
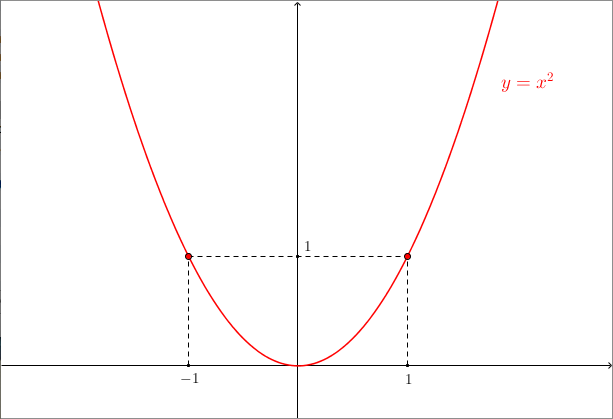
Le altre funzioni sono tutte abbastanza simili a questa parabola:
- il loro grafico sarà un po’ più “schiacciato” verso l’asse $x$ al crescere dell’esponente $p$, se guardiamo tra $-1$ e $1$;
- in corrispondenza di $1$ e $-1$ valgono sempre $1$;
- a sinistra di $-1$ e a destra di $1$ i valori della funzione crescono sempre più rapidamente, all’aumentare di $p$.

Le funzioni con esponente pari sono funzioni pari, cioè con simmetria rispetto all’asse $y$.
Potenze con esponente dispari
Queste sono funzioni del tipo $$y = x^d, \qquad d=2n+1, n \in \mathbb{N}$$A parte la funzione $y=x$, che è la retta bisettrice del primo e del terzo quadrante, la prima funzione che incontriamo è la cubica $y=x^3$:

Le funzioni con esponente più grande sono tutte analoghe a questo “prototipo”, in questo senso:
- il loro grafico sarà un po’ più “schiacciato” verso l’asse $x$ al crescere dell’esponente $d$, se guardiamo tra $-1$ e $1$;
- in corrispondenza di $1$ valgono $1$ e in $-1$ valgono $-1$;
- a sinistra di $-1$ i valori della funzione decrescono, mentre a destra di $1$ i valori della funzione crescono, e lo fanno sempre più rapidamente all’aumentare di $d$.

Notiamo che - come era intuibile - funzioni con esponente dispari sono funzioni dispari, cioè con simmetria centrale rispetto all’origine degli assi.
Potenze con esponente frazionario positivo
Vogliamo studiare le funzioni della forma $$y = x^q, \qquad q \in \mathbb{Q}, q > 0$$Sappiamo che possiamo sempre scrivere $q = \frac{a}{b}$, dove $\frac{a}{b}$ è una frazione ridotta ai minimi termini; possiamo inoltre supporre che $\frac{a}{b}$ non sia un numero naturale, dato che abbiamo già analizzato le funzioni fatte così. Dobbiamo distinguere due casi.
- Se $b$ è pari, la funzione ha come dominio i numeri non negativi. Il grafico è contenuto solo nel primo quadrante.
- Se $b$ è dispari, la funzione ha come dominio tutto $\mathbb{R}$. Bisogna dividere ancora in due casi:
- se $a$ è pari, il grafico della funzione giace nel primo e nel secondo quadrante, e inoltre la funzione è pari;
- se $a$ è dispari, il grafico della funzione giace nel primo e nel terzo quadrante, e inoltre la funzione è dispari.
Le considerazioni appena fatte ci permettono di restringere l’analisi al primo quadrante; per funzioni con $b$ pari avremo studiato la funzione nella sua totalità, mentre per le funzioni con $b$ dispari basterà disegnare la funzione negli altri quadranti tenendo conto delle simmetrie presenti.
Tutte le funzioni di questo tipo passano per l’origine degli assi e per $(1, 1)$. Se $q < 1$, la concavità della funzione nel primo quadrante è rivolta verso il basso, come per le funzioni notevoli radice quadrata e radice cubica. La concavità sarà più accentuata man mano che $q$ si avvicina a $0$.
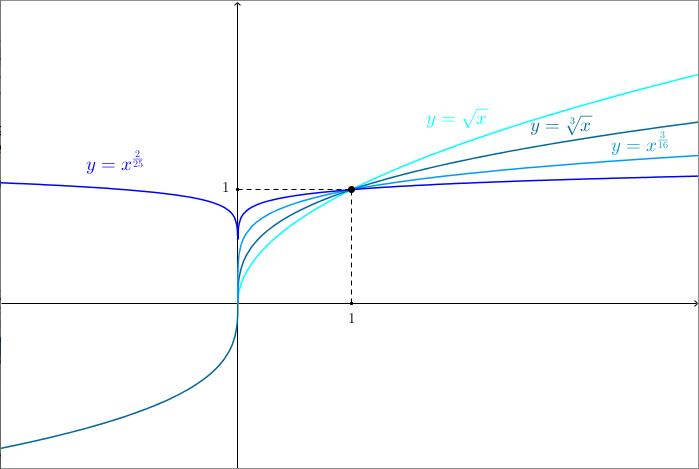
Se $q > 1$ la concavità della funzione nel primo quadrante è rivolta verso l’alto, in maniera del tutto simile a quanto accade per le funzioni a esponente intero. La concavità sarà più accentuata all’aumentare di $q$.

Potenze con esponente pari e negativo
Consideriamo funzioni del tipo $$y = x^{-p}, \qquad p = 2n, n \in \mathbb{N}$$che possiamo riscrivere anche come $$y = \frac{1}{x^p}, \qquad p = 2n, n \in \mathbb{N}$$Le funzioni di questa famiglia sono pari, non sono definite in $x=0$ e hanno un grafico di questo tipo:

Come si vede, all’aumentare di $p$ le funzioni si “schiacciano” sempre di più verso l’asse $x$ a sinistra di $-1$ e a destra di $1$, mentre tra $-1$ e $1$ i valori assunti dalla funzione diventano sempre più grandi (tendendo a $+\infty$ avvicinandoci a $0$).
Potenze con esponente dispari e negativo
Le funzioni del tipo $$y = x^{-d}, \qquad d = 2n+1, n \in \mathbb{N}$$possono essere riscritte come $$y = \frac{1}{x^d}, \qquad d = 2n+1, n \in \mathbb{N}$$Queste funzioni sono dispari e non sono definite in $x=0$. Ecco alcuni grafici:

Come si vede, all’aumentare di $d$ le funzioni si “schiacciano” sempre di più verso l’asse $x$, se guardiamo a sinistra di $-1$ e a destra di $1$; tra $-1$ e $0$ i valori assunti dalla funzione diventano sempre più piccoli, mentre tra $0$ e $1$ sono sempre più grandi (se ci avviciniamo a $0$).
Potenze con esponente frazionario negativo
Per analizzare funzioni della forma $$y=x^{-q} = \frac{1}{x^q}, \qquad q \in \mathbb{Q}, q > 0$$dobbiamo procedere sostanzialmente come per le funzioni con esponente frazionario positivo. Una volta scritto $q = \frac{a}{b}$ con $a, b$ primi fra loro e in modo che $\frac{a}{b}$ non sia un numero naturale, abbiamo una suddivisione in due casi.
- Se $b$ è pari, la funzione ha come dominio i numeri positivi. Il grafico è contenuto solo nel primo quadrante.
- Se $b$ è dispari, la funzione ha come dominio $\mathbb{R}$, escluso lo $0$. Bisogna dividere ancora in due casi:
- se $a$ è pari, il grafico della funzione giace nel primo e nel secondo quadrante, e inoltre la funzione è pari;
- se $a$ è dispari, il grafico della funzione giace nel primo e nel terzo quadrante, e inoltre la funzione è dispari.
Possiamo quindi studiare la funzione solo nel primo quadrante. Tutte le funzioni di questo tipo passano per $(1, 1)$; la concavità della funzione nel primo quadrante è sempre rivolta verso l’alto. Quando $q$ tende a $0$ il grafico della funzione si “avvicina” all’asse $y$, mentre al crescere di $q$ il grafico si “schiaccia” verso l’asse $x$, guardando per ascisse maggiori di $1$.

Funzione esponenziale
Con funzione esponenziale si intende una funzione di questa forma: $$y=a^x, \qquad a \in \mathbb{R}, a > 0$$Possiamo avere due tipologie di grafico, a seconda di quanto vale $a$:
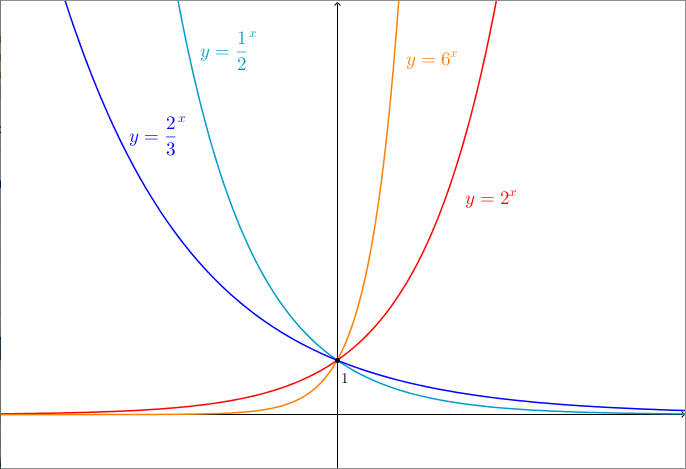
Il grafico passa da $(0, 1)$; quando $a>1$ la funzione è crescente, mentre quando $0 < a < 1$ è decrescente.
Funzione logaritmica
Per funzione logaritmica intendiamo una funzione fatta così: $$y = \log_a x \qquad a \in \mathbb{R}, a > 0$$Abbiamo due tipologie di grafico, in dipendenza da $a$:

Tutti i grafici passano da $(1, 0)$; quando $a > 1$ la funzione è crescente, mentre quando $0 < a < 1$ è decrescente. Sottolineiamo che il dominio di questa funzione, comunque scelta la base del logaritmo, è costituito dai soli numeri reali positivi.
Funzioni trigonometriche
Le funzioni trigonometriche seno, coseno, tangente e cotangente sono definite come rapporti tra i lati di un triangolo rettangolo, ma possono essere definite più in generale grazie all’uso della circonferenza goniometrica. Riportiamo qui i rispettivi grafici:
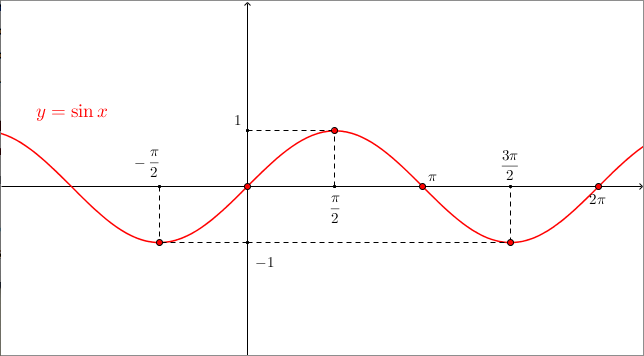
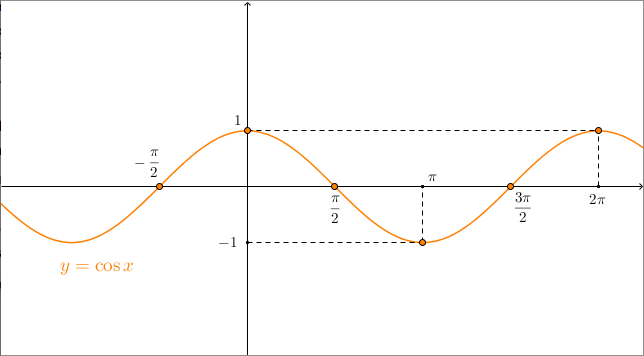


Si nota che queste funzioni sono periodiche: seno e coseno hanno periodo $2\pi$, tangente e cotangente hanno periodo $\pi$.
È possibile anche definire le funzioni trigonometriche inverse: rimandiamo alla lezione dedicata per vedere i loro grafici.
Funzione valore assoluto e funzione segno
La funzione valore assoluto è la funzione definita in questo modo: $$y = \lvert x \rvert = \begin{cases} x & \text{se }x \geq 0 \\ -x & \text{se }x < 0 \end{cases}$$La cosa più importante da notare è che questa funzione assume valori sempre non negativi. Il suo grafico si ottiene “incollando” le rette $y=x$ e $y=-x$ nell’origine (e cancellando le parti in cui il grafico delle rette giace nel terzo e quarto quadrante):

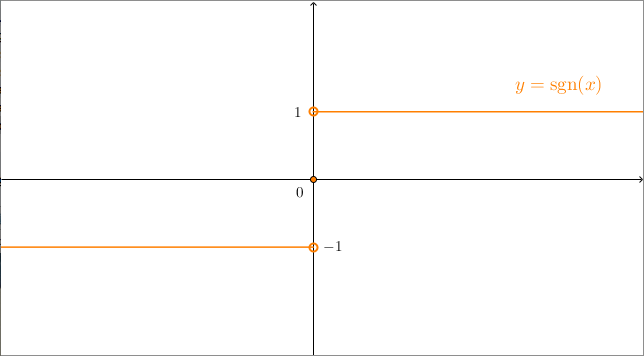
La funzione segno è invece definita così: $$y = \text{sgn}(x) = \begin{cases} 1 & \text{se }x > 0 \\ 0 & \text{se }x = 0 \\ -1 &\text{se } x < 0 \end{cases}$$In poche parole, questa funzione restituisce il segno dell’ascissa in cui viene calcolata (e vale $0$ in $0$, dato che $0$ non ha segno). È una funzione non continua, dato che in $0$ c’è una discontinuità di prima specie.
Tra le altre funzioni elementari che vale la pena di ricordare ci sono anche le funzioni iperboliche, a cui abbiamo dedicato un articolo a sé stante.