La circonferenza goniometrica è uno strumento molto utile nello studio della trigonometria, che permette di visualizzare i valori che assumono le funzioni trigonometriche calcolate in qualunque angolo. Essa stabilisce un legame fondamentale tra geometria analitica e trigonometria.
La circonferenza goniometrica è una circonferenza con centro nell’origine $\mathcal{O}$ del piano cartesiano, di raggio $1$. Per questo motivo a volte è detta anche circonferenza unitaria.

Chiamiamo $\Gamma$ questa circonferenza: come sappiamo dalla geometria analitica, l’equazione che la descrive, in coordinate cartesiane, è$$ \Gamma: \quad x^2 + y^2 =1 $$Ora consideriamo un punto $P$ appartenente alla circonferenza $\Gamma$, e tracciamo la semiretta passante per $\mathcal{O}$ e $P$ di origine $\mathcal{O}$; inoltre, consideriamo la semiretta costituita dal semiasse delle ascisse contrassegnato dalle ascisse positive, ossia l’insieme descritto analiticamente come $\{ (x, y) \in \mathbb{R}^2 \ |\ x \geq 0 \ \}$. Chiamiamo $\alpha = \alpha (P)$ l’angolo che si ottiene facendo sovrapporre il semiasse positivo delle $x$ con la semiretta passante per $P$, come illustrato nella seguente figura:

Quel che vogliamo mostrare è che, comunque venga scelto il punto $P \in \Gamma$, sussiste una relazione fondamentale tra le sue coordinate, $x_P$ e $y_P$, e il valore delle funzioni trigonometriche seno e coseno, calcolate nell’angolo $\alpha$, cioè con $\sin(\alpha)$ e $\cos(\alpha)$.
Tutte le costruzioni successive suppongono che $P$ si trovi in una posizione “generica”, ovvero, non si trovi nelle quattro intersezioni degli assi cartesiani con la circonferenza $\Gamma$: se così fosse, alcuni enti da noi descritti in seguito non esisterebbero nemmeno! Questi casi verranno trattati in seguito, quando avremo più dimestichezza con la circonferenza unitaria.
Costruiamo ora il segmento perpendicolare all’asse $x$ che passa per $P$, che incontra l’asse delle ascisse nel punto $H$, e consideriamo il triangolo $\mathcal{O}PH$, rettangolo in $H$ per costruzione:

L’ipotenusa di questo triangolo è il segmento $\mathcal{O} P $, che congiunge il centro della circonferenza $\Gamma$ con un punto giacente su di essa: la sua misura è dunque quella del raggio, $1$.
Limitiamoci per un momento all’ipotesi che l’angolo $\alpha$ sia un angolo acuto, nel caso in cui, cioè, il punto $P$ si trovi nel primo quadrante. In questo caso, l’angolo $\alpha$ viene a coincidere con l’angolo $\widehat{H\mathcal{O}P}$: allora possiamo calcolare la misura dei cateti $PH$ e $\mathcal{O}H$ del triangolo $\mathcal{O}PH$ mediante la definizione del seno e del coseno di un angolo all’interno di un triangolo rettangolo: ##KATEX##\begin{aligned} \sin(\widehat{H\mathcal{O}P}) = \frac{PH}{P\mathcal{O}} & \quad \Rightarrow \quad PH = \sin(\widehat{H\mathcal{O}P}) \cdot P\mathcal{O} \\ \cos(\widehat{H\mathcal{O}P}) = \frac{\mathcal{O}H}{P\mathcal{O}} & \quad \Rightarrow \quad \mathcal{O}H = \cos(\widehat{H\mathcal{O}P}) \cdot P\mathcal{O} \end{aligned}##KATEX##Ricordando però che l’ipotenusa $P\mathcal{O}$ misura $1$, otteniamo che ##KATEX##\begin{aligned} \sin(\widehat{H\mathcal{O}P}) = PH \\ \cos(\widehat{H\mathcal{O}P}) = \mathcal{O}H \end{aligned}##KATEX##
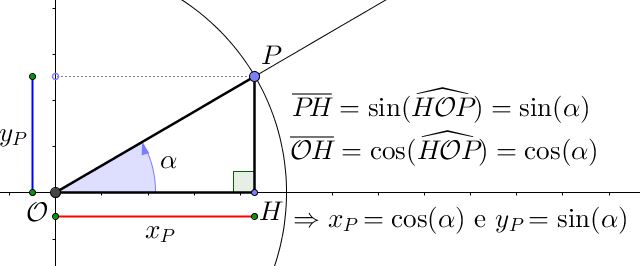
Il significato dei due cateti è presto detto: se $x_P$ e $y_P$ sono le coordinate del punto $P$, si ha che $x_P = \mathcal{O}H$ e $y_P = PH$. Possiamo quindi concludere che, almeno in questo caso, le coordinate del punto $P$ coincidono, rispettivamente, con coseno e seno dell’angolo $\alpha$ individuato dalla semiretta passante per $P$.
Ora generalizziamo queste considerazioni, rimuovendo l’ipotesi che $P$ si trovi nel primo quadrante. Notiamo innanzitutto che, tra il segno delle coordinate di $P$ e l’angolo $\alpha$ valgono le seguenti relazioni: $$ \begin{cases} P \in \text{ I quadrante } & \Leftrightarrow & 0 \leq \alpha \leq \frac{\pi}{2} & \Leftrightarrow & x_P \geq 0 \text{ e } y_P \geq 0 \\ P \in \text{ II quadrante } & \Leftrightarrow & \frac{\pi}{2} \leq \alpha \leq \pi & \Leftrightarrow & x_P \leq 0 \text{ e } y_P \geq 0 \\ P \in \text{ III quadrante } & \Leftrightarrow & \pi \leq \alpha \leq \frac{3 \pi}{2} & \Leftrightarrow & x_P \leq 0 \text{ e } y_P \leq 0 \\ P \in \text{ IV quadrante } & \Leftrightarrow & \frac{3 \pi}{2} \leq \alpha \leq 2 \pi & \Leftrightarrow & x_P \geq 0 \text{ e } y_P \leq 0 \end{cases} $$

Ci approntiamo ad illustrare che, indipendentemente dal quadrante in cui si trova il punto $P$, le sue coordinate rispettano sempre le relazioni$$ \boxed{\begin{cases} x_P = \cos (\alpha) \\ y_P = \sin (\alpha) \end{cases}} $$
Consideriamo dapprima il caso in cui $P$ si trovi nel secondo quadrante, caratterizzato da quindi da ordinata positiva e ascissa negativa, mentre l’angolo $\alpha$ sarà compreso tra $\frac{\pi}{2}$ e $\pi$. Date queste ipotesi, è possibile costruire due cose:
- innanzitutto, il punto $P’$, che abbia la stessa ordinata di $P$, ma l’ascissa di segno opposto (cioè positivo): $$ \begin{cases} x_{P’} = - x_P \\ y_{P’} = y_P \end{cases} $$In pratica, si tratta di riportare il punto $P$ nel primo quadrante. Dopo aver costruito $P’$, possiamo proiettarlo sull’asse delle $x$ ottenendo il punto $H’$.
- In secondo luogo, è possibile trovare l’angolo $\beta$, supplementare ad $\alpha$, cioè quell’angolo che, sommato ad $\alpha$ produce un angolo piatto; per quanto detto su $\alpha$, $\beta$ deve essere acuto (o al massimo retto): difatti, se $\alpha + \beta = \pi$, segue che $\beta = \pi - \alpha$, e quindi, sapendo che $\frac{\pi}{2} \leq \alpha \leq \pi$, otteniamo che $0 \leq \beta \leq \frac{\pi}{2}$. Inoltre, quest’angolo è proprio l’angolo $\widehat{H\mathcal{O}P}$.
Se la costruzione sembra complicata, si faccia riferimento alla figura seguente:

Ora prendiamo in esame, sempre con riferimento alla figura precedente, il triangolo $\mathcal{O}P’H’$. Notiamo che esso è rettangolo in $H’$ per costruzione, e, sempre per costruzione, i cateti $P’H’$ e $\mathcal{O}H’$ sono rispettivamente congruenti ai cateti $PH$ e e $\mathcal{O}H$ del triangolo $\mathcal{O}PH$. Nell’illustrazione abbiamo evidenziato con colori uguali cateti congruenti, per evitare confusione. Concludiamo che, per il primo criterio di congruenza, i triangoli $\mathcal{O}PH$ e $\mathcal{O}P’H’$ sono congruenti: di conseguenza, anche gli angoli $\widehat{H\mathcal{O}P}$ e $\widehat{H’\mathcal{O}P’}$ sono congruenti (sono segnati in verde nel disegno), e misurano entrambi $\beta = \pi - \alpha$.
Concentriamo la nostra attenzione su $P’$: è un punto nel primo quadrante, e il triangolo $\mathcal{O}P’H’$ è del tutto analogo a quello che abbiamo costruito in precedenza, quando il punto $P$ si trovava, per l’appunto, nel primo quadrante: allora le coordinate del punto $P’$ soddisfano a questo sistema $$ \begin{cases} x_{P’} = \cos(\beta) \\ y_{P’} = \sin(\beta) \end{cases} $$ma sostituendo nel precedente sistema l’espressione delle coordinate di $P$ in funzione di quelle di $P’$, e l’espressione trovata per il valore di $\beta$, otteniamo$$ \begin{cases} -x_{P} = \cos(\pi - \alpha) \\ y_{P} = \sin(\pi - \alpha) \end{cases} $$ora sfruttiamo le espressioni di seno e coseno di angoli associati per arrivare ad eliminare questo fastidioso “$\pi -$” dalle precedenti equazioni, mettendo in evidenza l’angolo $\alpha$: si ha che $\sin(\pi - \alpha) = \sin(\alpha)$ e che $\cos(\pi - \alpha) = - \cos (\alpha)$. Dunque, riscrivendo le funzioni trigonometriche nel sistema precedente, arriviamo a $$\begin{cases} -x_{P} = -\cos(\alpha) \\ y_{P} = \sin(\alpha)\end{cases} \quad \Rightarrow \quad \begin{cases} x_{P} = \cos(\alpha) \\ y_{P} = \sin(\alpha)\end{cases}$$che è quel che volevamo ottenere.
È chiaro che questo ragionamento si può attuare anche quando $P$ si trova nel terzo o nel quarto quadrante: sfruttando la medesima costruzione, cioè di riportare $P$ nel primo quadrante e di costruire un triangolo rettangolo congruente a $\mathcal{O}PH$, usando le relazioni che regolano i valori che le funzioni trigonometriche assumono su angoli associati, per raggiungere sempre lo stesso risultato: $$ \begin{cases} x_P = \cos (\alpha) \\ y_P = \sin(\alpha) \end{cases}$$

Queste formule valgono anche nei casi speciali in cui $P$ si trovi su una delle quattro intersezioni della circonferenza unitaria $\Gamma$ con gli assi coordinati: infatti, queste posizioni individuano gli angoli orientati a $\frac{\pi}{2}$, $\pi$, $\frac{3 \pi}{2}$ e $2 \pi$. Ricordando i valori di seno e coseno in questi angoli notevoli, ci accorgiamo che anche in questi casi le relazioni $x_P = \cos (\alpha)$ e $y_P = \sin (\alpha)$ continuano a valere:

Quindi possiamo concludere che ogni punto della circonferenza goniometrica identifica un angolo compreso tra $0$ e $2 \pi$, e le coordinate di quel punto sono i valori che le funzioni trigonometriche assumono calcolate in quell’angolo: abbastanza comodo, se non si possiede una calcolatrice scientifica. Ma anche senza possedere un compasso e una riga graduata, possiamo sfruttare questa corrispondenza tra coordinate e valori delle fuznioni goniometriche per ricavare facilmente il segno di quest’ultime.
Inoltre, la circonferenza goniometrica rende conto della periodicità di $2 \pi$ delle funzioni seno e coseno. Per quanto riguarda le funzioni, infatti, sappiamo che $\sin(\alpha) = \sin(\alpha + 2 \pi)$ $= \sin(\alpha + 4 \pi)$ $= \dots = \sin(\alpha + 2 k \pi)$ e che, similmente, $\cos(\alpha) = \cos(\alpha + 2 k \pi)$. Aggiungere o togliere uno o più angoli di $2 \pi$ radianti ad un angolo individuato sulla circonferenza goniometrica, non a caso detto “angolo giro”, significa compiere un intero giro sulla circonferenza, in senso antiorario se si aggiunge $2 \pi$, orario se si sottrae:
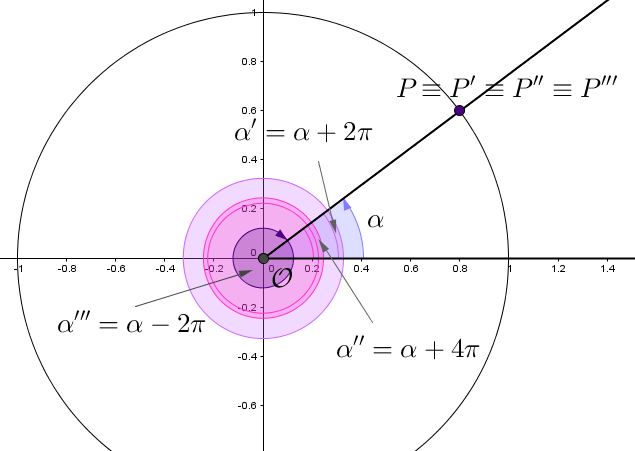
Ma c’è di più: seno e coseno non sono le uniche funzioni trigonometriche che si possono scovare disegnate nella circonferenza goniometrica: ci sono tutte le altre, dalla tangente alla cosecante!
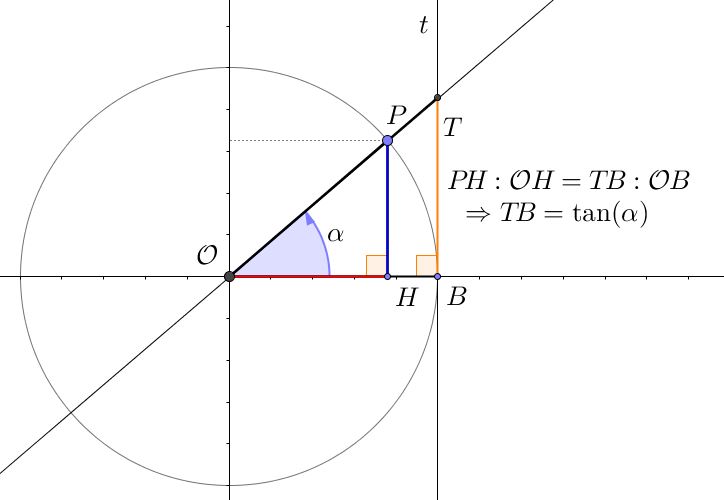
A titolo d’esempio, illustriamo come ottenere un segmento che misuri la tangente di un angolo. Data la nostra circonferenza trigonometrica $\Gamma$, conduciamo la retta $t$ tangete alla circonferenza nel suo punto $B$ di coordinate $(1;0)$. Ancora una volta, si abbia l’accortezza di non scegliere $P$ in una posizione particolare, e iniziamo il ragionamento prendendolo: con questo accorgimento, la retta passante per $\mathcal{O}$ e $P$ ha sicuramente intersezione con $t$, diversa da $B$: chiamiamo $T$ questo punto di intersezione. Ora dimostriamo che il segmento $TB$ misura proprio $\tan(\alpha)$!
Per far questo, consideriamo i triangoli $\mathcal{O}PH$ e $\mathcal{O}BT$. Essi hanno un angolo in comune, $\alpha$, ed entrambi un angolo retto (rispettivamente, $\widehat{\mathcal{O}HP}$ e $\widehat{\mathcal{O}BT}$): sono dunque triangoli simili. Sussite quindi la proporzione $PH : \mathcal{O}H = TB : \mathcal{O}B$. Lo stesso risultato si può ottenere mediante il teorema di Talete. Nella proporzione sostituiamo le equivalenze, mostrate in precedenza, secondo cui $PH = \sin(\alpha)$ e $\mathcal{O}H = \cos(\alpha)$; inoltre, essendo $B$ appartenente a $\Gamma$, $\mathcal{O}B$ misura quanto il raggio, $1$: tenuto conto di tutto questo, si ottiene $$ \sin(\alpha) : \cos(\alpha) = TB : 1 \ \Rightarrow \ TB = \sin(\alpha) : \cos(\alpha) $$Ma ricordiamo la identità che definisce la tangente di un angolo: $ \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}$, possiamo concludere che, nel caso in cui $P$ si trovi nel primo quadrante, e non in posizioni particolari (cioè $0 < \alpha < \frac{\pi}{2}$), vale l’uguaglianza $$ TB = \tan(\alpha) $$
L’uguaglianza si può dimostrare, prestando attenzione ai segni, anche nel caso in cui $P$ sia negli altri quadranti: nel caso in cui $P$ venga a trovarsi nel secondo o nel quarto quadrante, infatti, la tangente dell’angolo $\alpha$ risulta essere negativa; il segmento $TB$, in quanto segmento, non può misurare una quantità negativa: questa discrepanza di segno è individuata dal fatto che, in questo caso, il punto $T$ abbia un’ordinata negativa. Sarebbe infatti più corretto dire che il segmento $BT$ misura $| \tan(\alpha) |$, e che l’ordinata del punto $T$ è proprio (tenuto conto del segno) $\tan(\alpha)$. Facciamo notare come il nome stesso della tangente sia collegato ad un segmento staccato sulla retta tangete alla circonferenza unitaria.
La costruzione appena svolta mette in luce parecchi aspetti della funzione trigonometrica $\tan(x)$:
- Il periodo di $\pi$ radianti invece che di $2\pi$ radianti, tipico delle funzioni seno e coseno. Dato l’angolo $\alpha$, consideriamo un angolo di $\alpha + \pi$, cioè spostiamoci in senso antiorario di mezzo giro sulla circonferenza goniomentrica. Ad $\alpha + \pi$ corrisponde il punto $P’$, evidenziato sulla circonferenza goniometrica nell’illustrazione sottostante: il punto $T$ che si trova svolgendo la costruizione descritta prima, per entrambi i punti $P$ e $P’$, ossia per gli angoli $\alpha$ e $\alpha + \pi$, è il medesimo. Questo non deve stupire, dato che i punti $P$, $\mathcal{O}$ e $P’$ risultano allineati, e dunque la retta passante per $P$ e $\mathcal{O}$ è la stessa retta che passa per $P’$ e $\mathcal{O}$.
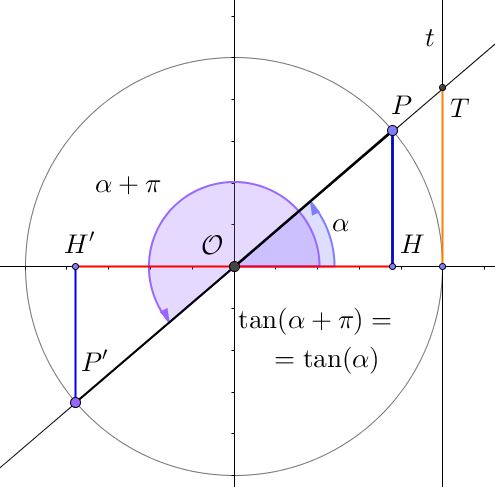
- Man mano che l’angolo $\alpha$ si avvicina a $0$ radianti, cioè che il punto $P$ si avvicina a $(1;0)$, il punto $T$ va a coincidere con $B$ (e con $H$), e dunque ci accorgiamo che la tangente di un angolo di $0$ radianti misura proprio $0$. Lo stesso accade se $P$ si avvicina a $(-1;0)$, o equivalentemente se $\alpha$ tende a $\pi$.
- Se invece $P$ si trovasse in $(0;1)$, in corrispondenza cioè di un angolo di $\frac{\pi}{2}$ radianti, la retta passante per $P$ e $\mathcal{O}$ sarebbe parallela alla retta $t$: il punto $T$ non esisterebbe nemmeno! Lo stesso accade se $P$ è il punto $(0;-1)$. Questo rende conto del fatto che il dominio della funzione tangente non comprende i punti del tipo $\frac{\pi}{2} + k \pi$, con $k$ numero intero.
- Inoltre, possiamo avere un’intuizione grafica dei limiti della funzione tangente, quando il suo argomento si avvicina ai valori “proibiti”: ad esempio, facendo avvicinare $P$ a $(0;1)$, cioè facendo tendere $\alpha$ a $\frac{\pi}{2}$, si vede bene come l’ordinata del punto $T$ si sposti verso un valore infinitamente alto o infinitamente basso:


Questo rende conto del limite $\displaystyle{\lim_{x \to {\frac{\pi}{2}}^\pm} \tan (x) = \pm \infty}$.
La seguente illustrazione mette in evidenza altri segmenti notevoli che possono essere individuati sulla circonferenza goniometrica: si possono disegnare segmenti che misurano, oltre che seno, coseno e tangente, la cotangente, la secante e la cosecante di un angolo.
