Nell’ambito della trigonometria, storicamente, è stato scelto di dare un nome anche alle funzioni reciproche di seno e coseno: esse si chiamano rispettivamente cosecante e secante. Nella pratica, molto spesso, queste funzioni non vengono nemmeno menzionate, dato che possono essere definite a partire dalle funzioni trigonometriche di base; è comunque bene conoscere le loro proprietà e fare un po’ di pratica per sapere come utilizzarle.
Definizione
Chiamiamo secante la seguente funzione: ##KATEX##\begin{aligned} \sec: \mathbb{R} & \rightarrow \mathbb{R} \\ x & \mapsto \sec(x):=\frac{1}{\cos(x)}\end{aligned}##KATEX##Questa funzione associa quindi a un numero reale $x$ il reciproco del coseno di $x$. Ecco il suo grafico:

Si chiama invece cosecante la seguente funzione: ##KATEX##\begin{aligned} \csc: \mathbb{R} & \rightarrow \mathbb{R} \\ x & \mapsto \csc(x):=\frac{1}{\sin(x)}\end{aligned}##KATEX##La cosecante associa quindi a un numero reale $x$ il reciproco del seno di $x$. Disegniamone il grafico:
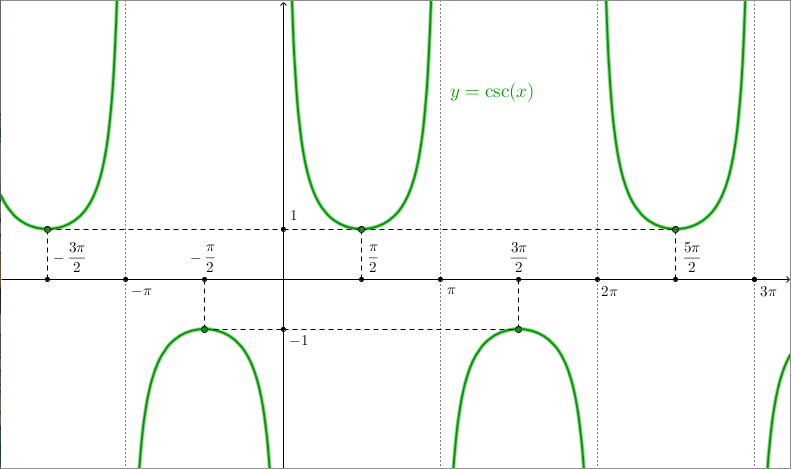
Guardando il grafico delle funzioni a la loro definizione possiamo fare alcune osservazioni.
- La secante ha dominio $$D_{\sec}: \left \{ x \in \mathbb{R} \ \vert \ x \neq \frac{\pi}{2} + k\pi, \ k \in \mathbb{Z} \right \}$$mentre la cosecante ha dominio $$D_{\csc}: \{ x \in \mathbb{R} \ \vert \ x \neq k\pi, \ k \in \mathbb{Z} \}$$
- Secante e cosecante sono periodiche di periodo $2 \pi$, dato che coseno e seno lo sono. Inoltre, la secante è anche una funzione pari.
- Grazie a queste funzioni possiamo definire le funzioni tangente e cotangente in un altro modo: $$\tan(x) = \sin(x) \cdot \sec(x) \qquad \cot(x) = \cos(x) \cdot \csc(x)$$
- Utilizzando sistematicamente la formula di derivazione del reciproco di una funzione, possiamo calcolare le derivate di secante e cosecante: ##KATEX##\begin{aligned} (\sec (x) )’ & = \left ( \frac{1}{\cos(x)} \right )’ = \frac{-\sin(x)}{\cos^2(x)} = - \tan(x)\sec(x) \\ (\csc (x) )’ & = \left ( \frac{1}{\sin(x)} \right )’ = \frac{\cos(x)}{\sin^2(x)} = - \cot(x)\csc(x) \end{aligned}##KATEX##È possibile anche ricavare una formula per l’integrale indefinito di queste funzioni: ##KATEX##\begin{aligned} \int \sec(x)dx & = \ln \left | \tan \left ( \frac{x}{2} + \frac{\pi}{4} \right ) \right | + C \\ \int \csc(x)dx & = \ln \left | \cot \left ( \frac{x}{2} \right ) \right | + C \end{aligned}##KATEX##
- A partire da secante e cosecante possiamo formulare una “nuova versione” dell’identità trigonometrica fondamentale (che è valida solamente all’interno dei domini di secante e cosecante): $$\csc^2(x) + \sec^2(x) = \csc^2(x) \sec^2(x)$$
È possibile anche dare un’interpretazione geometrica della secante e cosecante di un numero reale, interpretando questo numero come l’ampiezza di un angolo.
- Se l’angolo di cui stiamo parlando è interno a un triangolo rettangolo, allora la secante è il rapporto tra l’ipotenusa e il cateto adiacente all’angolo; la cosecante è invece il rapporto tra l’ipotenusa e il cateto opposto.
- Se l’angolo è invece considerato sulla circonferenza goniometrica, secante e cosecante possono essere interpretate come la lunghezza di particolari segmenti:
