L’equazione $x^2 + y^2 = 1$, nel piano cartesiano, descrive il luogo dei punti distanti $1$ dall’origine degli assi: è la circonferenza unitaria centrata nell’origine. In trigonometria, questa circonferenza viene chiamata circonferenza goniometrica e in questo contesto si mostra che le coordinate di ciascun punto della circonferenza possono essere scritte come $(\cos(t), \sin(t))$, dove $t$ è un opportuno angolo. Questo quindi ci dice che possiamo descrivere la circonferenza come curva parametrica: le coordinate dei punti della curva variano in dipendenza di un certo parametro - $t$, appunto - che può essere interpretato geometricamente come la misura dell'ampiezza di un angolo.
Invece, l’equazione $x^2 - y^2 = 1$ descrive un luogo di punti di tutt’altro genere: è l’iperbole equilatera con asintoti $y = \pm x$ e fuochi $F_{1, 2} = (\pm \sqrt{2}, 0)$. Ci chiediamo: è possibile parametrizzare questa curva in maniera simile a quanto abbiamo fatto per la circonferenza?
Definizione
Chiamiamo coseno iperbolico la funzione così definita: ##KATEX##\begin{aligned} \cosh : \mathbb{R} & \rightarrow \mathbb{R} \\ t & \mapsto \cosh(t) : = \frac{e^t + e^{-t}}{2} \end{aligned}##KATEX##

Invece, chiamiamo seno iperbolico la seguente funzione: ##KATEX##\begin{aligned} \sinh : \mathbb{R} & \rightarrow \mathbb{R} \\ t & \mapsto \sinh(t) : = \frac{e^t - e^{-t}}{2} \end{aligned}##KATEX##

Queste funzioni, dette funzioni iperboliche, costituiscono una possibile parametrizzazione dell’iperbole equilatera. Più precisamente, i punti del ramo di destra dell’iperbole $x^2 - y^2 = 1$ possono essere descritti così: $$P_{h^+}(t) = ( \cosh(t), \sinh(t) ), \qquad t \in \mathbb{R}$$I punti del ramo di sinistra invece hanno questa descrizione: $$P_{h^-}(t) = ( -\cosh(t), \sinh(t) ), \qquad t \in \mathbb{R}$$

Come mai queste funzioni vanno bene per parametrizzare l’iperbole? Semplicemente perché, per qualsiasi $t$ scelto, vale la seguente identità fondamentale delle funzioni iperboliche: $$\cosh^2(t) - \sinh^2(t) = 1$$Infatti ##KATEX##\begin{aligned} \cosh^2(t) - \sinh^2(t) & = \left ( \frac{e^t + e^{-t}}{2} \right )^2 - \left ( \frac{e^t - e^{-t}}{2} \right )^2 = \\ & = \frac{e^{2t} + 2 e^t \cdot e^{-t} + e^{-2t}}{4} - \frac{e^{2t} - 2 e^t \cdot e^{-t} + e^{-2t}}{4} = \\ & = \frac{4}{4} = 1 \end{aligned}##KATEX##
Definizione
La tangente iperbolica è la funzione definita come il rapporto tra seno e coseno iperbolico: ##KATEX##\begin{aligned} \tanh: \mathbb{R} & \rightarrow \mathbb{R} \\ t & \mapsto \tanh(t) := \frac{\sinh(t)}{\cosh(t)} = \frac{e^t - e^{-t}}{e^t + e^{-t}} \end{aligned}##KATEX##
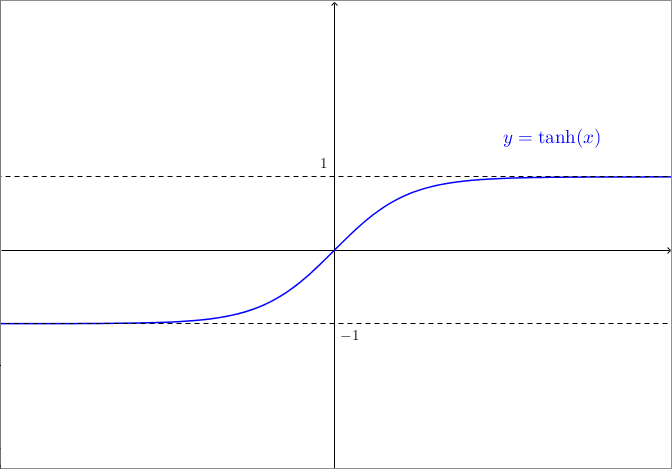
La cotangente iperbolica è invece il rapporto tra coseno e seno iperbolico: ##KATEX##\begin{aligned} \coth: \mathbb{R} & \rightarrow \mathbb{R} \\ t & \mapsto \coth(t) := \frac{\cosh(t)}{\sinh(t)} = \frac{e^t + e^{-t}}{e^t - e^{-t}} \end{aligned}##KATEX##

Segnaliamo inoltre che è possibile definire - in maniera ovvia - un analogo della secante e della cosecante: la secante iperbolica e la cosecante iperbolica.
Proprietà delle funzioni iperboliche
Ecco le principali caratteristiche delle funzioni iperboliche.
| $y = \sinh(x)$ | $y = \cosh(x)$ | $y = \tanh(x)$ | $y = \coth(x)$ | |
| Dominio | $\mathbb{R}$ | $\mathbb{R}$ | $\mathbb{R}$ | $(-\infty, 0) \cup (0, +\infty)$ |
| Codominio | $\mathbb{R}$ | $[1, +\infty)$ | $[-1, 1]$ | $(-\infty, -1) \cup (1, +\infty)$ |
| Derivata | $\cosh(x)$ | $\sinh(x)$ | $1 - \tanh^2(x)$ | $1 - \coth^2(x)$ |
| Primitiva | $\cosh(x)$ | $\sinh(x)$ | $\ln ( \cosh(x))$ | $\ln(\sinh(x))$ |
| Parità | Dispari | Pari | Dispari | Dispari |
Il parallelismo con le funzioni trigonometriche è evidente in molte delle caratteristiche delle funzioni iperboliche. Le analogie vanno ben oltre, dato che vale questo sorprendente risultato:
Regola di Osborn. Prendiamo una qualsiasi identità trigonometrica. Svolgiamo il seguente procedimento:
- riscriviamo l’identità in termini delle funzioni $\sin(x)$ e $\cos(x)$;
- al posto di $\sin(x)$ scriviamo $\sinh(x)$ e al posto di $\cos(x)$ scriviamo $\cosh(x)$;
- ogni volta che compare $\sinh^2(x)$ aggiungiamo un segno meno davanti al termine in cui è presente.
L’identità ottenuta dopo questo procedimento è ancora valida.
Per capire meglio quanto detto, facciamo un esempio pratico. Prendiamo la formula di duplicazione della tangente: $$\tan(2 \alpha) = \frac{\tan \alpha}{1-\tan^2\alpha}$$Seguiamo passo per passo la regola di Osborn.
- Scriviamo l’identità esplicitando le funzioni seno e coseno: $$\frac{\sin(2 \alpha)}{\cos(2 \alpha)} = \frac{\frac{\sin \alpha}{\cos \alpha}}{1- \frac{\sin^2 \alpha}{\cos^2 \alpha} }$$
- Rimpiazziamo le funzioni trigonometriche con le funzioni iperboliche: $$\frac{\sinh(2 \alpha)}{\cosh(2 \alpha)} = \frac{\frac{\sinh \alpha}{\cosh \alpha}}{1- \frac{\sinh^2 \alpha}{\cosh^2 \alpha} }$$
- Mettiamo un segno $-$ davanti a tutte le espressioni che contengono $\sinh^2 \alpha$ (solo una nel nostro caso): $$\frac{\sinh(2 \alpha)}{\cosh(2 \alpha)} = \frac{\frac{\sinh \alpha}{\cosh \alpha}}{1- \left ( - \frac{\sinh^2 \alpha}{\cosh^2 \alpha} \right )}$$
La nuova identità, che potremmo chiamare “formula di duplicazione della tangente iperbolica”, può essere riscritta così: $$\tanh(2 \alpha) = \frac{\tanh \alpha}{1+\tanh^2\alpha}$$
Alcune curiosità sulle funzioni iperboliche
- Le funzioni iperboliche $\sinh(x)$ e $\cosh(x)$ sono soluzioni dell’equazione differenziale $y’’ = y$ (insieme ad altre opportune combinazioni lineari di $e^x$ ed $e^{-x}$).
- Consideriamo una corda che abbia le estremità appese e fissate, che risenta solamente del suo peso (cioè dell’azione della forza di gravità su di essa). È possibile mostrare che la forma che assume la corda in questa situazione è il grafico di $\cosh(x)$, opportunamente traslato e riscalato. Tale curva si chiama catenaria.
- Grazie alla formula di Eulero è possibile mostrare la validità delle seguenti identità: ##KATEX##\begin{aligned} \sinh(ix) & = -i \sin (x) \\ \cosh(ix) & = \cos(x) \end{aligned}##KATEX##La lettera $i$ rappresenta l’unità immaginaria dei numeri complessi.