La leva è uno degli esempi più comuni di macchina meccanica semplice: serve a trasformare (o meglio a trasferire) energia cinetica. Essa è costituita da un corpo rigido, appunto la leva, capace di ruotare attorno ad un suo punto fisso, detto fulcro. Tipicamente, su una leva agisce una forza, detta forza resistente o resistenza che noi intendiamo vincere o controbilanciare con una nostra azione, la quale può essere applicata in un punto particolare della leva. Ricordiamo infatti che le forze sono grandezze vettoriali e, in quanto tali, caratterizzate anche da un punto di applicazione.
In base alle posizioni reciproche di questi tre punti, cioè il fulcro, il punto di applicazione della nostra forza e il punto dove si trova la resistenza, le leve possono essere classificate in tre generi.
- Primo genere: il fulcro si trova tra il punto in cui noi possiamo applicare la forza e il punto in cui si trova la forza resistente.

Un paio di forbici o un’altalena costituiscono un buon esempio di leva di primo genere. - Secondo genere: il punto in cui si trova la forza resistente si trova fra il fulcro e il punto in cui noi applichiamo la forza.

Un esempio di leva di secondo genere può essere una carriola impugnata per i manici o uno schiaccianoci. - Terzo genere: si applica la forza in un punto più vicino al fulcro di quanto non sia il punto in cui è situata la forza resistente.
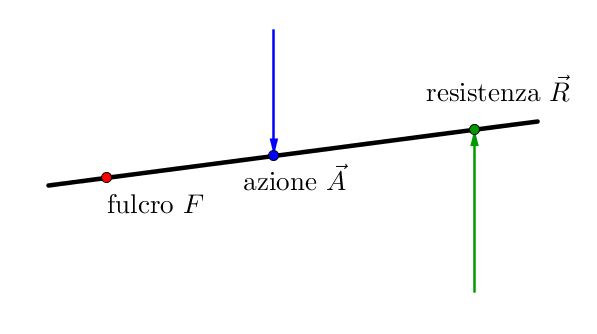
Quando si scava il terreno con un badile o si solleva qualcosa con la mano, usando i muscoli del nostro braccio, si utilizza una leva di terzo genere.
Il principio secondo il quale funzionano tutti i generi di leva è uno solo: si tratta dell’equilibrio dei momenti meccanici applicati al corpo rigido che costituisce la leva.
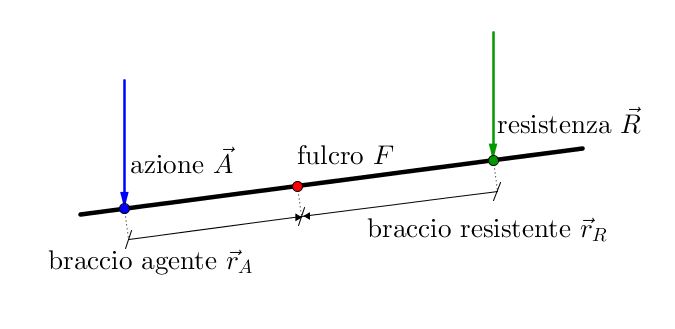
Detta $\vec{A}$ la forza da noi applicata alla leva ed $\vec{R}$ la forza resistente, calcoliamo i momenti di queste due forze, rispetto allo stesso polo: il fulcro. Chiamiamo $F$ il fulcro, $P_A$ il punto in cui applichiamo $\vec{A}$ e $P_R$ il punto in cui si trova la forza resistente $\vec{R}$, e conseguentemente definiamo i bracci d’azione $\vec{r}_A = \overrightarrow{FP_A}$ e resistente $\vec{r}_R = \overrightarrow{FP_R}$: a questo punto, i momenti da trovare sono $\vec{M}_A = \vec{r}_A \times \vec{A}$ e $\vec{M}_R = \vec{r}_R \times \vec{R}$.

Ora suppponiamo che la resistenza e la forza vengano applicate in direzione ortogonale alla leva, di modo che il modulo dei due momenti si calcoli semplicemente mediante il prodotto della lunghezza del braccio per il modulo della forza (in accordo con quanto prescritto dalle regole del prodotto vettore). Con questa ulteriore precisazione, possiamo trovare la condizione di equilibrio di una leva: si ha equilibrio meccanico quando i due momenti, agente e resistente, si equivalgono $$ r_A \cdot A = r_R \cdot R$$
Un’ulteriore classificazione delle leve può avvenire al confronto fra le forze in gioco: se il modulo della forza da noi applicata è maggiore del modulo della resistenza, cioè se $| \vec{A} | > |\vec{R}|$ allora la leva si dice svantaggiosa; viceversa se la forza da applicare per vincere la resistenza è inferiore a quest’ultima, cioè se $| \vec{A} | < | \vec{R} |$, la leva si dice vantaggiosa; infine se i moduli di forza e resistenza si equivalgono ($|\vec{A}| = |\vec{R}|$), la leva si dice indifferente.
In base ai bracci che costituiscono una leva, possiamo stabilire subito se essa sia vantaggiosa o svantaggiosa: dall’equilibrio dei momenti $ r_A \cdot A = r_R \cdot R$ in infatti deduciamo che $ A = \frac{r_R}{r_A} \cdot R$, e dunque a seconda del rapporto $\frac{r_R}{r_A}$ tra il braccio resistente ed il braccio d’azione posssiamo riconoscere leve sicuramente vantaggiose o svantaggiose:
- Nelle leve di secondo genere, il punto di applicazione della nostra azione è più distante dal fulcro del punto in cui si trova la forza resistente: quindi sicuramente è $r_A > r_R \Rightarrow$ $\frac{r_A}{r_R} > 1$ $\Rightarrow \frac{r_R}{r_A} < 1$ $\Rightarrow A < R$; di conseguenza tutte le leve di secondo genere sono vantaggiose.
- Al contrario, le leve di secondo genere sono caratterizzate dal fatto che il fulcro è più distante dalla resistenza di quanto non lo sia dal punto di applicazione della forza d’azione: deve allora valere la disuguaglianza $r_A < r_R$, e dunque, seguendo lo stesso ragionamento del punto precedente, sarà sempre $A > R$: tutte le leve di terzo genere sono svantaggiose.
- Nelle leve di primo genere, a priori non possiamo dire nulla: si possono presentare entrambe le situazioni: se il braccio agente è più corto del braccio resistente ($r_A < r_R$) avremo una leva svantaggiosa, viceversa se il braccio resistente è più corto del braccio agente ($r_R < r_A$) la leva è vantaggiosa. Se infine i bracci sono lunghi uguali, la leva è indifferente.