Nella meccanica, per descrivere il moto dei corpi, si è fatto spesso riferimento al punto materiale: un punto geometrico, privo di dimensione, ma dotato di massa. Questa è ovviamente un’approssimazione del mondo che ci circonda: i corpi hanno delle dimensioni proprie, in particolare un volume, e la loro massa è distribuita - secondo una propria densità - entro questo volume. Quest’approssimazione non lede i risultati previsti dalla fisica, qualora si voglia studiare il moto di un corpo nella sua interezza; ma se si è interessati al movimento specifico di una porzione del corpo, di come essa si muova rispetto alle altre, o a come un corpo esteso si muove in tutte le sue parti, il modello del punto materiale non è più sufficiente.
Il modello che si usa, allora, è quello del corpo continuo, ossia un volume occupato da una massa con densità propria. Un caso particolare di corpo continuo è costituito dal corpo rigido: si definisce corpo rigido un corpo continuo in cui i singoli punti geometrici che lo compongono rimangono ad una distanza fissata l’uno dall’altro. Di conseguenza, anche sotto l’azione di forze, un corpo rigido non subisce deformazioni.
Le forze però continuano a sortire gli effetti previsti dalle leggi di Newton: se più forze concorrono a causare un moto, occorrerà effetuarne la somma vettoriale, l’azione complessiva di tutte le forze sarà determinata da un’unica forza risultante. Ma qui sorge subito un problema: essendo il corpo rigido dotato di molti punti, che cosa succede se le forze sono applicate in punti differenti?

Grazie alla definizione di corpo rigido, possiamo risolvere anche questo caso. Infatti sussistono, in aggiunta alle regole della dinamica, le seguenti:
- il punto di applicazione di una forza può essere spostato lungo la retta individuata dalla direzione della stessa, detta retta di applicazione o retta d’azione, senza che sia modificato il suo effetto dinamico

Infatti, lo spostamento del punto di applicazione della forza non deforma in alcun modo il corpo, e non modifica nemmeno la direzione, il modulo e il verso della forza: essa viene trasmessa senza alterazioni, dalla rigidità del corpo stesso, lungo tutti i punti della propria retta d’azione. - l’effetto dinamico non viene modificato se, al sistema di forze esistente, si aggiunge una coppia di forze uguali in direzione (e dunque agenti sulla stessa retta d’azione) e modulo ma opposte in verso.

Infatti, per la proprietà precedente, possiamo immaginare di spostare i punti di applicazione delle coppie di forze fino a farli coincidere: ora, per come è definita la somma di due vettori, la forza risultante da queste due è pari al vettore nullo; il loro contributo dinamico è dunque altresì pari a $0$. - In generale, se due forze agiscono lungo direzioni che si intersecano (dunque, non parallele), possiamo ripetere il ragionamento e calcolare la forza risultante, come illustrato dalla figura, mediante la somma vettoriale:

Ma che cosa accade se le forze agiscono in direzione parallela? Dividiamo questa situazione in tre casi. I primi due produrranno una singola forza risultante; nel terzo caso, invece, non sarà possibile ridursi a una singola forza, e per spiegare l’effetto dinamico sarà necessario introdurre un nuovo ente fisico: il momento di una forza.
Caso 1: Forze agenti lungo direzioni parallele e di verso concorde.
Con riferimento alla figura seguente, chiamiamo $\vec{F}_1$ ed $\vec{F}_2$ le due forze, e $A$ e $B$, rispettivamente, i loro punti di applicazione.
In questo caso si può dimostrare che le forze sono equivalenti a un’unica forza $\vec{F}$ così determinata:
- Direzione parallela a quella di $\vec{F}_1$ ed $\vec{F}_2$, passante per il punto di applicazione $C$ (determinato in seguito)
- Verso pari a quello di $\vec{F}_1$ e $\vec{F}_2$
- Modulo pari alla somma dei moduli di ambo le forze: $ \left | \vec{F} \right | = \left | \vec{F}_1 \right | + \left | \vec{F}_2 \right |$
- Punto di applicazione $C$, sul segmento $\overline{AB}$, determinato di modo che il segmento $\overline{AB}$ sia diviso in segmenti di lunghezza inversamente proporzionale ai moduli delle forze date: cioè, deve valere la proporzione $\overline{AC} : \overline{CB} = \left | \vec{F}_2 \right | : \left | \vec{F}_1 \right | $.
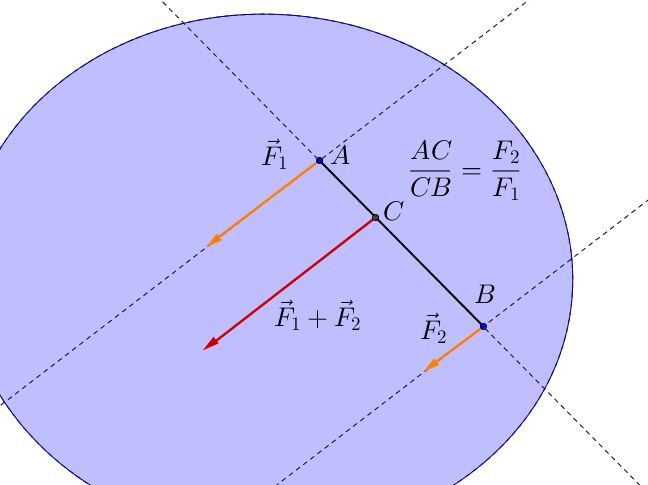
Facciamo notare che, se le forze sono in modulo uguale, il punto $C$ è il punto medio del segmento $AB$.
Caso 2: Forze agenti lungo direzioni parallele, di modulo differente e di verso discorde.
Questa volta il verso di $\vec{F}_1$ è opposto a $\vec{F}_2$. Facciamo notare che, avendo modulo differente, sicuramente una fra $\vec{F}_1$ ed $\vec{F}_2$ avrà modulo strettamente maggiore dell’altra. Ad ogni modo, l’effetto dinamico complessivo è comunque determinato da un’unica forza risultante, $\vec{F}$, così determinata:
- Direzione parallela a quella di $\vec{F}_1$ ed $\vec{F}_2$, passante per il punto di applicazione $C$ (determinato in seguito)
- Verso pari a quello della forza di modulo maggiore (in figura, $\vec{F}_1$)
- Modulo pari alla differenza dei due moduli: $\left | \vec{F} \right | = \left | \left |\vec{F}_1 \right | - \left | \vec{F}_2 \right | \right |$
- Punto di applicazione $C$, sul prolungamento del segmento $\overline{AB}$, dalla parte della forza di modulo maggiore, determinato di modo che il segmento i segmenti $\overline{AC}$ e $\overline{CB}$ siano di lunghezza inversamente proporzionale ai moduli delle forze date: cioè, deve ancora valere la proporzione $\overline{AC} : \overline{CB} = \left | \vec{F}_2 \right | : \left | \vec{F}_1 \right | $.

Caso 3: Forze agenti su direzioni parallele, di ugual modulo e di verso differente
In questo caso, le direzioni individuate dai vettori forza $\vec{F}_1$ ed $\vec{F}_2$ continuano ad essere parallele, il modulo dei due vettori è uguale ma il loro verso è discorde: questo caso particolare va sotto il nome di coppia di forze. Siccome sono uguali in modulo, di direzione parallela e discordi in verso, le forze $\vec{F}_1$ ed $\vec{F}_2$ possono essere scritte come $\vec{F}$ e $-\vec{F}$. Il motivo per cui viene trattato in maniera particolare è presto detto: la costruzione geometrica che si dovrebbe usare per costruire la risultante $\vec{F}$ di cui ai casi 1 e 2, è inconcludente; non riusciamo a ricondurci ad un’unica forza, o meglio, la forza risultante cui ci riconduciamo è nulla. L’effetto dinamico complessivo, però, è differente dagli altri casi. Nei casi 1 e 2, applicando la legge fondamentale della dinamica $\vec{F} = m \vec{a}$, ogni punto del corpo rigido viene accelerato di un’accelerazione pari a $\vec{a} = \frac{\vec{F}}{m}$, dove $m$ è la massa complessiva del corpo rigido: il caso si riduce ad un punto materiale “molto grosso”, il cui moto è completamente determinato dall’accelerazione appena descritta. Invece, nel caso della coppia di forze, il corpo rigido rimane complessivamente fermo, ma comincia a ruotare attorno a un asse.
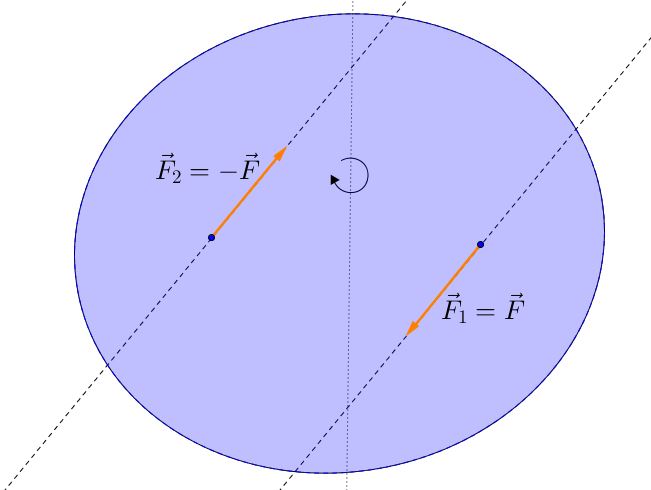
Il fatto che rimanga complessivamente fermo è in accordo con il fatto che la risultante trovata sia nulla, ma la rotazione come può essere spiegata? Per spiegare questo fenomeno dal punto di vista della meccanica è necessario introdurre il concetto di momento di una forza.
Momento di una forza rispetto a un asse
Supponiamo di avere un punto materiale $P$ libero di ruotare attorno ad un asse, identificato da una retta che chiameremo $a$; inoltre, sia applicata in $P$ una forza $\vec{F}$. Indichiamo con $\vec{r}$ il raggio-vettore che congiunge l’asse $a$ con il punto $P$: questo vettore prende il nome di braccio della forza $\vec{F}$. Chiamiamo infine $\alpha$ l’angolo compreso tra i vettori $\vec{F}$ ed $\vec{r}$. Si definisce allora momento della forza $\vec{F}$ rispetto all’asse $a$, detto anche momento meccanico, il vettore $\vec{M}$ così costruito:
- Direzione individuata dalla retta $a$
- Modulo pari al prodotto dei moduli del braccio $\vec{r}$ e della forza $\vec{F}$ e del seno dell’angolo $\alpha$: $ M = r \ F \ \sin(\alpha) $
- Verso dato da quello di una vite immaginaria che da $\vec{r}$ si avvita su $\vec{F}$, ovverosia dalla regola della mano destra.
Ricordando la definizione di prodotto vettoriale tra due vettori, possiamo definire il momento di una forza rispetto ad un asse in un’unica formula:$$\vec{M} = \vec{r} \times \vec{F}$$
Per la stessa definizione di momento rispetto ad un asse, notiamo che non importa da dove si conduce il braccio (eventuali componenti parallele ad $a$, infatti, verrebbero ad annullarsi effettuando il prodotto vettore), a patto che il punto di partenza di $\vec{r}$ sia sull’asse $a$ e il punto d’arrivo sia il punto $P$ di applicazione della forza.

Il momento di una forza rispetto ad un asse è una grandeza vettoriale che rende conto di quanto una determinata forza può imporre o meno una rotazione attorno ad un dato asse.
Si deve fare attenzione a non confondere il momento meccanico con la quantità di moto (anche detto momento lineare) e momento angolare, sebbene quest'ultime due quantità siano strettamente legate tra loro.
Momento di una coppia di forze
Torniamo al caso della coppia di forze. Anche in questo caso, è possibile ricondurre la rotazione impressa al corpo rigido dalla coppia di forze ad un momento, detto appunto momento della coppia di forze. Per definirlo, consideriamo una coppia di forze $\vec{F}$ ed $-\vec{F}$ applicate a due punti del corpo rigido $A$ e $B$. Detto $\vec{r}$ il vettore che unisce i punti $A$ e $B$, definiamo il momento della coppia di forze il vettore $\vec{M}$, ottenuto come prodotto vettore tra $\vec{r}$ ed $\vec{F}$: $$\vec{M} = \vec{r} \times \vec{F}$$

Questa definizione di momento di una coppia di forze è coerente con quella data di momento di una forza: come si vede nell’illustrazione seguente, comunque preso un asse $a$, la somma vettoriale dei momenti delle forze $\vec{F}$ e $-\vec{F}$ rispetto all’asse $a$ produce come risultato proprio il momento della coppia di forze.

Data questa proprietà, si può ben vedere come il momento di una singola forza sia legato all’asse prescelto, mentre una coppia di forze è caratterizzata, in modo intrinseco, da un proprio momento, indipendente da un asse di rotazione esterno: anzi, una coppia di forze stabilisce autonomamente un asse di rotazione.
Condizione di equilibrio per un corpo rigido
Il primo principio della dinamica asserisce la condizione di equilibrio per un punto materiale: occorre (e basta) che la somma vettoriale delle forze agenti sul punto sia nulla. Ma come abbiamo appena visto, anche in presenza di una forza complessiva nulla, l’effetto complessivo su un corpo rigido può comportare rotazioni: la condizione di equilibrio deve essere quindi “aggiornata” per il corpo rigido.
In presenza di più coppie di forze, definiamo il momento risultante come la somma vettoriale dei momenti di tutte le coppie di forze agenti sul corpo rigido: $\vec{M} = \sum_i \vec{M}_i$. Ogni momento di una coppia di forze sarà responsabile di una rotazione attorno ad un asse, e si può dimostrare che il contributo di tutti questi momenti è equivalente ad un’unica rotazione impressa da un unico momento di una coppia di forze, appunto il momento risultante.
La condizione di equilibrio per un corpo rigido allora diventa:
Un corpo rigido persiste nel suo stato di quiete o moto rettilineo uniforme se e solo se
- La Forza risultante, responsabile di moti traslatori, è nulla: $\displaystyle{\vec{F} = \sum_i \vec{F}_i = 0}$
- Il Momento risultante, responsabile di rotazioni, è nullo: $\displaystyle{\vec{M} = \sum_i \vec{M}_i = 0}$