Tra le curve che possiamo ottenere come sezione conica troviamo la parabola. Anche se queste curve possono essere “direzionate” in qualsiasi modo nel piano cartesiano, di solito quando le studiamo in Geometria Analitica consideriamo solamente le parabole con asse di simmetria parallelo a uno dei due assi cartesiani.

Definizione
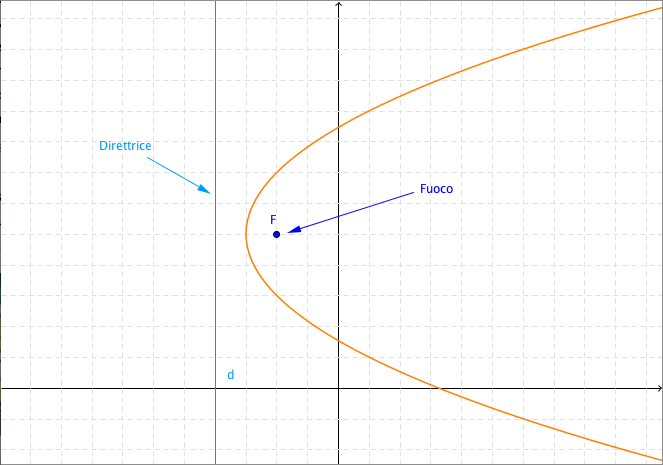
Prendiamo un punto $F$ e una retta $d$ nel piano, con $F \not \in d$. Il luogo dei punti del piano che hanno la stessa distanza da $F$ e da $d$ è detto parabola.
Il punto $F$ viene detto fuoco della parabola e la retta $d$ viene detta direttrice della parabola.
La definizione che abbiamo appena dato descrive una qualsiasi parabola nel piano, ma le parabole con asse di simmetria parallelo a uno degli assi cartesiani possono anche essere descritte con una equazione molto semplice:
- se l’asse di simmetria è parallelo all’asse $y$, la direttrice è parallela all'asse $x$ e l’equazione della parabola è del tipo: $$y = ax^2 + bx + c, \qquad a, b, c \in \mathbb{R}, a \neq 0;$$

- se l’asse di simmetria è parallelo all’asse $x$, la direttrice è parallela all'asse $x$ e l’equazione della parabola è del tipo: $$x = ay^2 + by + c, \qquad a, b, c \in \mathbb{R}, a \neq 0.$$
Le quantità $a, b, c$ descrivono algebricamente la parabola, e ne determinano anche le proprietà geometriche. A partire da esse, infatti, possiamo ricavare molte formule utili che ci permettono di studiare la parabola nel piano cartesiano. Suddivideremo la nostra analisi a seconda che l’asse di simmetria sia parallelo all’asse $x$ o all’asse $y$.
Parabola con asse di simmetria parallelo all’asse $y$
Ricordiamo che le parabole di questo tipo sono descritte da un’equazione del tipo: $$y = ax^2 + bx + c, \qquad a, b, c \in \mathbb{R}, a \neq 0.$$A partire da questa equazione possiamo studiare alcune quantità notevoli.
- Il parametro $a$, che è sempre diverso da zero, determina la concavità della parabola. In particolare, se $a > 0$ la parabola è rivolta verso l’alto, mentre se $a < 0$ la parabola è rivolta verso il basso.
Viene detto vertice della parabola il punto della parabola che ha ordinata minore o maggiore, a seconda che $a >0$ o $a<0$, rispettivamente. Conoscendo le coordinate $(x_V, y_V)$ del vertice $V$, l’equazione della parabola si può riscrivere anche come: $$y-y_V = a(x-x_V)^2, \quad a \neq 0$$
- La quantità $\Delta = b^2 - 4ac$, che è il delta del trinomio di secondo grado $ax^2 +bx + c$, viene semplicemente detto delta della parabola. A partire dal segno di $\Delta$ si possono scoprire quante sono le intersezioni della parabola con l’asse $x$:
- se $\Delta > 0$, le intersezioni sono due;
- se $\Delta = 0$, c’è una intersezione;
- se $\Delta < 0$, non ci sono intersezioni.
Elenchiamo le formule più utili per lo studio di una parabola di questo tipo.
Coordinate del vertice: $$V \equiv \left ( -\frac{b}{2a}, -\frac{\Delta}{4a} \right )$$
Coordinate del fuoco: $$F \equiv \left ( -\frac{b}{2a}, \frac{1-\Delta}{4a} \right )$$
Equazione della direttrice: $$d : \quad y = -\frac{1+\Delta}{4a}$$
Equazione dell’asse di simmetria: $$a: \quad x = -\frac{b}{2a}$$
Da quanto appena ottenuto possiamo ricavare facilmente che la distanza $\overline{FV}$ tra fuoco e vertice e che la distanza $\text{dist}(d, V)$ tra direttrice e vertice sono uguali e pari a$$ \overline{FV} = \text{dist}(d, V) = \frac{1}{4a}.$$
Tangenti a una parabola con asse di simmetria parallelo all’asse $y$
Prendiamo una parabola di equazione $y = ax^2 + bx +c, a \neq 0$. Supponiamo di voler determinare le rette passanti per un punto $P \equiv (x_0, y_0)$ del piano che siano anche tangenti alla parabola data.
La procedura standard per risolvere questo problema prevede per prima cosa di mettere a sistema il fascio di rette passanti per $P$ con la parabola: $$\begin{cases} y = ax^2 + bx + c \\ y-y_0 = m(x-x_0) \end{cases}$$Successivamente, bisogna richiedere che questo sistema abbia una sola soluzione (che corrisponderà all’unico punto di intersezione tra la parabola e la retta): questa richiesta equivale ad imporre che l’equazione risolvente del sistema di secondo grado (che risulterà essere un’equazione di secondo grado) abbia delta uguale a zero.
Saltando i passaggi algebrici, possiamo affermare che questo problema si può ricondurre a trovare le soluzioni di questa equazione di secondo grado in $m$: $$\mathbf{m}^2 - 2(b+2ax_0)\mathbf{m} + \Delta + 4ay_0 = 0$$In sostanza, le (eventuali) soluzioni $m_1, m_2$ di questa equazione saranno proprio i coefficienti angolari delle rette tangenti alla parabola passanti per $P$.
Questa equazione di secondo grado in $m$ avrà un delta $\delta$ (da non confondere con $\Delta$, che è relativo alla parabola!): svolgendo i conti, otteniamo: $$\delta = 4a(ax_0^2 + bx_0 + c - y_0)$$Il segno di $\delta$ ci permetterà di capire se e quando esistono le soluzioni $m_1, m_2$.
- Dato che $a \neq 0$, allora $\delta = 0 \Leftrightarrow y_0 = ax_0^2 + bx_0 + c$, condizione che è verificata quando $P$ appartiene alla parabola. Quindi quando $P$ è sulla parabola c’è un’unica tangente alla parabola con coefficiente angolare $m$, in accordo con l’intuizione geometrica. Il valore di questo coefficiente $m$ è dato dalla formula: $$m = b + 2ax_0$$o alternativamente dalla formula: $$m = 2a(x_0 - x_V)$$dove $x_V = -\frac{b}{2a}$ è la ascissa del vertice $V$ della parabola.

Se inseriamo il valore di $m$ all’interno della formula $y-y_0 = m(x-x_0)$, otteniamo l’equazione della retta tangente $r$ a una parabola in un suo punto $P \equiv (x_0, y_0)$, che può anche essere riscritta con la formula di sdoppiamento: $$r: \quad \frac{y+y_0}{2} = axx_0 + b\frac{x+x_0}{2} + c$$ - Con ragionamenti algebrici su $\delta$, si può mostrare che $\delta > 0$ quando $P$ è all’esterno della parabola, sempre in accordo con l’intuizione geometrica. In questo caso abbiamo dunque due rette tangenti alla parabola con coefficienti angolari $m_1, m_2$ dati dalle formule:
##KATEX##\begin{aligned}m_1 & = b + 2ax_0 + 2\sqrt{a(ax_0^2 + bx_0 + c - y_0)} \\m_2 & = b + 2ax_0 - 2\sqrt{a(ax_0^2 + bx_0 + c - y_0)}\end{aligned}##KATEX##
o anche:
##KATEX##\begin{aligned}m_1 & = 2a(x_0 - x_V) + 2\sqrt{a(a(x_0 - x_V)^2 - (y_0 - y_V))} \\m_2 & = 2a(x_0 - x_V) - 2\sqrt{a(a(x_0 - x_V)^2 - (y_0 - y_V))}\end{aligned}##KATEX##
dove il vertice $V$ ha coordinate $(x_V, y_V)$.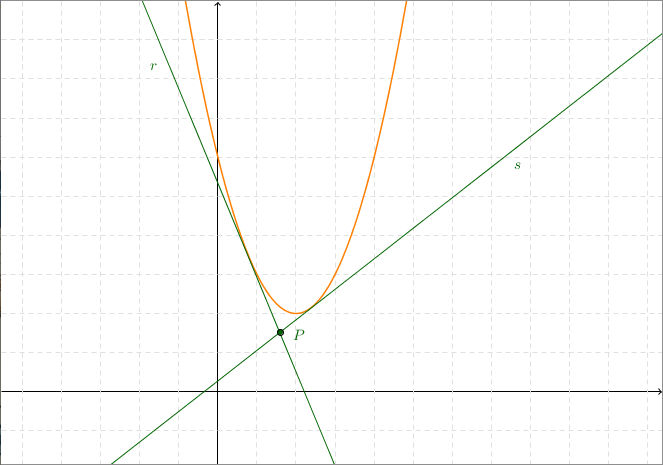
- Se il punto $P$ è invece interno alla parabola, non ci sono rette tangenti alla parabola data passanti per $P$.
Parabola con asse di simmetria parallelo all’asse $x$
Le parabole di questo tipo sono descritte da un’equazione del tipo: $$x = ay^2 + by + c, \qquad a, b, c \in \mathbb{R}, a \neq 0.$$
- Il parametro $a$, che è sempre diverso da zero, determina se la parabola è “rivolta verso destra” (se $a > 0$) o se è “rivolta verso sinistra” (se $a < 0$).
Viene detto vertice della parabola il punto della parabola che ha ascissa minore o maggiore, a seconda che $a >0$ o $a<0$, rispettivamente. Conoscendo le coordinate $(x_V, y_V)$ del vertice $V$, l’equazione della parabola si può riscrivere anche come: $$x-x_V = a(y-y_V)^2, \quad a \neq 0$$ - La quantità $\Delta = b^2 - 4ac$, che è il delta del trinomio di secondo grado $ay^2 +by + c$, viene nuovamente detta delta della parabola. A partire dal segno di $\Delta$ si possono scoprire quante sono le intersezioni della parabola con l’asse $y$:
- se $\Delta > 0$, le intersezioni sono due;
- se $\Delta = 0$, c’è una intersezione;
- se $\Delta < 0$, non ci sono intersezioni.
Ecco le formule per lo studio di una parabola di questo tipo.
Coordinate del vertice: $$V \equiv \left ( -\frac{\Delta}{4a}, -\frac{b}{2a}\right )$$
Coordinate del fuoco: $$F \equiv \left ( \frac{1-\Delta}{4a}, -\frac{b}{2a} \right )$$
Equazione della direttrice: $$d : \quad x = -\frac{1+\Delta}{4a}$$
Equazione dell’asse di simmetria: $$a: \quad y = -\frac{b}{2a}$$
Anche in questo caso la distanza $\overline{FV}$ tra fuoco e vertice e la distanza $\text{dist}(d, V)$ tra direttrice e vertice sono uguali e pari a$$ \overline{FV} = \text{dist}(d, V) = \frac{1}{4a}$$
Tangenti a una parabola con asse di simmetria parallelo all’asse $x$
Data una parabola di equazione $x = ay^2 + by +c, a \neq 0$, supponiamo di voler determinare le rette tangenti ad essa e passanti per un punto $P \equiv (x_0, y_0)$ del piano.
Analogamente a quanto abbiamo fatto per le tangenti ad una parabola con asse parallelo all’asse $x$, bisogna mettere a sistema il fascio di rette passanti per $P$ con la parabola e imporre che l’equazione risolvente abbia delta uguale a zero. Dopo alcuni (laboriosi) conti, si vede che questo problema si può ricondurre a trovare le soluzioni di questa equazione in $m$: $$(\Delta+4ax_0)\mathbf{m}^2 - 2(b+2ay_0)\mathbf{m} + 1 = 0$$Dobbiamo distinguere due casi.
- Se $\Delta+4ax_0 = 0$, cioè quando $x_0 = -\frac{\Delta}{4a} = x_V$, questa equazione è di primo grado in $m$. Se supponiamo che $P$ non sia il vertice, svolgendo i conti otteniamo una sola soluzione: $$m = \frac{1}{2 ( b+2ay_0)} = \frac{1}{4a(y_0 - y_V)}$$Questo tuttavia non deve farci credere che ci sia una sola tangente alla parabola passante per $P$: infatti c’è anche la retta $r: x = x_V = -\frac{\Delta}{4a}$, che passa proprio per $P$ ed è tangente alla parabola nel vertice $V$.

Se invece $P \equiv V$, allora la tangente è effettivamente solo una ed è proprio la retta $r: x = x_0$. - Quando $x_0 \neq x_V$, l’equazione è di secondo grado in $m$. Le (eventuali) soluzioni $m_1, m_2$ di questa equazione saranno i coefficienti angolari delle rette tangenti alla parabola passanti per $P$.
Il delta $\delta$ dell’equazione è dato dall’espressione:$$\delta = 4a(ay_0^2 + by_0 + c - x_0).$$Il segno di $\delta$ ci permetterà di capire se e quando esistono le soluzioni $m_1, m_2$.- Si ha che $\delta = 0 \Leftrightarrow y_0 = ax_0^2 + bx_0 + c$, condizione che è verificata quando $P$ appartiene alla parabola. Quindi quando $P$ è sulla parabola c’è un'unica tangente alla parabola con coefficiente angolare $m$.
Il valore di questo coefficiente $m$ è dato dalla formula: $$m = \frac{b + 2ay_0}{\Delta + 4ax_0}$$o alternativamente dalla formula: $$m = \frac{(y_0 - y_V)}{2(x_0-x_V)}$$ - Si può mostrare che $\delta > 0$ quando $P$ è all’esterno della parabola. In questo caso abbiamo dunque due rette tangenti alla parabola con coefficienti angolari $m_1, m_2$ dati dalle formule:
##KATEX##\begin{aligned}m_1 & = \frac{1}{\Delta + 4ax_0} \cdot \left ( b + 2ay_0 + 2\sqrt{a(ay_0^2 + by_0 + c - x_0)} \right ) \\m_2 & = \frac{1}{\Delta + 4ax_0} \cdot \left ( b + 2ay_0 - 2\sqrt{a(ay_0^2 + by_0 + c - x_0)} \right )\end{aligned}##KATEX##
o anche:
##KATEX##\begin{aligned}m_1 & = \frac{1}{4a(x_0-x_V)} \cdot \left ( 2a(y_0 - y_V) + 2\sqrt{a(a(y_0 - y_V)^2 - (x_0 - x_V))} \right ) \\m_2 & = \frac{1}{4a(x_0-x_V)}\cdot \left ( 2a(y_0 - y_V) - 2\sqrt{a(a(y_0 - y_V)^2 - (x_0 - x_V))} \right )\end{aligned}##KATEX## - Se il punto $P$ è invece interno alla parabola, non ci sono rette tangenti alla parabola data passanti per $P$.
- Si ha che $\delta = 0 \Leftrightarrow y_0 = ax_0^2 + bx_0 + c$, condizione che è verificata quando $P$ appartiene alla parabola. Quindi quando $P$ è sulla parabola c’è un'unica tangente alla parabola con coefficiente angolare $m$.