Un quadrato magico è una tabella di forma quadrata (una matrice quadrata, sostanzialmente) contenente tutti numeri distinti, tale per cui la somma degli elementi presenti su ciascuna riga, ciascuna colonna e ciascuna diagonale sia sempre pari allo stesso numero.
Il numero di caselle di cui è composto un quadrato magico (o, utilizzando il linguaggio delle matrici, l’ordine della matrice quadrata che lo rappresenta) è detto ordine del quadrato magico.
Al giorno d’oggi, questi oggetti matematici fanno parte della cosiddetta matematica ricreativa, e non hanno grande rilevanza all’interno della ricerca matematica moderna. In passato, tuttavia, i quadrati magici sono stati studiati in maniera approfondita da molti matematici e studiosi. A essi, inoltre, erano attribuiti significati mistici e proprietà magiche (da cui il loro nome): per esempio, Cornelio Agrippa (1486 - 1535) scrisse nel suo De Occulta Philosophia riguardo a sette quadrati magici di ordine variabile da 3 a 9, assegnando a ciascuno di essi uno dei sette pianeti classici (Saturno, Giove, Marte, Sole, Venere, Mercurio e Luna). In ogni caso, le prime testimonianze dei quadrati magici risalgono addirittura al VI secolo a.C., all’interno della cultura e della tradizione cinese; sappiamo inoltre che i quadrati magici erano conosciuti anche da matematici arabi, persiani e indiani.
I quadrati magici, così come è accaduto con altri oggetti matematici (come per esempio la sezione aurea), hanno affascinato e sedotto molti artisti, a causa delle misteriose proprietà esoteriche a essi attribuite. Tra gli esempi più celebri ricordiamo la presenza di un quadrato magico di ordine $4$ in nell’incisione Melencholia I di Albrecht Dürer (1471 – 1528), risalente al 1514, ancora oggi oggetto di interpretazioni.

Anche Antoni Gaudì (1852 – 1926) inserì un quadrato magico di ordine $4$, raffigurandolo su una facciata della sua Sagrada Família, a Barcellona: in realtà, quest’ultimo è solo un “parente” di un quadrato magico, dato che alcuni numeri si ripetono più di una volta. È interessante notare che la somma delle sue righe, colonne e diagonali (e in realtà anche di altre “forme” interne al quadrato) fa sempre $33$, pari agli anni di Cristo al tempo della Passione.

Proprietà e costruzione di un quadrato magico
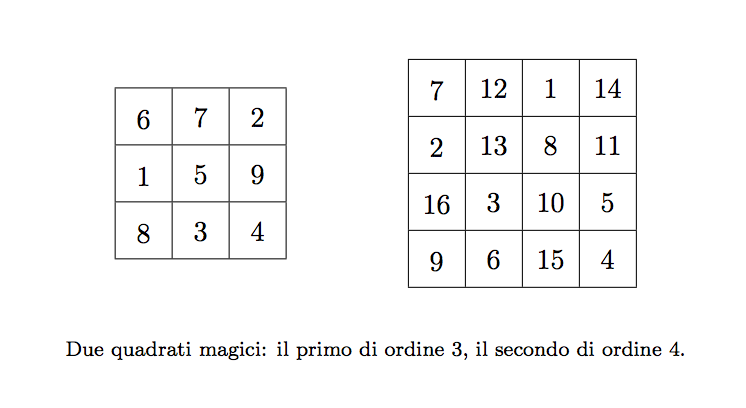
Un quadrato magico, per costruzione, conterrà sempre $n^2$ numeri distinti, dove $n$ è l’ordine del quadrato considerato. Se il quadrato magico contiene i primi $n^2$ numeri naturali, allora il quadrato magico è detto normale. Il quadrato magico di ordine $3$ mostrato all'inizio della lezione è in effetti un quadrato magico normale, e infatti contiene tutti i numeri da $1$ a $3^2 = 9$.
La proprietà più importante che riguarda un quadrato magico normale di ordine $n$ è che la somma dei numeri su tutte le righe, colonne e diagonali è univocamente determinata dall’ordine del quadrato stesso, come afferma il seguente teorema.
TEOREMA: La somma dei numeri presenti su una qualsiasi riga, colonna o diagonale di un quadrato magico normale di ordine $n$ è sempre pari alla costante magica $M_n$ del quadrato, che dipende solamente da $n$ e non dal modo in cui sono disposti i numeri al suo interno. Tale costante, inoltre, si può trovare con questa formula: $$M_n = \frac{n (n^2 + 1) }{2}. $$Dimostrazione. Supponiamo di avere un quadrato magico normale di ordine $n$ qualsiasi. Consideriamo la somma di tutti i numeri contenuti al suo interno, che chiamiamo $A$: $$A = 1+2+3+\ldots + (n^2-1) + n^2$$Esiste una formula generale per determinare $A$ a partire dal valore di $n$, di cui omettiamo la dimostrazione: $$A = \frac{n^2(n^2+1)}{2}.$$Consideriamo adesso le righe del quadrato magico considerato. Per ipotesi, la somma dei numeri contenuti in ciascuna di queste righe è pari a $M_n$: quindi la somma totale di tutte le somme delle righe del quadrato è uguale a $n \cdot M_n$, dato che, in totale, le righe del quadrato sono $n$.
A questo punto, però, è sufficiente riflettere un momento per rendersi conto di questo: la “somma delle somme” delle righe del quadrato è uguale alla somma di tutti gli elementi del quadrato! Vale cioè la seguente relazione: $$A = n \cdot M_n$$A questo punto è facile ricavare che $$M_n = \frac{A}{n} = \frac{1}{n} \frac{n^2 (n^2 + 1) }{2} = \frac{n (n^2 + 1) }{2}.$$Questo è esattamente quello che volevamo dimostrare. Notiamo inoltre che non sono state fatte ipotesi sulla disposizione dei numeri all’interno del quadrato: quindi questa formula è valida per qualsiasi quadrato normale di ordine $n$.
Ecco alcune altre proprietà relative a un quadrato magico.
- Se aggiungiamo o sottraiamo la stessa quantità $a$ a ciascun numero di un quadrato magico, otteniamo di nuovo un quadrato magico. Un quadrato magico normale a cui abbiamo aggiunto o sottratto $a$ ha costante magica $M_n + na$ o $M_n - na$, rispettivamente.
- Se moltiplichiamo ciascun numero di un quadrato magico per la stessa costante $k$ otteniamo di nuovo un quadrato magico. Un quadrato magico normale moltiplicato per $k$ ha come costante magica $kM_n$.
- Prendiamo un quadrato magico normale di ordine $n$, e consideriamo il quadrato ottenuto sottraendo a $n^2+1$ ogni numero del quadrato di partenza. Questo nuovo quadrato è magico e normale (e quindi ha la stessa costante magica).
- Ciascun quadrato magico rimane magico se ruotato di $90$, $180$ o $270$ gradi, oppure se viene riflesso rispetto all’asse orizzontale, verticale e a ciascuna delle sue diagonali.
Metodo di costruzione di quadrati magici normali di ordine dispari
C’è un metodo abbastanza semplice per costruire un quadrato magico normale di ordine dispari (anche se non è certamente l’unico).
La regola per la costruzione consiste dei seguenti passi. Posizioniamo un $1$ nell’elemento centrale della prima riga, e successivamente, spostandoci di una posizione a destra e di una posizione in alto nel quadrato, posizioniamo i numeri successivi della sequenza ($2$, $3$, $4$ e così via fino ad arrivare a $n^2$) con i seguenti accorgimenti:
- se non è possibile spostarsi in alto o a destra nel quadrato, ci si sposta nella riga più in basso o nella riga più a sinistra, rispettivamente;
- se si incontra una posizione già occupata da un numero, bisogna posizionare il numero nello spazio libero immediatamente sotto all’ultimo numero scritto.
Ecco per esempio la costruzione di un quadrato magico normale di ordine $5$:

Altre curiosità sui quadrati magici
Successivamente all’avanzamento degli strumenti matematici a nostra disposizione, sono state trovate numerose proprietà e particolarità legate ai quadrati magici. Elenchiamo qui di seguito quelle più interessanti.
- A meno di considerare “uguali” i quadrati magici normali che sono ottenibili l’uno dall’altro tramite rotazioni e riflessioni (applicando cioè una relazione di equivalenza nell’insieme dei quadrati magici normali), sappiamo che esistono solo:
- un quadrato di ordine $1$ (costituito solamente dal numero $1$!);
- nessun quadrato di ordine $2$;
- solamente un quadrato di ordine $3$;
- $880$ quadrati di ordine $4$, determinati nel XVII secolo da Bernard Frénicle de Bessy;
- $275305224$ quadrati di ordine $5$, elencati utilizzando moderni metodi di calcolo nel 1973.
- L’elenco visto al punto precedente non è attualmente ampliabile: infatti, determinare quanti sono i quadrati magici di ordine $n > 6$ è ancora oggi un problema aperto, poichè non esiste un metodo che riesca a fornire esaustivamente tutti i quadrati magici di un dato ordine $n$. Si stima, comunque, che il numero di quadrati magici di ordine $6$ si aggiri intorno a $10^{19}$.
- Per rimanere nell’ambito della cabala e della numerologia, è interessante notare che la somma dei numeri interni un quadrato magico normale di ordine $6$ è pari a $666$, numero “diabolico” per eccellenza.
- Esistono quadrati magici che, elevando tutti i numeri contenuti al loro interno a un esponente minore o uguale di un certo numero naturale $k$ assegnato, rimangono magici. Se $k=2$ questi si chiamano quadrati bimagici, se $k=3$ sono detti quadrati trimagici, e così via. In generale questi quadrati magici sono detti quadrati multimagici.
Nel 2001 è stato esibito il primo esempio di quadrato pentamagico; esso ha ordine $1024$. Non si conoscono esempi di quadrati esamagici, o in generale di quadrati multimagici relativi a $k>5$. - È possibile costruire anche cubi magici, ovvero “tabelle tridimensionali” di numeri tali per cui la somma di ogni possibile riga, colonna e diagonale del cubo sia pari allo stesso numero. L’ordine di un cubo è il numero di caselle che costituiscono un qualsiasi suo spigolo.
Analogamente a quanto accade per i quadrati, esistono anche cubi magici normali contenenti i numeri da $1$ a $n^3$, che ammettono costante magica data dalla formula $$M_n = \frac{n(n^3+1)}{2}.$$È possibile anche definire cubi multimagici; per esempio, attualmente siamo a conoscenza di due cubi tetramagici di ordine $1024$ e $8192$.