La sezione aurea, o rapporto aureo, è il nome che viene dato ad una particolare costante matematica che, solitamente, si indica con la lettera greca $\phi$. Questo numero è irrazionale, e quindi possiamo fornire solo una approssimazione del suo sviluppo decimale: $$\phi = 1,6180339887 \ldots$$Per secoli, questo numero ha affascinato e influenzato generazioni di matematici, ma anche pittori, architetti, scultori e persino musicisti. Alcuni esempi celebri sono:
- il Partenone, le cui dimensioni seguono le proporzioni del rettangolo aureo (che illustreremo più avanti);
- molti dipinti di Leonardo da Vinci, tra cui la Gioconda e l’Ultima Cena, sono stati realizzati seguendo complesse strutture geometriche che fanno uso della costante $\phi$;
- il compositore francese Claude Debussy scrisse alcuni brani seguendo particolari relazioni numeriche che rimandano proprio a questo numero.
Come ottenere la sezione aurea $\phi$
Consideriamo un segmento qualsiasi $AB$. Vogliamo prolungare $AB$ in modo da ottenere un nuovo segmento $AC$ che rispetti la proporzione: $$AC : AB = AB : BC$$Come facciamo a trovare il punto $C$? A che distanza da $A$ dobbiamo posizionarlo?
Per rispondere a questa domanda conviene affrontare il problema dal punto di vista algebrico. Poniamo $AC = x$ e chiamiamo $a$ la lunghezza di $AB$. La relazione che definisce $AC$ può essere riscritta così: $$x : a = a : (x-a)$$dove abbiamo utilizzato il fatto che $BC = AC - AB = x-a$.

Utilizzando il linguaggio delle proporzioni, che afferma che il prodotto dei medi è uguale al prodotto degli estremi, otteniamo la relazione $x \cdot (x-a) = a \cdot a$, che può essere riscritta così:$$x^2 - ax - a^2 = 0$$Questa è una equazione di secondo grado nell’incognita $x$, le cui soluzioni sono: $$x_1 = \frac{a + \sqrt{a^2 + 4a^2}}{2} = a \cdot \frac{1+\sqrt{5}}{2}, \qquad x_2 = \frac{a - \sqrt{a^2 + 4a^2}}{2} = a \cdot \frac{1-\sqrt{5}}{2}$$Dato che $\sqrt{5} > 1$ risulta $x_2 < 0$ e $x_1 > 0$; di conseguenza, dato che $x$ rappresenta la lunghezza di un segmento, solo $x = x_1 = a \frac{1+\sqrt{5}}{2}$ è accettabile.
A questo punto definiamo il rapporto aureo come il rapporto $\phi = \frac{x}{a}$, cioè: $$\phi = \frac{a \frac{1+\sqrt{5}}{2}}{a} = \frac{1+\sqrt{5}}{2}$$Come si può verificare facilmente con una calcolatrice, il valore che abbiamo appena assegnato a $\phi$ coincide con quello che abbiamo dato all’inizio della lezione per la sezione aurea, e cioè $\phi = 1,618033 \ldots$
Notiamo infine che se prendiamo l’equazione $x^2 - ax - a^2 = 0$ da cui siamo partiti e dividiamo entrambi i membri per $a^2$, otteniamo: $$\frac{x^2 - ax - a^2}{a^2} = 0 \quad \Rightarrow \quad \left ( \frac{x}{a} \right )^2 - \frac{x}{a} - 1 = 0 \quad \Rightarrow \quad \phi^2 - \phi - 1 = 0$$È importante memorizzare l’ultima equazione, dato che da essa discendono numerose curiosità legate a $\phi$.
Che cos’ha di speciale $\phi$?
La sezione aurea ha un numero impressionante di proprietà, ciascuna delle quali caratterizza notevolmente questo numero. Elenchiamo qui di seguito quelle di principale interesse.
- Il quadrato di $\phi$ è uguale a $\phi$ aumentato di $1$. Questa proprietà discende direttamente dall’equazione $\phi^2 - \phi - 1 = 0$, dato che può essere formulata come $\phi^2 = \phi + 1$; in ogni caso possiamo verificarla direttamente, dato che: $$\phi^2 = \left ( \frac{1 + \sqrt{5}}{2} \right )^2 = \frac{1+5+2\sqrt{5}}{4} = \frac{4 + 2+2\sqrt{5}}{4} = 1 + \frac{1+\sqrt{5}}{2} = 1 + \phi$$
- Il reciproco di $\phi$ è uguale a $\phi$ diminuito di $1$. Questa proprietà discende nuovamente dall’equazione $\phi^2 - \phi - 1 = 0$, dato che dividendo entrambi i membri per $\phi$ otteniamo: $$\frac{\phi^2}{\phi} = \frac{\phi + 1}{\phi} \quad \Rightarrow \quad \phi = 1 + \frac{1}{\phi} \quad \Rightarrow \quad \frac{1}{\phi} = \phi - 1$$In ogni caso possiamo verificare direttamente questa proprietà dato che:
##KATEX##\begin{aligned}\frac{1}{\phi} & = \frac{2}{1 + \sqrt{5}} = \frac{2}{1 + \sqrt{5}} \cdot \frac{ 1-\sqrt{5}}{1-\sqrt{5}} = \\& = \frac{2 - 2\sqrt{5}}{-4} = -\frac{4-2 - 2\sqrt{5}}{4} = \\& = -1 - \frac{-1-\sqrt{5}}{2} = \\& = -1 + \phi\end{aligned}##KATEX## - Le proprietà che abbiamo appena esposto indicano, tra le altre cose, che il quadrato e il reciproco di $\phi$ hanno la stessa parte decimale di $\phi$:
##KATEX##\begin{aligned}\phi & = 1,6180339887 \ldots \\\phi^2 & = 2,6180339887 \ldots \\\frac{1}{\phi} & = 0,6180339887 \ldots\end{aligned}##KATEX##
Inoltre, $\phi$ è l’unico numero per cui si verifica questa situazione (se escludiamo i numeri naturali, ovviamente). - La sezione aurea rispetta la seguente uguaglianza: $$\phi^{n+1} = \phi^n + \phi^{n-1}, \quad \forall \ n \in \mathbb{N}.$$
- Prendiamo la successione di Fibonacci $f_n$, di cui ricordiamo la definizione per ricorsione: $$\begin{cases} f_1 = 1 \\ f_2 = 1 \\ f_n = f_{n-1} + f_{n-2} \quad \forall \ n \in \mathbb{N}, n >2 \end{cases}$$I primi termini della successione sono dunque $1, 1, 2, 3, 5, 8, 13, 21, 34, 55 \ldots$. Si può mostrare che il rapporto $\frac{f_n}{f_{n+1}}$ tra due numeri consecutivi della successione diventa sempre più simile a $\phi$, al crescere di $n$: in altri termini: $$\frac{f_n}{f_{n+1}} \xrightarrow[n \to +\infty] {} \phi$$Esiste anche una formula per ricavare il termine generico $f_n$ della successione di Fibonacci, basato proprio sul rapporto aureo: $$f_n = \frac{\phi^n - \left ( 1-\phi \right )^n}{\sqrt{5}}$$
- Il rapporto tra la diagonale e il lato di un pentagono regolare è uguale al rapporto aureo $\phi$.
- Vale la relazione $\phi = 2 \cos \left ( \frac{\pi}{5} \right )$.
Il rettangolo aureo
Utilizzando $\phi$, possiamo costruire alcune interessanti figure geometriche. Il primo esempio di figura aurea è il rettangolo aureo, che è un rettangolo le cui dimensioni $a$ e $b$ sono in rapporto aureo: cioè $\frac{a}{b} = \phi$.

Ecco alcune proprietà legate al rettangolo aureo:
- quando al suo interno tracciamo un quadrato di lato uguale al lato minore del rettangolo come mostrato in figura, otteniamo un altro rettangolo aureo;

- se colleghiamo i 12 vertici di un icosaedro regolare a gruppi di 4 come mostrato in figura, otteniamo tre rettangoli aurei.

Possiamo ricavare le formule relative a un rettangolo aureo, a partire dalla misura del suo lato minore $b$ o dal lato maggiore $a$:
Area: $A = \phi \cdot b^2$, oppure $A = \frac{a^2}{\phi} = a^2 (\phi - 1)$
Perimetro: $2p = 2b (1 + \phi ) = 2b\phi^2$, oppure $2p = 2a ( \frac{1}{\phi} + 1 ) = 2a \phi$
Diagonale: $d = b\sqrt{2+\phi}$, oppure $d = \frac{a}{\phi}\sqrt{2+\phi}$
Triangolo di Keplero
Un triangolo rettangolo i cui l’ipotenusa $c$ e un cateto $a$ siano in rapporto aureo, cioè tali che $\frac{c}{a} = \phi$ è detto triangolo di Keplero.

L’enunciato del teorema di Pitagora, applicato a questo triangolo, è equivalente alla formula che abbiamo utilizzato per trovare algebricamente $\phi$. Infatti si ha $b^2 = c^2 - a^2 = (a \phi)^2 - a^2 = a^2(\phi^2 - 1) = a^2 \phi$, e quindi riformulando il tutto otteniamo: $$a^2 \phi + a^2 = a^2\phi^2 \quad \Rightarrow \quad \phi + 1 = \phi^2$$
Triangolo aureo
Un triangolo isoscele in cui uno dei due lati congruenti $b$ è in rapporto aureo con la base $a$ del triangolo è detto triangolo aureo.

Si può mostrare che l’angolo al vertice $\theta$ è acuto, e che $\theta = \frac{\pi}{5}$ radianti, cioè $36$ gradi. Dato che gli angoli alla base sono congruenti, essi misurano $\frac{180 - 36}{2} = 72$ gradi, cioè il doppio dell’angolo al vertice. Questa proprietà caratterizza completamente questo triangolo: ovvero, è possibile definire come “triangolo aureo” un triangolo che abbia due angoli congruenti e uguali al doppio dell’angolo rimanente.
Possiamo inoltre dividere facilmente un triangolo aureo in due triangoli, in modo che uno dei due sia un triangolo aureo e l’altro uno gnomone aureo (che definiremo tra poco). Basta infatti tracciare la bisettrice di uno degli angoli alla base e considerare i due triangoli che si vengono a formare all’interno del triangolo dato.
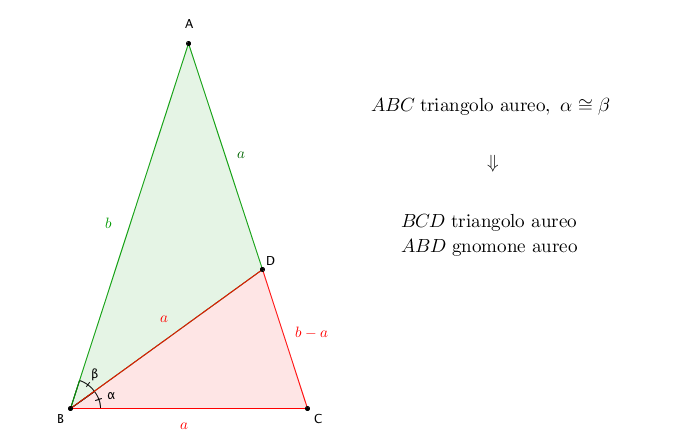
Inoltre, se consideriamo due diagonali di un pentagono regolare che hanno un estremo in comune, si può mostrare che esse formano un triangolo aureo con uno dei lati del pentagono:
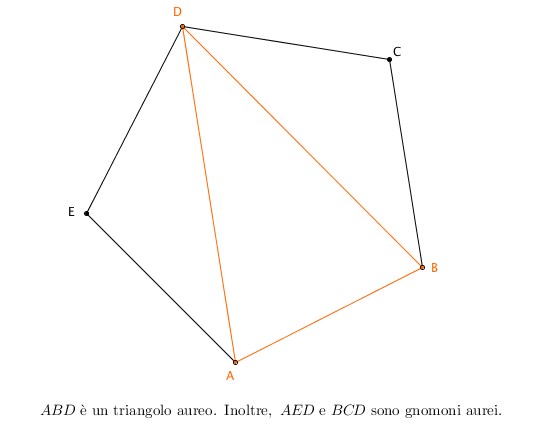
Gnomone aureo
Si chiama gnomone aureo un triangolo isoscele in cui il rapporto tra la base $a$ e uno qualsiasi dei due lati congruenti $b$ è uguale a $\phi$.

L’angolo al vertice $\theta$ misura $\frac{3\pi}{5}$ radianti, cioè $108$ gradi, e quindi gli angoli alla base misurano $36$ gradi ciascuno, cioè un terzo dell’angolo al vertice. In effetti è possibile definire uno gnomone aureo in base a questa proprietà degli angoli: ovvero, uno gnomone aureo è un triangolo che abbia due angoli congruenti, uguali a un terzo dell’angolo al vertice.
Possiamo suddividere uno gnomone aureo in due triangoli, uno dei quali è un triangolo aureo e l’altro è di nuovo uno gnomone aureo. Basta infatti considerare la semiretta che divide l’angolo al vertice in due parti $\alpha = 72^\circ$ e $\beta = 36^\circ$, e considerare i triangoli che si vengono a formare all’interno del triangolo dato.

Crediti immagine: Three golden rectangles in an icosahedron by Fropuff, Mysid - http://en.wikipedia.org/wiki/Golden_rectangle#/media/File:Icosahedron-golden-rectangles.svg