Uno dei teoremi più famosi di tutta la Geometria Euclidea è il teorema di Pitagora. Esso afferma che il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti del triangolo considerato. La sua dimostrazione viene attribuita, come dice il nome, al matematico greco Pitagora, anche se è probabile che altre civiltà abbiano scoperto questo teorema ben prima della sua nascita (o comunque, indipendentemente da Pitagora).
TEOREMA (di Pitagora): Dato un triangolo rettangolo $ABC$ come in figura, allora vale la relazione $$a^2 + b^2 = c^2$$ dove $c$ è l’ipotenusa del triangolo e $b, a$ sono i cateti.
Da questo teorema si possono ricavare le seguenti formule, che permettono di ricavare la misura di un lato a partire dagli altri due:
##KATEX##\begin{aligned}c & = \sqrt{b^2+a^2}; \\b & = \sqrt{c^2-a^2}; \\a & = \sqrt{c^2-b^2}.\end{aligned}##KATEX##
Per capire come utilizzare queste formule, facciamo un esempio: consideriamo un triangolo rettangolo con $c=10$ cm e $b=6$ cm. Allora $$a = \sqrt{c^2 - b^2} = \sqrt{100-36} = \sqrt{64} = 8 \text{ cm}.$$
Esistono molte dimostrazioni del Teorema di Pitagora (anzi, moltissime!) ma, per brevità, tra queste ne proponiamo solo due, entrambe esposte in maniera non rigorosa ma di grande impatto e di facile comprensione.
- Il primo teorema di Euclide afferma che il quadrato costruito su un cateto è equivalente al rettangolo avente come dimensioni la proiezione del cateto sull’ipotenusa e l’ipotenusa stessa. La figura che segue mostra come si può usare questo risultato per dimostrare il Teorema di Pitagora (aree uguali hanno gli stessi colori);
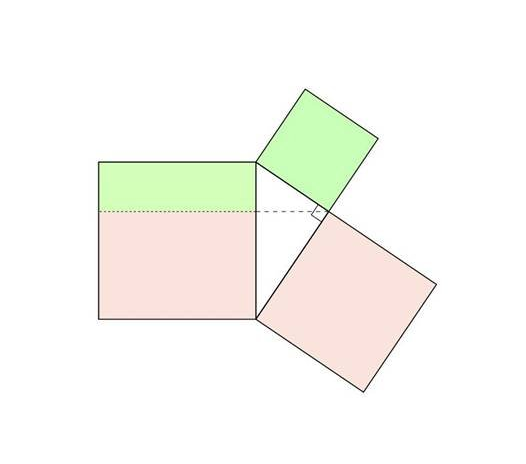
- La prossima immagine mostra come si possa ottenere una dimostrazione del Teorema con un semplice movimento rigido delle figure che la compongono:

Crediti immagine: JohnBlackburne - http://commons.wikimedia.org/wiki/File:Pythag_anim.gif#mediaviewer/File:Pythag_anim.gif
Curiosità:
Il Teorema di Pitagora ammette una generalizzazione (citata da Euclide nei suoi Elementi): se su ciascun lato di un triangolo rettangolo costruiamo figure simili -ovvero tali che una sia l’ingrandimento o il rimpicciolimento di una delle altre- allora le loro aree soddisferanno la stessa relazione dei quadrati nel Teorema di Pitagora. Per esempio, consideriamo un triangolo rettangolo con dei triangoli simili costruiti sui cateti e sull’ipotenusa: