Con il suo Liber Abaci (1202), il matematico italiano Leonardo da Pisa detto Fibonacci fu uno dei primi studiosi a introdurre nel mondo occidentale il sistema numerico decimale (chiamato nel libro “modus indorum”, dato che fu utilizzato originariamente da matematici indiani). Oltre ad aver contribuito a questo fondamentale cambiamento nella storia della Matematica, in questo corposo trattato di aritmetica vengono studiate le proprietà delle quattro operazioni e alcune caratteristiche di numeri “particolari”, come i numeri perfetti o i numeri primi. Nel dodicesimo capitolo, Fibonacci introduce inoltre un metodo per ricavare una successione numerica: in seguito, questa successione verrà ricordata proprio con il nome di successione di Fibonacci.
La successione di Fibonacci nel Liber Abaci
Vediamo come, nel testo da lui scritto, Fibonacci introdusse la successione a lui intitolata.
Supponiamo di voler studiare come si evolve la popolazione di una colonia di conigli, costituita inizialmente da una sola coppia di conigli, che rispetti le seguenti condizioni:
- ogni coppia di conigli genera solamente un’altra coppia di conigli alla volta;
- i conigli hanno bisogno di un mese di vita per diventare fertili;
- una volta fertile, ogni coppia continuerà a generare una coppia di conigli al mese.
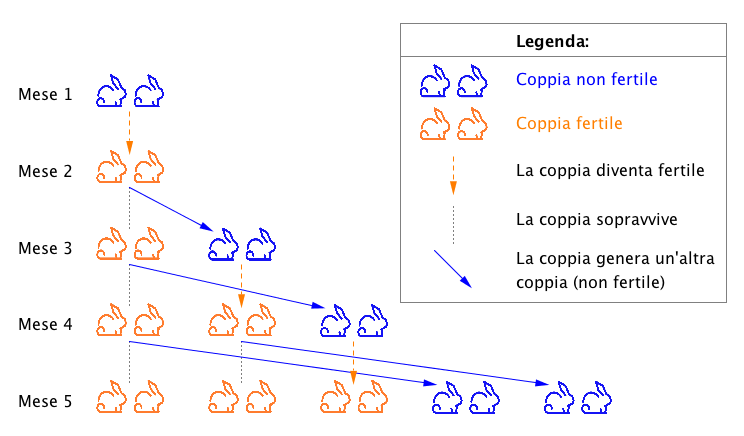
Ecco cosa accade alla popolazione della colonia dei conigli:
- Nel primo mese, abbiamo solo la coppia di partenza.
- Nel secondo mese, abbiamo nuovamente la coppia di partenza, che nel frattempo è diventata pronta a generare un’altra coppia di conigli.
- Nel terzo mese, la coppia di partenza ha generato una coppia di conigli, che non è ancora fertile. Quindi le coppie sono diventate $\mathbf{2}$ di cui una sola è fertile.
- Nel quarto mese, la coppia di partenza ha generato un’altra coppia di conigli. La coppia ottenuta al passo 3 è diventata fertile, ma non ha ancora generato un’altra coppia. Quindi le coppie ora sono $\mathbf{3}$, di cui $2$ fertili.
- Nel quinto mese, le due coppie fertili hanno generato un’altra coppia ciascuna. Quindi le coppie di conigli sono diventate $\mathbf{5}$; le due coppie appena nate non sono fertili, mentre le altre $3$ lo sono.
Riassumiamo questi cinque passaggi con la seguente illustrazione:
Potremmo andare avanti all’infinito con questo procedimento, ma quello che conta è rendersi conto di questo fatto fondamentale:
il numero di coppie di conigli al passo $n$, con $n\geq 3$, è uguale al numero di coppie di conigli al passo $n-1$ più il numero di coppie di conigli presenti al passo $n-2$.
Infatti:
- al passo $3$ le coppie sono $2$, che è proprio uguale al numero di coppie al passo $2$ (cioè una coppia) più il numero di coppie al passo $1$ (che è sempre una coppia);
- al passo $4$ le coppie sono $3$, che è uguale al numero di coppie al passo $3$ (cioè $2$ coppie) più il numero di coppie al passo $2$ (cioè $1$ coppia);
- al passo $5$ le coppie sono $5$, che è uguale al numero di coppie al passo $4$ (cioè $3$ coppie) più il numero di coppie al passo $3$ (cioè $2$ coppie);
e così via. Se elenchiamo in fila il numero di coppie di conigli presente in ciascun mese, otteniamo la successione: $$1, 1, 2, 3, 5, \ldots $$che prende il nome di successione di Fibonacci.
La successione di Fibonacci dal punto di vista matematico
Possiamo definire in maniera decisamente più astratta la successione vista prima, seguendo la definizione di successione numerica.
Consideriamo la successione $(f_n)_{n \in \mathbb{N}}$ definita nel seguente modo: $$ \begin{cases} f_1 = 1; \\ f_2 = 1; \\ f_n = f_{n-1} + f_{n-2} \quad n \geq 3 \end{cases}$$La successione $(f_n)_{n \in \mathbb{N}}$, come si dice con un termine tecnico, è definita per ricorsione. Se elenchiamo i suoi elementi otteniamo proprio la successione descritta da Fibonacci: $$1, 1, 2, 3, 5, 8, 13, 21, \ldots$$Infatti:
##KATEX##\begin{aligned}f_3 & = 2 = 1+1; \\f_4 & = 3 = 2+1; \\f_5 & = 5 = 3+2; \\f_6 & = 8 = 5+3; \\f_7 & = 13 = 8+5; \\f_8 & = 21 = 13+8; \\& \ \vdots\end{aligned}##KATEX##
Le proprietà della successione di Fibonacci
Questa successione numerica, la cui definizione è tutto sommato abbastanza semplice e intuitiva, gode di numerose proprietà. Elenchiamo qui le principali e le più curiose.
- Il rapporto tra due termini consecutivi della successione tende ad approssimare sempre meglio il rapporto aureo $\phi$. Infatti:
##KATEX##\begin{aligned}\frac{f_3}{f_2} & = 2; \\\frac{f_4}{f_3} & = \frac{3}{2} = 1,5;\\\frac{f_5}{f_4} & = \frac{5}{3} = 1,\overline{6};\\\frac{f_6}{f_5} & = \frac{8}{5} = 1,6; \\\frac{f_7}{f_6} & = \frac{13}{8} = 1,625;\\\frac{f_8}{f_7} & = \frac{21}{13} = 1, \overline{615384};\\& \ \vdots\end{aligned}##KATEX##
e $\phi = 1,618033 \ldots$. - Esiste una formula generale per ricavare il termine generico della successione di Fibonacci, a partire dal rapporto aureo $\phi$: $$f_n = \frac{\phi^n - ( - \phi)^{-n}}{\sqrt{5}}.$$
- La successione ottenuta considerando la somma dei termini presenti su ciascuna “diagonale” del triangolo di Tartaglia corrisponde proprio alla successione di Fibonacci.

Questa proprietà può essere riscritta facendo uso dei coefficienti binomiali: $$f_{n+1} = \sum_{k=1}^a \binom{n-k}{k}$$dove $a$ è il numero intero ottenuto approssimando per difetto $\frac{n}{2}$. - Per ogni $m, n, r \in \mathbb{N}$ opportuni, valgono le seguenti uguaglianze:
- Identità di Cassini: $$f_n^2 - f_{n-1} \cdot f_{n+1} = (-1)^{n-1}.$$
- Identità di Catalani: $$f_n^2 - f_{n-r} \cdot f_{n+r} = (-1)^{n-r} \cdot f_r^2.$$
- Identità di d’Ocagne: $$f_mf_{n+1} - f_{m+1}f_n = (-1)^nf_{m-n}.$$
Crediti immagini:
Rabbit Icon: created by Dream Icons from the Noun Project
"PascalTriangleFibanacci" by RDBury - Own work. Licensed under CC BY-SA 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:PascalTriangleFibanacci.svg#/media/File:PascalTriangleFibanacci.svg