Un sistema lineare può essere risolto utilizzando il metodo di sostituzione, o il metodo di riduzione, oppure il metodo del confronto. In questa lezione vedremo invece il metodo di Cramer e lo applicheremo ad alcuni esercizi per vedere come funziona.
Consideriamo un generico sistema di due equazioni lineari a due incognite. Effettuando alcune operazioni algebriche, possiamo sempre arrivare a scriverlo nella seguente forma:
##KATEX##\begin{cases}a_1x + b_1y = c_1 \\a_2x + b_2 y = c_2\end{cases}##KATEX##
dove $a_1, a_2, b_1, b_2, c_1, c_2$ sono numeri reali qualsiasi (l’unica condizione che poniamo, anche se non è strettamente necessaria, è che $a_1$ e $b_1$ oppure $a_2$ e $b_2$ non siano contemporaneamente uguali a $0$: altrimenti una delle due equazioni non conterrebbe le incognite).
Rappresentiamo questo sistema in una maniera diversa dal solito. Prendiamo tutti i coefficienti dei termini con le incognite $x$ e $y$ che sono presenti nelle due equazioni, e scriviamoli in una tabella, che di solito, viene chiamata matrice dei coefficienti: $$A = \left ( \begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix} \right ) $$Anche i termini noti $c_1$ e $c_2$ possono essere scritti in una tabella che, di solito, viene chiamata vettore dei termini noti: $$c = \left ( \begin{matrix} c_1 \\ c_2 \end{matrix} \right ) $$Possiamo dunque dire che avere a che fare con un sistema lineare di due equazioni a due incognite è come trattare con una matrice $A$ con due righe e due colonne (che contiene quindi quattro numeri), e con un vettore $c$ con due righe (che contiene quindi due numeri).
Definizione
Consideriamo un sistema di due equazioni lineari a due incognite con matrice dei coefficienti $A$. Il determinante del sistema è il numero $$D = a_1b_2 - a_2b_1$$Spesso si dice anche che $D$ è il determinante della matrice dei coefficienti $A$.
A volte il determinante della matrice $A$ si scrive nel seguente modo: $$D = det(A) = \left | \begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix} \right | $$Inoltre, un modo abbastanza comodo per ricordarsi come si calcola il determinante è il seguente:
- moltiplicare gli elementi presenti sulla diagonale della tabella che parte da in basso a destra (fare cioè $a_1 \cdot b_2$);
- moltiplicare gli elementi presenti sulla diagonale della tabella che parte da in basso a sinistra (fare cioè $a_2 \cdot b_1$);
- sottrarre il secondo numero al primo.

Definizione
Consideriamo un sistema di due equazioni lineari a due incognite con matrice dei coefficienti $A$ e vettore dei termini noti $c$. Si chiama determinante dell’incognita $x$, e lo indichiamo con $D_x$, il determinante della matrice $A_x$ ottenuta sostituendo in $A$ la colonna dei coefficienti dei termini della $x$ con il vettore dei termini noti $c$ (rispettando l’ordine delle equazioni). In formule:
##KATEX##\begin{aligned}A_x & = \left ( \begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}##KATEX## \right )\\
D_x = det (A_x) & = \left | ##KATEX##\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}##KATEX## \right | = c_1b_2 - c_2b_1
\end{aligned}
In maniera analoga possiamo definire il determinante dell’incognita $y$: $$D_y = det (A_y) = \left | \begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix} \right | = a_1c_2 - a_2c_1$$
Tutte queste definizioni trovano utilità nella regola di Cramer, che enunciamo qui sotto.
Consideriamo un sistema di due equazioni lineari a due incognite, con matrice dei coefficienti $A$ e vettore dei termini noti $c$. Allora il sistema è determinato (cioè, ammette una sola soluzione) se e solo se il determinante $D$ del sistema è diverso da zero. In questo caso, la soluzione del sistema è la coppia $(x, y) = (a, b)$ data da: $$a = \frac{D_x}{D}, \quad b = \frac{D_y}{D}$$dove $D_x$ e $D_y$ sono i determinanti dell’incognita $x$ e $y$ rispettivamente.
Se il determinante $D$ è invece uguale a zero, il sistema può essere alternativamente impossibile (cioè, non ammette alcuna soluzione) o indeterminato (cioè, ammette infinite soluzioni). La prima situazione si verifica quando sia $D_x$ che $D_y$ sono diversi da zero, mentre se almeno uno tra $D_x$ e $D_y$ si annulla allora il sistema è indeterminato.
Proviamo ad applicare questa regola al sistema:
##KATEX##\begin{cases}2x - y = 3 \\3x + 2y = 1\end{cases}##KATEX##
Scriviamo la matrice dei coefficienti e il vettore dei termini noti: $$ A = \left ( \begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix} \right ) = \left ( \begin{matrix} 2 & -1 \\ 3 & 2 \end{matrix} \right ) \quad c = \left ( \begin{matrix} c_1 \\ c_2 \end{matrix} \right ) = \left ( \begin{matrix} 3 \\ 1 \end{matrix} \right ) $$Il determinante del sistema è $D = a_1b_2 - a_2b_1 = 2 \cdot 2 - 3 \cdot (-1) = 4 + 3 = 7$. Dato che $D \neq 0$, il sistema è determinato.
I determinanti delle incognite sono:
##KATEX##\begin{aligned}D_x & = \left | \begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}##KATEX## \right | = \left | ##KATEX##\begin{matrix} 3 & -1 \\ 1 & 2 \end{matrix}##KATEX## \right | = 3 \cdot 2 - 1 \cdot (-1) = 6 + 1 = 7 \\
D_y & = \left | ##KATEX##\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}##KATEX## \right | = \left | ##KATEX##\begin{matrix} 2 & 3 \\ 3 & 1 \end{matrix}##KATEX## \right | = 2 \cdot 1 - 3 \cdot 3 = 2 -9 = -7
\end{aligned}
e quindi per la regola di Cramer l’unica soluzione $(a, b)$ del sistema è data da: $$a = \frac{D_x}{D} = \frac{7}{7} = 1, \qquad b = \frac{D_y}{D} = \frac{-7}{7} = -1$$In effetti si verifica facilmente che, risolvendo questo sistema con il metodo di sostituzione o di riduzione, la soluzione è proprio questa; o più semplicemente si può sostituire $a$ al posto di $x$ e $b$ al posto di $y$ per verificare che entrambe le equazioni del sistema sono soddisfatte.
Quali sono i pro e i contro del metodo di Cramer?
PRO:
- si può utilizzare per capire in fretta se il sistema è determinato.
- come vedremo nel prossimo paragrafo, è generalizzabile in maniera naturale a sistemi con $n$ equazioni e $n$ incognite.
- una volta che si ha familiarità con le formule, è abbastanza rapido.
CONTRO:
- non molto semplice da memorizzare quando si affronta per la prima volta.
- all'aumentare delle equazioni e delle incognite, i calcoli diventano molto lunghi (vedi prossimo paragrafo).
- quando il determinante del sistema è zero, bisogna fare un'analisi separata (con un altro metodo) per capire se il sistema è indeterminato o impossibile.
Regola di Cramer per sistemi con $n$ equazioni lineari a $n$ incognite
La regola di Cramer, che abbiamo visto applicata a un sistema di due equazioni lineari a due incognite, può essere riformulata per risolvere un sistema di $n$ equazioni lineari a $n$ incognite. È infatti possibile definire un determinante $D$ anche per un sistema di questo tipo, a partire dalla sua matrice dei coefficienti (che avrà $n$ righe e $n$ colonne); in maniera analoga a quanto fatto prima, inoltre, si possono definire i determinanti $D_{x_1}, D_{x_2}, \ldots D_{x_n}$ di ciascuna delle $n$ incognite. Se $D \neq 0$, la soluzione del sistema è unica ed è la $n$-upla $(z_1, z_2, \ldots z_n)$ data da: $$z_1 = \frac{D_{x_1}}{D}, \quad z_2 = \frac{D_{x_2}}{D}, \quad \ldots \quad z_n = \frac{D_{x_n}}{D}$$in perfetta analogia con quello che abbiamo fatto per due equazioni lineari a due incognite.
L’espressione per il determinante di una matrice con $n$ righe e $n$ colonne è, però, molto complicata. Ci limiteremo solo ad analizzare il caso appena più complicato rispetto a quanto fatto nella sezione precedente, e cioè il caso $n = 3$.
Consideriamo allora un sistema di $3$ equazioni lineari in $3$ incognite:
##KATEX##\begin{cases}a_1x + b_1y + c_1z = d_1 \\a_2x + b_2y + c_2z = d_2 \\a_3x + b_3y + c_3z = d_3\end{cases}##KATEX##
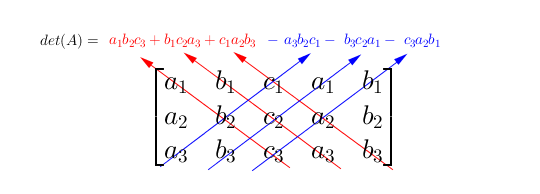
In questo caso la matrice dei coefficienti $A$ e il vettore dei termini noti $d$ sono: $$ A = \left ( \begin{matrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{matrix} \right ), \qquad d = \left ( \begin{matrix} d_1 \\ d_2 \\ d_3 \end{matrix} \right ) $$Il determinante della matrice $A$, o meglio, di una qualsiasi matrice con $3$ righe e $3$ colonne, è dato dalla seguente formula (di cui non forniamo né una motivazione né una dimostrazione): $$det(A) = a_1b_2c_3 + b_1c_2a_3 + a_2b_3c_1 - c_1b_2a_3 - c_2b_3a_1 - a_2b_1c_3$$Possiamo ricordare abbastanza facilmente questa formula con un “trucco”: la Regola di Sarrus. Questa regola consiste in:
- riscrivere le prime due colonne della matrice $A$ a fianco di $A$ stessa;

- considerare le diagonali evidenziate in figura:

- moltiplicare fra loro i numeri collegati dalle linee che abbiamo tracciato e sommare i risultati che abbiamo ottenuto, mettendo un segno meno davanti alle moltiplicazioni che derivano dalle diagonali in blu.
Proseguiamo con la risoluzione del sistema. In maniera del tutto analoga a quanto fatto prima per due equazioni a due incognite, costruiamo le matrici $A_x, A_y, A_z$:
##KATEX##\begin{aligned}A_x & = \left ( \begin{matrix} d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3 \end{matrix}##KATEX## \right ) \\
A_y & = \left ( ##KATEX##\begin{matrix} a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3 \end{matrix}##KATEX## \right ) \\
A_z & = \left ( ##KATEX##\begin{matrix} a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3 \end{matrix}##KATEX## \right )
\end{aligned}
Possiamo quindi trovare i determinanti dell’incognita $D_x, D_y, D_z$. Se $D \neq 0$, il sistema ha una sola soluzione $(a, b, c) = \left ( \frac{D_x}{D}, \frac{D_y}{D}, \frac{D_z}{D} \right )$.
Facciamo un esempio. Consideriamo il sistema:
##KATEX##\begin{cases}3x+ & & 2z &=1 \\& y & -z & =3 \\x & +y &+z & =2\end{cases}##KATEX##
Il modo in cui abbiamo scritto il sistema rende più facile la compilazione della matrice dei coefficienti $A$ e del vettore dei termini noti $d$: $$ A = \left ( \begin{matrix} 3 & 0 & 2 \\ 0 & 1 & -1 \\ 1 & 1 & 1 \end{matrix} \right ), \qquad d = \left ( \begin{matrix} 1 \\ 3 \\ 2 \end{matrix} \right ) $$Allora:
##KATEX##\begin{aligned}D & = 3 \cdot 1 \cdot 1 + 0 \cdot (-1) \cdot 1 + 2 \cdot 0 \cdot 1 - 2 \cdot 1 \cdot 1 - 3 \cdot (-1) \cdot 1 - 0 \cdot 0 \cdot 1 = \\& = 3 + 0 + 0 - 2 + 3 - 0 = 4\end{aligned}##KATEX##
Siccome $D \neq 0$, il sistema ha una sola soluzione. Si può verificare che $D_x = 4, D_y = 8, D_z = -4$ e quindi che la soluzione di questo sistema è la terna $(a, b, c) = \left ( \frac{4}{4}, \frac{8}{4}, \frac{-4}{4} \right ) = (1, 2, -1)$.
Revisione scientifica a cura di Marco Guglielmino