Quando vogliamo calcolare l’area o il perimetro di un poligono (come un triangolo, o un quadrilatero) utilizziamo formule specifiche a seconda dell’oggetto geometrico che stiamo considerando. In questa lezione elenchiamo le formule principali per determinare alcune grandezze relative a una circonferenza e al cerchio che essa determina.
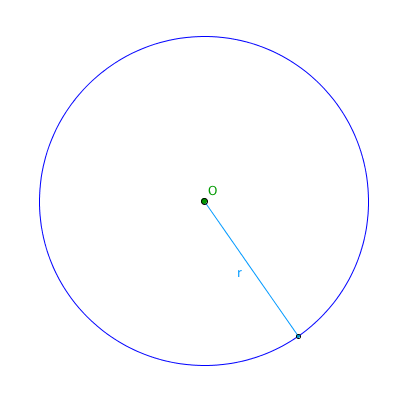
Per una circonferenza con raggio di misura $r$, abbiamo:
Lunghezza della circonferenza: $C = 2 \pi r$
Area del cerchio: $A = \pi r^2$
Raggio: $r = \frac{C}{2 \pi} = \sqrt{\frac{A}{\pi}}$
Diametro: $d = 2r$
Consideriamo ora il seguente disegno:

Utilizzando la definizione di radiante, e supponendo che l’angolo al centro $\alpha$ sia espresso in radianti, possiamo determinare la misura dell’arco $\overset{\frown}{AB}$ in questo modo: $$\overset{\frown}{AB} = \alpha \cdot r.$$ L’area del settore circolare è invece così determinata: $$Area(AOB) = \frac{1}{2} r^2 \alpha = \frac{1}{2}r \cdot \overset{\frown}{AB}.$$
Inoltre, utilizzando la funzione trigonometrica $\sin(x)$, è possibile ricavare la lunghezza della corda $AB$: $$AB = 2r \sin \left ( \frac{\alpha}{2} \right ) = d \sin \left ( \frac{\alpha}{2} \right ).$$
Revisione scientifica a cura di Marco Guglielmino