Equazioni e disequazioni parametriche irrazionali

Una equazione parametrica irrazionale è un’uguaglianza tra due espressioni letterali in cui compare l’incognita, di solito indicata dalla lettera $x$, sotto il segno di radice, o elevata ad un esponente frazionario, e in cui, inoltre sono presenti, oltre all’incognita, altre lettere, indicate come parametri dell’equazione. Ad esempio, ##KATEX##\begin{aligned}\sqrt{x^3 - a} = 3 \\ \sqrt{a}= \sqrt[3]{x} + ax \\ \sqrt[3]{ax} \sqrt{a-x} = 1\end{aligned}##KATEX##sono tutte equazioni parametriche irrazionali. 
Le disequazioni parametriche irrazionali presentano un segno di disuguaglianza al posto del $=$, ossia $<$, $>$, $\leq$ o $\geq$. 

Il procedimento da seguire per risolvere questa tipologia di equazioni o disequazione ricalca totalmente quello già illustrato per le equazioni irrazionali o le disequazioni irrazionali, rispettivamente, senza i parametri. Lo scopo è sempre quello di trovare la soluzione dell’equazione o disequazione, ossia quell’insieme di valori che l’incognita può assumere per rendere vera l’equazione o la disequazione. La complicazione, nel caso siano presenti parametri, giunge quando le soluzioni trovate debbono essere confrontate con le (eventuali) condizioni di esistenza: in questo caso si parla di condizioni di accettabilità delle soluzioni. Possiamo riassumere il procedimento generale nei seguenti punti:  

1. Porre le condizioni di esitenza quando si è in presenza di radicali di ordine pari. Dalla definizione di radicale, è necessario che l’argomento di una radice pari sia maggiore o uguale a zero. 
2. Se possibile, isolare il radicale da un lato dell’equazione o disequazione. Questo passo può richiedere svariati passaggi algebrici, che sfruttano necessariamente tutte le proprietà dei radicali. 
3. Risolvere l’equazione irrazionale o la disequazione irrazionale con l’usuale metodo di risoluzione. Si giungerà così ad una soluzione, che però indichiamo come provvisoria: infatti, questa soluzione, in generale, dipende dai parametri. Questo porta ad una discussione sull’accettabilità di dette soluzioni, da svolgere nel prossimo punto.
4. La soluzione provvisoria ottenuta al punto precedente deve essere confrontata con le condizioni di esistenza ottenute al punto 1: eventuali soluzioni che entrano in conflitto con le condizioni di esistenza devono essere scartate. Queste condizioni aggiuntive sulla forma delle soluzioni vengono dette condizioni di accettabilità della soluzione. Siccome le soluzioni di problemi di questo tipo possono risultare alquanto complicate, nella loro forma, si consiglia di riassumerle sempre, mettendo bene in evidenza i valori ammissibili dell’incognita al variare di quelli del parametro in uno schema riassuntivo.  

Alcune esempi serviranno a fissare le idee. Sottolineamo che per risolvere tali esercizi serve avere una certa familiarità con le controparti senza parametri, cioè con equazioni e disequazioni irrazionali, nonchè con i radicali in genere: il processo è comunque analogo a quello che si affronta quando occorre risolvere equazioni o disequazioni letterali fratte. 

Esempio 1 

Risolvere l’equazione$$ \frac{\sqrt{1 + \frac{x}{a}} + \sqrt{1 - \frac{x}{a}}}{\sqrt{1 + \frac{x}{a}} - \sqrt{1 - \frac{x}{a}}} = \frac{a}{x} $$L’incognita è la lettera $x$, mentre la lettera $a$ è da considerarsi un parametro. 

1. Poniamo le condizioni di esistenza. Innanzitutto, le frazioni algebriche hanno significato solo quando i denominatori sono diversi da zero: poniamo quindi $x \neq 0, a \neq 0$. Inoltre, i due radicali prescrivono che $1 - \frac{x}{a} \geq 0$ e che $1 + \frac{x}{a} \geq 0$: dopo semplici passaggi algebrici, si giunge alle condizioni $x \geq -a$ e $x \leq a$, che possono essere riassunte in $-a \leq x \leq a$. Le condizioni di esistenza sono quindi$$-a \leq x \leq a, x \neq 0 \text{ e } a \neq 0$$ 
2. Manipoliamo algebricamente l’equazione nel tentativo di isolare un radicale. Notiamo che la frazione può essere razionalizzata moltiplicando sopra e sotto per $\sqrt{1 + \frac{x}{a}} + \sqrt{1 - \frac{x}{a}}$: così facendo, si arriva all’equazione$$ \frac{\left(\sqrt{1 + \frac{x}{a}} + \sqrt{1 - \frac{x}{a}}\right)^2}{\sqrt{1 + \frac{x}{a}} - \sqrt{1 - \frac{x}{a}}} = \frac{a}{x}$$Eseguiamo le operazioni indicate:##KATEX##\begin{aligned}\frac{1 + \frac{x}{a} + 2 \sqrt{1 - \frac{x^2}{a^2}} + 1 - \frac{x}{a}}{2 \frac{x}{a}} = \frac{a}{x} \\2 + 2 \sqrt{1 - \frac{x^2}{a^2}} = 2 \\2 \sqrt{1 - \frac{x^2}{a^2}} = 0 \end{aligned}##KATEX## 
   Avendo isolato un radicale, possiamo passare al punto successivo. 
3. Ora siamo di fornte ad un’equazione irrazionale e possiamo seguire il normale procedimento. Otteniamo che le soluzioni dell’equazione di partenza sono necessariamente le soluzioni di $1 - \frac{x^2}{a^2} = 0$, ossia $x^2 = a^2$. Questa è un’equazione parametrica di secondo grado, le cui soluzioni sono $x = \pm a$. 
4. Confrontiamo le soluzioni ottenute al punto 3 con le condizioni di esistenza di cui al punto 1: innanzitutto, $x = \pm a$ è sempre compatibile con $-a \leq x \leq a$. Tuttavia, le soluzioni $x = \pm a$ non escludono il caso $x = 0$: anzi, se $a=0$, in quelle soluzioni, implica proprio $x=0$. Ma siamo fortunati, perchè il valore del parametro $a=0$ non è accettabile, per le condizioni di esistenza: per $a=0$ l’equazione è quindi priva di significato. La soluzione, in definitiva, è la seguente$$ \begin{cases} \text{se } a =0 & \text{ l’equazione è priva di significato} \\ \text{se } a \neq 0 & x = \pm a \end{cases}$$ 

Esempio 2 
 
Risolvere la disequazione irrazionale$$ \sqrt{(a-1)x + 2-a} \leq x$$Il parametro è la lettera $a$, mentre l’incognita è rappresentata dalla $x$. 

1. Poniamo le condizioni di esistenza $(a-1)x + 2-a \geq 0$. Nel caso in cui $a = 1$, la condizione diventa $1 \geq 0$, che è sempre verificata. Se $a > 1$, abbiamo che $a-1 > 0$, e quindi le condizioni di esistenza diventano $$ x \geq \frac{a-2}{a-1}$$Se invece $a < 1$, $a-1 <0$ e quindi il segno della disequazione cambia: le condizioni di esistenza sono$$ x \leq \frac{a-2}{a-1}$$ 
2. Non c’è bisogno di manipolare la disequazione per isolare il radicale: almeno da questo punto di vista, i calcoli sono facili. 
3. Procediamo a risolvere la disequazione come se fosse una normale disequazione irrazionale. Siccome essa si presenta nella forma $\sqrt{P(x)} \leq Q(x)$, fermo restanti le condizioni di esistenza, le soluzioni sono tutte e sole quelle del sistema $\begin{cases} Q(x) \geq 0 \\ P^2(x) \leq Q(x) \end{cases}$, o, nel nostro caso, $$ \begin{cases} x \geq 0 \\ (a-1)x + 2-a \leq x^2 \end{cases}$$La seconda disequazione, che manipolata algebricamente risulta essere $x^2 + (1-a)x -2 +a \geq 0$, è una disequazione parametrica di secondo grado. Il suo delta, che compare nella formula risolutiva, è pari a $(a-3)^2$, il che ci impone di trattare il caso $a=3$ separatamente. Se dunque $a \neq 3$, abbiamo due soluzioni distinte in $x_0 = 1$ e $x_a = a-2$. Bisogna prestare attenzione a come sono disposte queste due soluzioni l’una rispetto all’altra: se $a<3$, $x_0 > x_a$, mentre se $a>3$ abbiamo $x_a > x_0$. Dividiamo nei seguenti casi: 
   • $a<1$: in questo caso, la soluzione di $x^2 + (1-a)x -2 +a \geq 0$ è $x > x_0 =1 \ \vee x < x_a = a-2$, ma essendo $a<1$, sicuramente $x_a<0$, il che confligge con la prima disequazione del sistema: abbiamo il seguente schema 
     
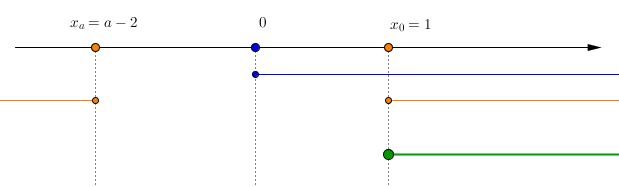
     Si evince facilmente che la soluzione, in questo caso, è $x \geq 1$ 
   • $a=1$: per questo particolare valore del parametro, la disequazione diventa $ 1 \leq x$, che ha come soluzione ancora $x \geq 1$. 
   • $1<a < 2$: anche in questo caso si perviene alla soluzione $x \geq 1$: abbiamo uno schema del tutto analogo al precedente. 
   • Per $a = 2$ abbiamo un caso particolare, dal momento che $x_a = 0$: alla soluzione $x \geq 1$ occorre aggiungere anche $x = 0$, dato che se $x=0$ vale sia $x \geq 0$ sia $x \leq x_a$. 
   • Per $2 < a < 3$ invece abbiamo una situazione differente: la radice $x_a$ viene a situarsi dopo lo zero. Dunque il diagramma è simile a questo: 
     
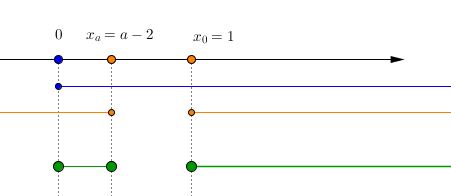
   • Come preannunciato, per $a = 3$ abbiamo un caso a parte: per questo valore del parametro, la disequazione diventa $\sqrt{2x -1 } \leq x$, da cui ci si riconduce al sistema $\begin{cases} x \geq 0 \\ x^2 -2x +1 \geq 0 \end{cases}$, che è soddisfatto per ogni valore di $x$ reale. 
   • Infine abbiamo $a > 3$. In questo caso, l’ordinamento di $x_0$ e $x_a$ si scambia, e otteniamo dunque la soluzione $0<x<x_0 \ \vee \ x>x_a$: 
     
4. Ora che abbiamo scoperto delle provvisorie soluzioni per tutti i possibili valori del parametro $a$, è necessario intersecare ciascuna di queste con le relative condizioni di esistenza. Per $a<1$, esse sono $x \leq \frac{a-2}{a-1}$, mentre per $a > 1$ deve essere $x \geq \frac{a-2}{a-1}$. Dobbiamo quindi prestare particolarmente attenzione a dove si collochi il valore $\frac{a-2}{a-1}$ rispetto agli altri valori coinvolti nella disequazione: nello specifico, $0$, $1$ e $a-2$. Intersecando queste condizioni con le soluzioni provvisorie trovate al punto precedente, arriviamo alla soluzione della disequazione di partenza:$$ \begin{cases} & \text{Se } a < 1 & 1 \leq x \leq \frac{a-2}{a-1} \\& \text{se } 1 \leq a < 2 & x \geq 1 \\& \text{se } a = 2 & x = 0 \ \vee \ x \geq 1 \\ & \text{se } 2 < a < 3 & \frac{a-2}{a-1} \leq x \leq a-2 \ \vee \ x \geq 1 \\& \text{se }a = 3 & x \geq \frac{1}{2} \\& \text{se }a > 3 & \frac{a-2}{a-1} \leq x \leq 1 \vee x \geq a-2 \end{cases}$$