La legge di Faraday prescrive che in presenza di un campo magnetico il cui flusso attraverso un circuito non sia costante nel tempo, si generi nel circuito una forza elettromotrice (e quindi, per le leggi di Ohm, una corrente elettrica) nel circuito stesso. Più precisamente, se in un intervallo di tempo di durata $\Delta t$ si registra una variazione di flusso magnetico $\Delta \Phi (\vec{B})$, la forza elettromotrice (o f.e.m.) indotta nel circuito ha un’intensità di$$ \mathscr{E} = \frac{\Delta \Phi (\vec{B})}{ \Delta t }$$Sebbene lo stesso Faraday avesse illustrato ampiamente il verso della corrente indotta dalla legge che porta il suo nome, la legge stessa non reca, nella sua espressione, alcuna traccia di quest’aspetto.
Una trattazione generale della questione venne successivamente svolta da Emilij Lenz, un fisico Estone che negli anni ‘30 e ‘40 del 1800 si occupò di elettromagnetismo. Egli precisò ulteriormente la legge di Faraday, arrivando a una formulazione più completa.
Enunciato
La legge di Lenz afferma che la forza elettromotrice indotta in un circuito genera una corrente, detta corrente indotta, il cui effetto deve essere tale da opporsi alla causa che la produce. Si può riassumere l’enunciato in una formula, del tutto analoga alla legge di Faraday: $$ \mathscr{E} = - \frac{\Delta \Phi (\vec{B})}{ \Delta t }$$A onore del lavoro dei fisici che la scoprirono, la formula precedente è anche nota sotto il nome di Legge di Faraday-Lenz. Il significato di questa opposizione è da ricercarsi nella terza legge della dinamica, o principio di azione-reazione, e nella legge di conservazione dell’energia: sollecitato dal flusso magnetico, un circuito genera a sua volta, mediante una circolazione di carica elettrica (cioè una corrente) un campo magnetico per contrastare l’azione che subisce, uguale in modulo ma contrario in verso.
Chiariamo l’enunciato con alcuni esempi.
Ricordiamo innanzitutto che la corrente passante in un circuito elettrico genera a sua volta un campo magnetico, detto campo magnetico indotto, secondo la legge di Oersted o la legge di Biot-Savart. Il significato preciso della legge di Faraday-Lenz, dunque, è il seguente: se il campo magnetico variabile $\vec{B}$ induce in un circuito una corrente $i$, la circolazione di tale corrente deve indurre a sua volta un campo magnetico $\vec{B}’$ in verso opposto al campo $\vec{B}$ che l’ha indotta. L’illustrazione seguente rende conto di tale fatto:
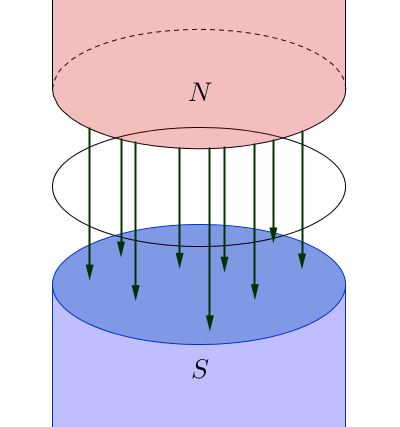

Possiamo anche considerare il seguente esempio. Si supponga di disporre di due spire: la prima costituita seplicemente da un filo conduttore chiuso su se stesso, la seconda collegata ad un generatore, inizialmente spento. Si faccia riferimento alla figura seguente.

Accendiamo il generatore: la corrente elettrica circolante raggiungerà il suo valore limite $i$ (dato dalla prima legge di Ohm, $i = V / R$, dove $V$ è la d.d.p. prodotta dal generatore, ed $R$ è la resistenza del conduttore) in un intervallo di tempo di durata $\Delta t$ (molto molto breve). Questo incremento di corrente (da $0$ a $i$) genera un campo magnetico $\vec{B}$, che, nel caso in esame, è orientato dal basso verso l’alto. Questo campo passa attraverso la prima spira, e dunque induce una corrente $i’$ il cui verso deve essere tale da generare un campo magnetico $\vec{B}’$ che si oppone alla creazione del campo $\vec{B}$: $\vec{B}’$ sarà rivolto dall’alto verso il basso, e quindi la corrente $i’$ circolerà in verso opposto ad $i$.
Concludiamo con un esempio numerico.
Esercizio
Una bobina quadrata di lato $10 \text{ cm}$ è costituita da 20 spire compatte di resistenza complessiva di $7 \Omega$. La bobina si trova disposta su un piano perpendicolare ad un campo magnetico, la cui intensità viene fatta variare nel tempo secondo la relazione$$ B = B_0 + \beta \ t, $$ove $B_0$ è l’intensità iniziale, pari a $2.5 \cdot 10^{-1} \text{ T}$, $t$ è il tempo misurato in secondi $\text{s}$, e $\beta$ è una costante di proporzionalità pari a $2 \cdot 10^{-2} \text{ T}/\text{s}$. Determinare il valore dell’intensità di corrente che si produce nella bobina.
Svolgimento
Per la legge di Faraday-Lenz sappiamo che $\mathscr{E} = - \frac{\Delta \Phi (\vec{B})}{ \Delta t }$; il flusso del campo magnetico attravesro la spira, essendo il campo perpendicolare alla spira, è semplicemente il prodotto tra intensità del campo $B$ e area della spira $S$, non dimenticando che sono presenti $n = 20$ spire: il flusso sarà dunque pari a $\Phi (\vec{B}) = n \ S \ B = nS\ (B_0 + \beta \ t)$. Supponiamo che trascorra un intervallo di tempo di durata $\Delta t$: essendo i valori $n$, $S$ e $B_0$ costanti, la variazione di flusso magnetico sarà pari a $$ \Delta \Phi (\vec{B}) = \Delta \left( nS\ (B_0 + \beta \ t) \right) = \underbrace{\Delta \left( nS\ B_0 \right)}_{\text{costante} \Rightarrow \Delta(\dots) = 0} + \Delta \left( nS\beta \ t \right) = nS \beta \Delta t $$Per la legge di Lenz allora la forza elettromotrice indotta è $$ \mathscr{E} = -\frac{nS \beta \Delta t }{\Delta t} = -nS \beta$$dove il segno $-$ sta a indicare il fatto che la corrente circolerà nel verso tale per cui il campo magnetico da essa indotto si opponga al campo generatore $\vec{B}$. Per la prima legge di Ohm, l’intensità di corrente è data dal rapporto tra differenza di potenziale agli estremi del generatore, che in valore è pari ad $\mathscr{E}$, e la resistenza $R$: $$ i = \frac{\mathscr{E}}{R} = \frac{nS \beta}{R} $$L’area $S$ è l’area di un quadrato di lato $10^{-1} \text{ m}$, ed è dunque pari a $10^{-1} \cdot 10^{-1} = 10^{-2} \text{ m}^{2}$. Sostituendo nella formula i dati numerici in nostro possesso, si ottiene una corrente di intensità pari a $$ i = \frac{20 \cdot 10^{-2} \cdot 2 \ 10^{-2}}{7 \Omega} = 5.7143 \cdot 10^{-4} \text{ A}$$