Sappiamo che un filo conduttore percorso da corrente elettrica costante genera un campo magnetico: lo scoprì, quasi per caso, il fisico danese Hans Christian Ørsted, con un famoso esperimento.
La rappresentazione del campo magnetico intuitivamente più efficace è quella che utilizza le linee di campo: queste linee possono essere visualizzate grazie alle proprietà magnetiche della limatura di ferro, che si dispone naturalmente secondo il campo magnetico, dato che ogni minuscola scheggia di ferro funge da ago magnetico. Nella figura sottostante, della limatura di ferro è stata posto attorno ad un filo elettrico, posto al centro, in cui viene fatta scorrere della corrente.

Come vediamo, le linee di campo sembrano essere delle circonferenze concentriche, che hanno come centro proprio il cavo elettrico. Intuiamo quindi che la direzione del campo magnetico $\vec{B}$ debba essere tangente a queste circonferenze; ma essendo $\vec{B}$ un vettore, ci occorono ancora le infomrazioni sul suo modulo ed il suo verso per descriverlo correttamente.
Attorno al 1820, i fisici francesi Jean-Baptiste Biot e Félix Savart svolsero numerosi studi e riuscirono a formulare, dopo ampie verifiche sperimentali, quella che oggi va sotto il nome di legge di Biot-Savart: serve a determinare il campo magnetico $\vec{B}$ prodotto in un punto dello spazio da un filo rettilineo percorso da corrente elettrica. Essa afferma quanto segue.
Si consideri un filo rettilineo, percorso da corrente di intensità $I$, e ci si ponga in un punto $P$ nello spazio, posto ad una distanza $r$ dal filo. Allora in $P$ è presente un campo magnetico $\vec{B} = \vec{B}(P)$ dotato di:
- Modulo dato dalla seguente formula:$$ B = \frac{\mu_0}{2 \pi}\frac{I}{r}$$Il simbolo $\mu_0$, che si legge “my zero” (la my è una lettera dell’alfabeto greco che sta per m), è una costante detta permeabilità magnetica del vuoto, ed il suo valore in unità del sistema internazionale è $4 \pi \cdot 10^{-7} = 1.25663706144... \cdot 10^{-6} \text{V s}\text{ A}^{-1}$.
- Direzione individuata dalla retta tangente alla circonferenza di raggio $r$ passante per $P$, giacente nel piano perpendicolare al filo e passante per $P$.
- Verso indicato dalla regola della mano destra: se indichiamo con il pollice della mano destra il verso di percorrenza della corrente all’interno del filo e chiudiamo le altre dita sul palmo, avremo il verso in cui punta $\vec{B}$. La figura seguente vale più di mille parole:

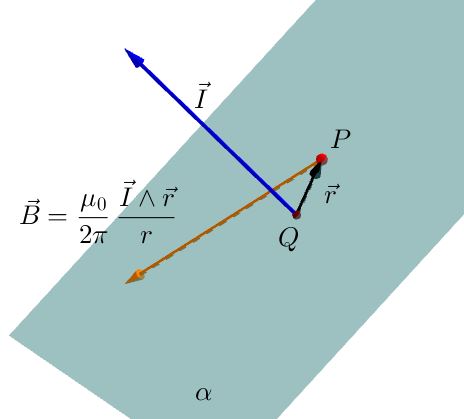
Si può riassumere il tutto facendo ricorso all’uso del prodotto vettore. Consideriamo il piano perpendicolare al filo e che passa per $P$: questo piano lo chiamiamo $\alpha$, ed il punto in cui esso interseca il filo lo battezziamo $Q$. Indichiamo con $\vec{r}$ il vettore $\overrightarrow{QP}$, e con $\vec{I}$ il vettore di piede $Q$, direzione del filo, verso concorde con quello della corrente e modulo pari all’intensità di corrente $I$. Con queste definizioni ausiliarie possiamo condensare la legge di Biot-Savart in una sola formula:$$ \vec{B} = \frac{\mu_0}{2 \pi} \frac{\vec{I} \wedge \vec{r}}{r}$$
Crediti immagini:
https://commons.wikimedia.org/wiki/File:PSM_V56_D0072_Magnetic_whirls_around_the_sending_wire.png
Jfmelero https://commons.wikimedia.org/wiki/File:Manoderecha.svg