La proprietà invariantiva è una delle proprietà delle quattro operazioni; le altre proprietà che di solito vengono studiate sono le proprietà commutativa, distributiva, associativa e dissociativa. A differenza delle altre proprietà appena elencate, la proprietà invariantiva riguarda esclusivamente le operazioni di divisione e sottrazione.
Proprietà invariantiva della sottrazione: In una sottrazione, se aggiungiamo o togliamo la stessa quantità al minuendo e al sottraendo, il risultato finale (cioè, la differenza) non cambia.
Vediamo subito un esempio. Prendiamo la sottrazione $$17 - 9 = 8$$In questo caso il minuendo è $17$, il sottraendo è $9$ e la differenza è $8$. Proviamo ad aggiungere $1$ sia a minuendo che al sottraendo:

Si vede che la sottrazione ottenuta ha lo stesso risultato della precedente: nonostante minuendo e sottraendo siano cambiati, la differenza è rimasta invariata.
Per completezza, facciamo anche un esempio in cui sottraiamo lo stesso numero (nel nostro caso $4$) a minuendo e sottraendo:

Anche qui la differenza è invariata, il che mostra la validità della proprietà invariantiva della sottrazione.
Proprietà invariantiva della divisione: In una divisione, se dividiamo o moltiplichiamo dividendo e divisore per la stessa quantità, il risultato finale (cioè, il quoziente) non cambia.
Prendiamo immediatamente un esempio pratico: consideriamo la divisione $$60:12 = 5$$Il dividendo è $60$, il divisore è $12$, mentre il quoziente è $5$. Moltiplichiamo per $5$ dividendo e divisore:
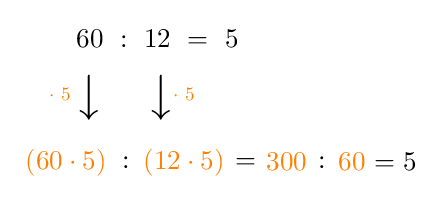
Il risultato della divisione è invariato: rimane cioè sempre $5$.
Anche se dividiamo $60$ e $12$ per lo stesso numero, per esempio $6$, otteniamo lo stesso quoziente:

Osservazioni sulla proprietà invariantiva
A cosa serve la proprietà invariantiva? Oltre a essere interessante in quanto tale, questa proprietà può essere sfruttata per svolgere alcuni conti in maniera “comoda”.
- Dopo aver aggiunto $1$ a entrambi i membri della sottrazione del nostro esempio, trovare la differenza è molto più semplice (basta “togliere” il numero $1$ davanti all’$8$, dato che il sottraendo è $10$).
- Quando abbiamo applicato la proprietà invariantiva della divisione, dividendo il divisore e il dividendo per $6$, siamo riusciti a ottenere una divisione la cui risoluzione può essere ricondotta solamente all’uso delle tabelline!
Quello che abbiamo appena detto ci fa capire che in molti casi un uso adeguato della proprietà invariantiva può portare a conti più semplici da svolgere. Difficilmente però possiamo dare una regola generale da seguire: sarà l’esperienza e i tanti esercizi a far capire se è il caso o meno di applicare questa proprietà, e come applicarla.
È importante notare che la proprietà invariantiva della divisione è la proprietà che rende possibile la semplificazione di numeratore e denominatore di una frazione (quando essi hanno un multiplo in comune). Per esempio, la frazione $\frac{12}{10}$ è del tutto equivalente alla divisione $12 : 10$; se applichiamo la proprietà invariantiva - dividendo sia il divisore che il dividendo per 2 - la divisione diventa $6:5$, cioè la frazione $\frac{6}{5}$. Questo è esattamente quello che avremmo ottenuto semplificando per $2$ il numeratore e il denominatore della frazione da cui siamo partiti.