Disequazioni parametriche di secondo grado: risoluzione

Una disequazione parametrica o letterale di secondo grado è una disequazione in una incognita, di solito $x$, che coinvolge un polinomio di secondo grado in cui, oltre ad $x$, compaiono altre lettere: queste vengono dette parametri. Una disequazione letterale di secondo grado si presenta quindi in uno dei quattro seguenti modi$$ \begin{array}{c} A Ax^2 + B x + C < 0 \\ A x^2 + B x + C \leq 0 \\ A x^2 + B x + C > 0 \\ A x^2 + B x + C \geq 0 \end{array}$$Quelli che normalmente sarebbero i coefficienti numerici del polinomio, $A$, $B$ e $C$, in una disequazione parametrica contengono non solo una parte numerica ma possono anche contenere una parte letterale: si tratta dunque di monomi. Ad ogni modo, li chiameremo sempre coefficienti.

La risoluzione di una disequazione parametrica di secondo grado è sempre piuttosto complicata, dato che unisce tutte le difficoltà di un’equazione parametrica con quelle che si incontrano nel risolvere una disequazione di secondo grado: è dunque importante conoscere bene come si affrontano questi problemi. Di fondamentale importanza è la risoluzione dell’equazione associata: se la disequazione si presenta come una di quelle precedenti, l’equazione ad essa associata è $A x^2 + B x + C = 0$. Possiamo ricapitolare un procedimento di risoluzione di una disequazione parametrica di secondo grado nei seguenti punti: 

1. Stabilire se esistono dei valori dei parametri per i quali i coefficienti perdono di significato: questi valori verranno esclusi dalla nostra indagine. Tutti questi valori per cui i coefficienti non sono definiti costituiscono un insieme che chiamiamo $\mathcal{E}$. 
2. Riordinare la disequazione, mediante passaggi algebrici, di modo che compaia in una delle quattro forme precedentemente illustrate. Mettere bene in evidenza i coefficienti $A$, $B$ e $C$. 
3. Stabilirie se e per quali valori dei parametri il coefficiente $A$ di $x^2$ si annulli. Il coefficiente $A$ del monomio in $x$ di secondo grado viene detto coefficiente direttore. Questi casi, in cui il coefficiente direttore si annulla, vanno trattati separatamente, dato che l’equazione scende di grado: siamo ora di fronte ad una disequazione di primo grado. Si consideri ogni caso singolarmente e si risolva ciascuna disequazione separatamente: notare che queste non sono parametriche, in quanto abbiamo sostituito ai parametri dei valori specifici, e ora al posto di coefficiente monomiali abbiamo solo coefficienti numerici. D’ora in avanti, considereremo sempre valori dei parametri fuori da $\mathcal{E}$ e per cui il coefficiente direttore non si annulli. 
4. Studiare il segno del coefficiente direttore $A$. Avendo escluso i valori dei parametri per cui $A = 0$, rimangono solo due possibilità: o $A>0$ o $A<0$. Raggruppiamo i valori dei parametri per cui $A>0$ o $A<0$ in due insiemi distinti. 
5. Studiare il segno del $\Delta$ dell’equazione associata alla disequazione. Ricordiamo che $\Delta = B^2 - 4 AC$. Dividiamo i valori dei parametri in tre insiemi: rispettivamente, l’insieme dei valori dei parametri per cui $\Delta >0$, per cui $\Delta = 0$ e per cui $\Delta <0$. 
6. Si consiglia di riassumere le condizioni sui parametri e i conseguenti segni di $\Delta $ ed $A$ ottenuti ai punti 4. e 5. in un unico specchietto: questo agevolerà enormemente il trovare la soluzione. 
7. Per i valori dei parametri per cui $\Delta = 0$, risolvere l’equazione associata, che ha una sola soluzione (dipendente da parametri) che indichiamo con $x_0$, e varrà $x_0= \frac{-B}{2A}$. Allo stesso modo, per i valori dei parametri per cui $\Delta > 0$, l’equazione associata avrà due soluzioni, $x_+$ e $x_-$ date dalla famosa formula di risoluzione$$x_{\pm} = \frac{-B \pm \sqrt{\Delta}}{2 A}$$ 
8. Seguire un ragionamento analogo a quello di una semplice disequazione di secondo grado, tenendo conto di tutte le specificazioni ottenute sino a questo punto. Possiamo riassumere le soluzioni nella seguente tabella:
   

   	$$\Delta > 0 $$	$$\Delta = 0 $$	$$\Delta < 0 $$
   $$Ax^2 + Bx + C > 0$$	$$\begin{cases}x>x_+ \vee x<x_- & \text{ se } A>0\\x_- < x < x_+ & \text{ se } A<0\end{cases}$$	$$\begin{cases}x \neq x_0 & \text{ se } A>0\\\text{impossibile }& \text{ se } A<0\end{cases}$$	$$\begin{cases}\forall x \in \mathbb{R} & \text{ se } A>0\\ \text{impossibile }& \text{ se } A<0\end{cases}$$
   $$Ax^2 + Bx + C \geq 0$$	$$\begin{cases}x\geq x_+ \vee x\leq x_- & \text{ se } A>0\\x_- \leq x \leq x_+ & \text{ se } A<0\end{cases}$$	$$\begin{cases} \forall x \in \mathbb{R} & \text{ se } A>0\\ x = x_0 & \text{ se } A<0\end{cases}$$	$$\begin{cases}\forall x \in \mathbb{R} & \text{ se } A>0\\ \text{impossibile }& \text{ se } A<0\end{cases}$$
   $$Ax^2 + Bx + C <0$$	$$\begin{cases} x_- < x < x_+ & \text{ se } A>0\\ x>x_+ \vee x<x_- & \text{ se } A<0 \end{cases}$$	$$\begin{cases} \text{impossibile }& \text{ se } A>0 \\ x \neq x_0 & \text{ se } A<0 \end{cases}$$	$$\begin{cases} \text{impossibile }& \text{ se } A>0 \\ \forall x \in \mathbb{R} & \text{ se } A<0 \end{cases}$$
   $$Ax^2 + Bx + C \leq 0$$	$$\begin{cases}x_- \leq x \leq x_+ & \text{ se } A>0\\x \geq x_+ \vee x \leq x_- & \text{ se } A<0\end{cases}$$	$$\begin{cases}x = x_0 & \text{ se } A>0 \\\forall x \in \mathbb{R} & \text{ se } A<0\\\end{cases}$$	$$\begin{cases}\text{impossibile }& \text{ se } A>0 \\\forall x \in \mathbb{R} & \text{ se } A<0\end{cases}$$

Notare che le disequazioni che coinvolgono $\Delta$ e $A$, che abbiamo incontrato nello studio del loro segno, pongono delle condizioni sui valori dei parametri: per ciascuna di queste condizioni, si otterrà una soluzione differente. Per questo motivo, si consiglia di essere molto chiari nella risoluzione degli esercizi, e, quando si è pervenuti alla soluzione, di evidenziare tutto ciò che si è scoperto in uno specchietto riassuntivo.

Se la discussione sembra piuttosto complicata, un esempio chiarià sicuramente ogni dubbio.

Si chiede di torvare la soluzione della disequazione parametrica di secondo grado$$(2a^2 - 1) x^2 - 2 (a-1) x -2 \leq 0 $$Come si vede, oltre all’incognita $x$ compare il parametro $a$. Procediamo seguendo i punti stabiliti sopra.

1. I parametri non compaiono in forme algebriche che potrebbero perdere di significato per qualche loro valore: non ci sono frazioni il cui denominatore potrebbe annullarsi, logaritmi il cui argomento potrebbe essere negativo, e così via. Tutti i valori del parametro $a$ saranno accettabili.
2. La disequazione compare già in una delle forme elencate all’inizio, quindi non dobbiamo preoccuparci di riordinarla. I coefficienti sono $A = 2a^2 -1$, $B= -2(a-1)$ e $C = -2$.
3. Cerchiamo di annullare il coefficiente direttore $A$: imponendo $A=0$, otteniamo l’equazione$2a^2 -1 =0$, che ha per soluzione $a = \pm \frac{\sqrt{2}}{2}$. Per ciascuno di questi valori particolari, otteniamo una disequazione (NON parametrica) di primo grado, di cui riportiamo la soluzione:##KATEX##\begin{aligned} a = \frac{\sqrt{2}}{2} & \Rightarrow x \geq - \frac{2}{\sqrt{2} -2 } \\ a = -\frac{\sqrt{2}}{2} & \Rightarrow x \geq \frac{2}{\sqrt{2} +2 }\end{aligned}##KATEX## 
4. Dobbiamo studiare il segno di $A$, in funzione del parametro $a$: si tratta di risolvere una disequazione di secondo grado (in $a$). Senza riportare tutti i passaggi, si determina facilmente che $A >0$ se $a > \frac{\sqrt{2}}{2}$ o $a < -\frac{\sqrt{2}}{2}$, e viceversa $A<0$ se $ -\frac{\sqrt{2}}{2} < a < \frac{\sqrt{2}}{2}$. Iniziamo a riportare queste informazioni in un piccolo diagramma: 
   
5. Il $\Delta$ della disequazione è pari a$$ \Delta = \left(- 2(a-1) \right)^2 - 4 \cdot (2a^2 -1) \cdot (-2) = \dots = 20a^2 - 8 a -4$$studiare il segno di questa espressione significa risolvere alcune disequazioni (in $a$). Dopo alcuni brevi calcoli si giunge ai seguenti risultati:##KATEX##\begin{aligned} \Delta = 0 &\text{ per } a = \frac{1\pm \sqrt{6}}{5} \\ \Delta > 0 & \text{ per } a > \frac{1 + \sqrt{6}}{5} \vee a < \frac{1 - \sqrt{6}}{5} \\ \Delta < 0 & \text{ per } \frac{1 - \sqrt{6}}{5} < a < \frac{1 + \sqrt{6}}{5} \end{aligned}##KATEX##
6. Riassumiamo questi risultati sul segno di $A$ e di $\Delta$ nello stesso diagramma che avevamo iniziato a tracciare in precedenza:
   
7. Nei casi in cui $\Delta = 0$, la soluzione dell’equazione associata è $x_0 = \frac{a-1}{2a^2 -1}$, mentre per $\Delta > 0$ abbiamo le due soluzioni $x_{\pm} = \frac{a-1 \pm \sqrt{5a^2 -2a -1}}{2a^2 -1}$. Facciamo presente che nel calcolo di queste soluzioni è possibile usare la formula ridotta, dato che in $B$ compare un fattore $2$: non importa che la disequazione o l’equazione siano parametriche. Possiamo anche calcolare normalmente le soluzioni e poi estrarre un fattore $2$ dalla radice.
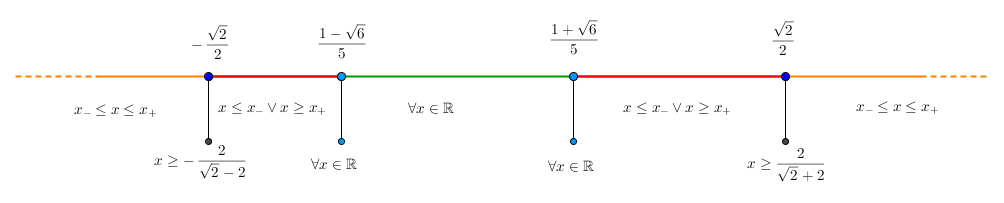
8. Con tutte queste informazioni, possiamo ricavare le soluzioni della disequazione di partenza, in dipendenza dei valori assunti dal parametro $a$: riassumiamole nello specchietto seguente, tenendo presente tutte le considerazioni fatte sino a questo punto.
   1. Per $a < -\frac{\sqrt{2}}{2} $ oppure $ a > \frac{\sqrt{2}}{2}$, abbiamo come soluzione l’intervallo chiuso e limitato $x- \leq x \leq x_+$.
   2. Per $a = -\frac{\sqrt{2}}{2}$, abbiamo la soluzione $x \geq -\frac{2}{\sqrt{2} - 2}$.
   3. Per $ -\frac{\sqrt{2}}{2} < a < \frac{1 - \sqrt{6}}{5}$ oppure $ \frac{1 + \sqrt{6}}{5} < a < \frac{\sqrt{2}}{2} $, la soluzione è rappresentata da due intervalli illimitati, poiché sono accettabili tutti i valori $x \leq x_-$ oppure quelli $x \geq x_+$.
   4. Per $a = \frac{1 \pm \sqrt{6}}{5}$, la soluzione è l'intero asse reale: la disequazione è soddisfatta $\forall x \in \mathbb{R}$. Facciamo notare che se la disequazione di partenza fosse stata stretta (cioè $(2a^2 - 1) x^2 - 2 (a-1) x -2 > 0$), in questi due casi si sarebbe dovuto escludere il valore $x_0$ dalla soluzione.
   5. Anche per $\frac{1 - \sqrt{6}}{5} < a < \frac{1 + \sqrt{6}}{5}$ vanno bene tutti i valori reali per l’incognita $x$: la soluzione è rappresentata da tutto l’asse reale.
   6. Per $a = \frac{\sqrt{2}}{2}$ la soluzione è data dalla semiretta $x \geq \frac{2}{\sqrt{2} + 2}$.