L’applicazione della trigonometria ai triangoli rettangoli ha numerose conseguenze in Geometria. Tra i teoremi più importanti che possiamo ricordare, c’è il teorema della corda, che permette di legare in maniera molto elegante la misura del diametro di una circonferenza con la misura di una sua corda qualsiasi.
Questo teorema viene utilizzato negli esercizi per ricavare la lunghezza di una corda di una circonferenza a partire dalla lunghezza del suo raggio e dall’ampiezza dell’angolo che sottende tale corda. A volte, invece, il teorema viene utilizzato “al contrario”: a partire dalla lunghezza di una corda e dall’ampiezza di un angolo alla circonferenza che la sottende, si determina direttamente il diametro della circonferenza considerata.
TEOREMA (della corda): Consideriamo una circonferenza di raggio $r$ e una sua corda $AB$. Allora la lunghezza $\overline{AB}$ della corda è uguale al prodotto tra la lunghezza del diametro della circonferenza e il seno di un qualunque angolo alla circonferenza $\alpha$ che sottende la corda $AB$. In formule: $$\overline{AB} = \sin \alpha \cdot 2r$$

Dimostrazione. Suddividiamo l’analisi in due casi:
- Se la corda $AB$ è un diametro, allora sappiamo che un qualsiasi angolo alla circonferenza $\alpha$ che sottende $AB$ è retto. Siccome $\sin \alpha = \sin \frac{\pi}{2} = 1$, allora il teorema è valido: $$\overline{AB} = 2r = 1 \cdot 2r = \sin \alpha \cdot 2r.$$

- Se la corda $AB$ non è un diametro, tracciamo invece il diametro $AM$. L’angolo $\widehat{ABM}$ è retto: possiamo quindi esprimere $\overline{AB}$ in funzione della lunghezza $\overline{AM} = 2r$ e dell’angolo $\widehat{AMB}$, utilizzando le funzioni trigonometriche: $$\overline{AB} = \overline{AM} \cdot \sin ( \widehat{AMB} ).$$
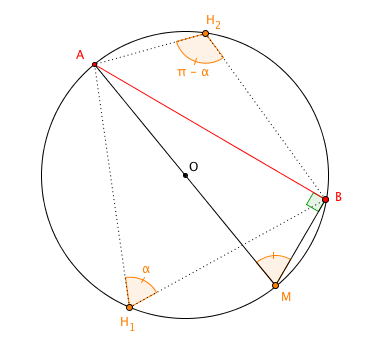
Notiamo i seguenti fatti.
- Preso un qualunque punto $H_1$ sull’arco $\overset{\frown}{AB}$ su cui giace $M$, si ha che $\widehat{AH_1B} = \widehat{AMB}$. Questo accade perché gli angoli alla circonferenza considerati sottendono lo stesso arco.
- Preso un qualunque altro punto $H_2$ sull’arco $\overset{\frown}{AB}$ su cui non giace $M$, abbiamo che $\widehat{AH_2B} = \pi - \widehat{AH_1B}$. Questo accade perché il quadrilatero $AH_1BH_2$ - comunque scelti $H_1$ e $H_2$ - è inscritto in una circonferenza, e quindi gli angoli opposti $\widehat{AH_2B}$ e $\widehat{AH_1B}$ sono supplementari.
La prima osservazione ci garantisce che possiamo scegliere un qualsiasi angolo alla circonferenza $\alpha = \widehat{AH_1B}$ su $\overset{\frown}{AB}$, dalla parte di $M$, e la relazione $\overline{AB} = \sin \alpha \cdot 2r$ sarà valida; infatti: $$\sin \alpha = \sin ( \widehat{AH_1B} ) = \sin ( \widehat{AMB} ).$$
D’altra parte, grazie alla seconda osservazione e all’utilizzo delle formule degli archi associati, possiamo scrivere la seguente catena di uguaglianze: $$\sin ( \widehat{AH_2B} ) = \sin ( \pi - \widehat{AH_1B} ) = \sin ( \widehat{AH_1B} ) = \sin \alpha.$$Questo ci garantisce che la formula del teorema è comunque vera, anche se scegliamo un angolo alla circonferenza $\widehat{AH_2B}$ con vertice sull’arco $\overset{\frown}{AB}$ dove non giace $M$.
Con questa analisi, abbiamo dunque mostrato che la formula $\overline{AB} = 2r \sin \alpha$ è valida per qualunque scelta di $AB$ e di $\alpha$: il teorema è quindi dimostrato.