Problema 2
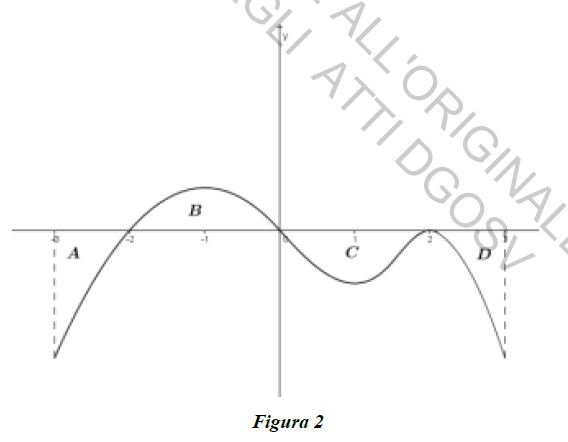
La funzione derivabile $y = f(x)$ ha, per $x \in [-3, 3]$, il grafico $\Gamma$, disegnato in figura 2. $\Gamma$ presenta tangenti orizzontali per $x = -1, x=1, x=2$. Le aree delle regioni $A$, $B$, $C$ e $D$ sono rispettivamente $2$, $3$, $3$ e $1$. Sia $g(x)$ una primitiva di $f(x)$ tale che $g(3) = -5$.
- Nel caso $f(x)$ fosse esprimibile come un polinomio, quale potrebbe essere il suo grado minimo? Illustra il ragionamento seguito.
- Individua i valori di $x \in [-3, 3]$, per cui $g(x)$ ha un massimo relativo e determina i valori di $x$ per i quali $g(x)$ volge la concavità verso l’alto.
- Calcola $g(0)$ e, se esiste, il $\displaystyle{\lim_{x \to 0} \frac{1+g(x)}{2x}}$.
- Sia $h(x) = 3 \cdot f(2x+1)$, determina il valore di $\displaystyle \int_{-2}^1 h(x)dx$.
Soluzione
Dal grafico si vede che $f(x)$ è una funzione integrabile sull’intervallo $[-3, 3]$. Per il teorema fondamentale del calcolo integrale, la funzione integrale $$\tilde{g}(x) := \int_{-3}^x f(t) dt$$è definita in tutto l’intervallo considerato ed è una primitiva della funzione $f(x)$.
Osservando la figura e i dati forniti e ricordando che il valore dell’integrale definito esprime l’area con segno sottesa dal grafico della funzione otteniamo che: ##KATEX##\begin{aligned} \int_{-3}^{-2}f(x)dx & = -2 & \int_{-2}^{0}f(x)dx & = 3 \\ \int_{0}^{2}f(x)dx & = -3 & \int_{2}^{3}f(x)dx & = -1 \end{aligned}##KATEX##La funzione $\tilde{g}$ soddisfa quindi queste condizioni: ##KATEX##\begin{aligned} \tilde{g}(-2) & = -2 & \tilde{g}(0) & = -2 +3 = 1 \\ \tilde{g}(2) & = -2 + 3 -3 = -2 & \tilde{g}(3) & = -2+3-3-1=-3 \end{aligned}##KATEX##Ogni primitiva $G(x)$ di $f(x)$ differisce da $\tilde{g}(x)$ di una costante additiva; volendo noi una primitiva $g(x)$ tale che $g(3) = -5$, otteniamo $$g(x) = \tilde{g}(x) - 2 = \int_{-3}^x f(t) dt - 2.$$
- Come espresso dai dati, la funzione $f(x)$ ammette nell’intervallo $[-3, 3]$ solamente tre punti con tangente orizzontale: la derivata di $f(x)$ in questi punti sarà nulla. Se $f(x)$ è un polinomio, anche la derivata $f’(x)$ lo sarà. Dato che la derivata si deve annullare in $x=-1$, $x=1$ e $x=2$, per il teorema di Ruffini $f’(x)$ sarà necessariamente della forma $$f’(x) = (x+1)(x-1)(x-2)p(x)$$ dove $p(x)$ è un polinomio opportuno. Il grado minimo di $f’(x)$ si realizza quando $p(x)$ è una costante, cioè un polinomio di grado $0$. Integrando un polinomio di grado $3$ otteniamo sempre un polinomio di grado $4$: questo è il grado minimo di $f(x)$.
- Eventuali massimi e minimi di $g(x)$ vanno ricercati tra gli zeri di $f(x)$, che è la sua derivata. Dal grafico si deduce che tali zeri sono in corrispondenza di $x=-2$, $x=0$, $x=2$. Studiando il segno di $f(x)$, inoltre, segue che $x=-2$ è un punto di minimo per $g(x)$ ($f(x)$ è negativa prima di tale punto e positiva dopo), $x=0$ è un punto di massimo per $g(x)$ ($f(x)$ è positiva prima di tale punto e negativa dopo), mentre $x=2$ è un punto di flesso a tangente orizzontale per $g(x)$ (essendo $f(x)$ negativa sia prima sia dopo tale punto). Da queste considerazioni otteniamo che $x=0$ è un punto di massimo relativo (anzi assoluto!).
La concavità di $g(x)$ è determinata dal segno della sua derivata seconda, cioè dal segno di $f’(x)$. Dal grafico, osservando la monotonia di $f(x)$, si evince che ##KATEX##\begin{aligned} f’(x) > 0 & \qquad \text{ quando }x \in (-3, -1) \vee x \in (1, 2) \\ f’(x) < 0 & \qquad \text{ quando }x \in (-1, 1) \vee x \in (2, 3) \end{aligned}##KATEX##La concavità di $g(x)$ è rivolta verso l’alto quando $f’(x) > 0$, cioè quando $x \in (-3, -1) \vee x \in (1, 2)$. - Per definizione, $g(x) = \tilde{g}(x) - 2$ e per quanto premesso abbiamo $$g(0) = \tilde{g}(0) - 2 = 1 - 2 = -1$$Il limite proposto è una forma di indecisione: infatti, sostituendo $x=0$ al numeratore e al denominatore, otteniamo la forma $\left [ \frac{0}{0} \right ]$. Dato che sia il numeratore che il denominatore sono derivabili, possiamo applicare il teorema di de l’Hôpital ottenendo: $$\lim_{x \to 0} \frac{1+g(x)}{2x} = \lim_{x \to 0} \frac{g’(x)}{2} = \lim_{x \to 0} \frac{f(x)}{2} = \frac{1}{2} \lim_{x \to 0} f(x)$$Siccome $f(x)$ è continua in $x=0$ (come si vede dal grafico) allora $\displaystyle \lim_{x \to 0} f(x) = 0$. In conclusione, il limite che vogliamo calcolare esiste e vale $0$.
- L’integrale che vogliamo determinare può essere risolto mediante la sostituzione $t = 2x+1$. Gli estremi di integrazione cambiano in questo modo: $$x=-2 \quad \leadsto \quad t=-3, \qquad \qquad x=1 \quad \leadsto \quad t=3$$I differenziali sono legati dalla seguente relazione: $$t = 2x+1 \quad \leadsto \quad dt = 2dx.$$Con questo espediente, il nostro integrale diventa: ##KATEX##\begin{aligned} \int_{-2}^1 h(x)dx & = \int_{-2}^1 ( 3 \cdot f(2x+1) ) dx = 3 \cdot \int_{-2}^1 f(2x+1) dx = \\ & = 3 \cdot \int_{-3}^3 f(t) \frac{1}{2} dt = \frac{3}{2} \tilde{g}(3) \end{aligned}##KATEX##Come calcolato all’inizio $\tilde{g}(3) = -3$ e quindi l’integrale richiesto vale $-\frac{9}{2}$.